Методические указания к проведению лекционного занятия

Тема № 7.14. Статистическое оценивание и проверка гипотез

План:

1. Оценки параметров распределения

2. Проверка статистических гипотез

1. Оценки параметров распределения

Изучая выборку, мы делаем вывод обо всех объектах генеральной совокупности. Чтобы результаты исследования были более точными, необходимо провести несколько исследований: изучить несколько выборок.

Для исследования, изучающего число неправильных соединений за 1 мин. между абонентами на телефонной станции, найдем среднее число неправильных соединений, дисперсию и среднее квадратическое отклонение числа неправильных соединений.

Таблица статистического распределения имеет вид:

Варианты, xi	0	1	2	3	4	6	7
Относ. частоты,

=0· +1· +2· +3· +4· +6· +7· =2 =2,6. Среднее число неправильных соединений равно 2,6.

S²=0· +1· +4· +9· +16· +36· +49· -2,6²= -6,76=12,2-6,76=5,44.

σ= =

В этом случае найдено среднее число неправильных соединений для данной выборки, дисперсия и среднее квадратическое отклонение.

Если сделать еще одну выборку, то среднее значение уже возможно изменится, а также изменятся дисперсия и среднее квадратическое отклонение.

«Истинное» значение математического ожидания, дисперсии и среднего квадратического отклонения генеральной совокупности называются параметрами распределения генеральной совокупности.

Для того, чтобы оценки неизвестных параметров распределения генеральной совокупности были более точными, они должны удовлетворять следующим требованиям:

1. Математическое ожидание оценки параметра по всем возможным выборкам одинакового объема должно равняться истинному значению определяемого параметра. В этом случае оценку называют несмещенной.

2. При увеличении объема выборки оценка должна сходиться по вероятности к истинному значению параметра. В этом случае оценку называют состоятельной.

Распределение среднего значения выборки

Среднее выборочное является случайной величиной, значение которой зависит от того, какие значения приняли варианты x_i. Обозначим среднее выборочное за a, а дисперсию выборки - σ². Найдем математическое ожидание и дисперсию среднего выборочного. M =M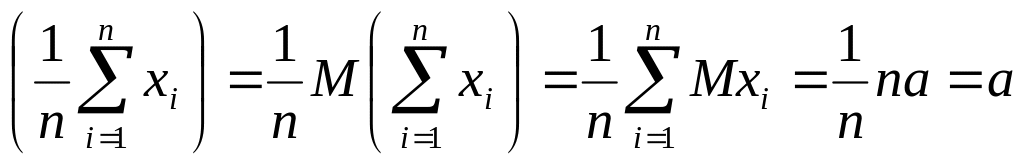

D =D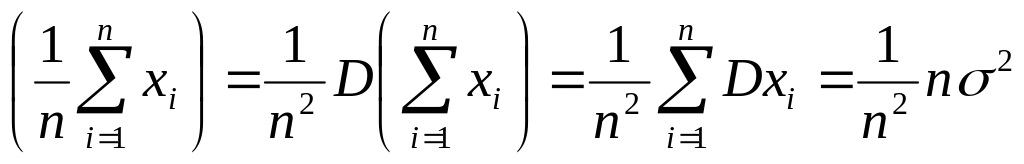 . Таким образом, математическое ожидание среднего выборочного равно среднему выборочному, а дисперсия в n раз меньше. То есть чем больше выборок будет исследовано, тем меньше будет разброс. Среднее выборочное является несмещенной и состоятельной оценкой.

Распределение выборочной дисперсии

Выборочная дисперсия является смещенной оценкой. Какой бы ни была с.в. ξ, порождающая выборку, MS²= . «Смещение» оценки происходит из-за того, что отклонение выборочных значений отсчитывается не от математического ожидания с.в. ξ, а от среднего выборочного. Чтобы получить несмещенную оценку дисперсии s², необходимо дисперсию выборки S² умножить на , s²= S². В этом случае, M =M = · .

Интервальные оценки параметров распределения.

Доверительный интервал для математического ожидания, если среднее квадратическое отклонение генеральной совокупности известно.

Пусть a=M_ξ, σ – среднее квадратическое отклонение ξ, n – объем выборки, тогда математическое ожидание генеральной совокупности покрывает интервал , где β – уровень доверия, k_β – значение нормального распределения (см. табл. 5)

Доверительный интервал для математического ожидания, если среднее квадратическое отклонение генеральной совокупности неизвестно.

, где s – несмещенное среднее квадратическое отклонение, s= , t_n,β – коэффициент Стьюдента (см. табл. 6).

Доверительный интервал для среднего квадратического отклонения генеральной совокупности.

, где значения q_n,β (см. таблицу 7)

Пример. Найти доверительный интервал c надежностью 0,95 для оценки математического ожидания нормально распределенной с.в. x, если известны ее среднее квадратическое отклонение σ=4, среднее выборочное =16 и объем выборки n=16.

Решение. . По условию задачи =16, n=16, β=0,95, σ=4, значение нормального распределения k_0,95=1,96. Тогда , то есть

Пример. Из генеральной совокупности извлечена выборка объема n=10 и составлена таблица относительных частот:

Варианты, xi	-1	0	1	2	3	4
Относ. частоты,	0,2	0,1	0,2	0,1	0,2	0,2

Найти доверительный интервал для оценки математического ожидания и среднего квадратического отклонения нормально распределенной с.в. x с уровнем доверия 0,99.

Решение. 1. Поскольку среднее квадратическое отклонение генеральной совокупности неизвестно, то . По условию задачи n=10, β=0,99, значит коэффициент Стьюдента t_9;0,99=3,36.

Найдем среднее выборочное и несмещенное среднее квадратическое отклонение.

=-0,2+0,2+0,2+0,6+0,8=1,6.

Дисперсия выборки S²=0,2+0,2+0,4+1,8+3,2-2,56=5,8-2,56=3,24, тогда несмещенное среднее квадратическое отклонение s= .

,

,

,

2. Среднее квадратическое отклонение находится в интервале: . Значение q_10;0,99=1,08.

,

,

.