Основні показники динамічного ряду

Роки	Кількість викликів	Абсолютний приріст,		Темп приросту,		Темп росту, 
		Базисний	Ланцю-говий	Базисний %	Ланцю-говий, %
1	621	0	––––––	100	––––––	––––
2	943	322	322	151,8	151,8	51,8
3	901	280	-42	145,1	95,5	-4,5
4	891	260	-10	143,5	98,9	-1,1
5	731	110	-160	117,7	82	-18
6	764	143	33	123	104,5	4,5
7	758	137	-6	122,1	199,2	-0,8
8	882	261	126	142	116,3	16,3

Кількість викликів має тенденцію до зростання (малюнок 4.2), разом з цим позитивні та негативні абсолютні прирости чергуються. У зв’язку з цим здійснемо збільшення інтервалів до двох років та обчислимо значення показників динамичного ряду за формулами (7-11), результати розрахунків зведемо в таблицю №5.

Таблиця №5.

Значення показників динамічного ряду для збільшених інтервалів часу

Рік	Кількість викликів	Абсолютний приріст	Темп приросту
1/2		-	-
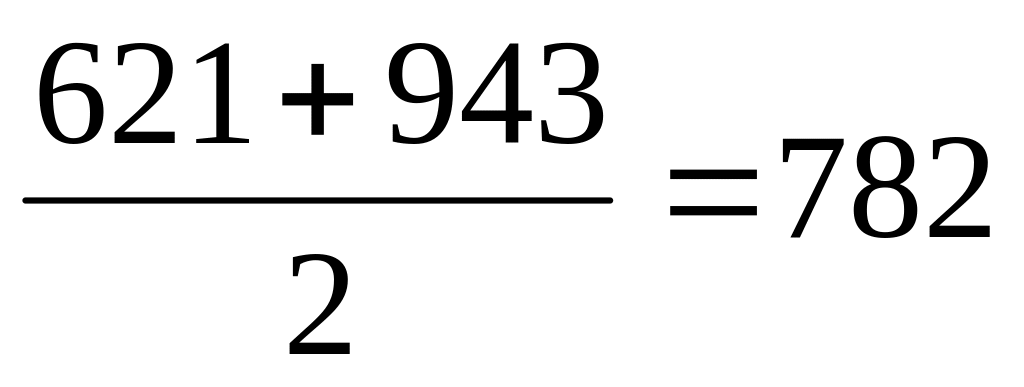
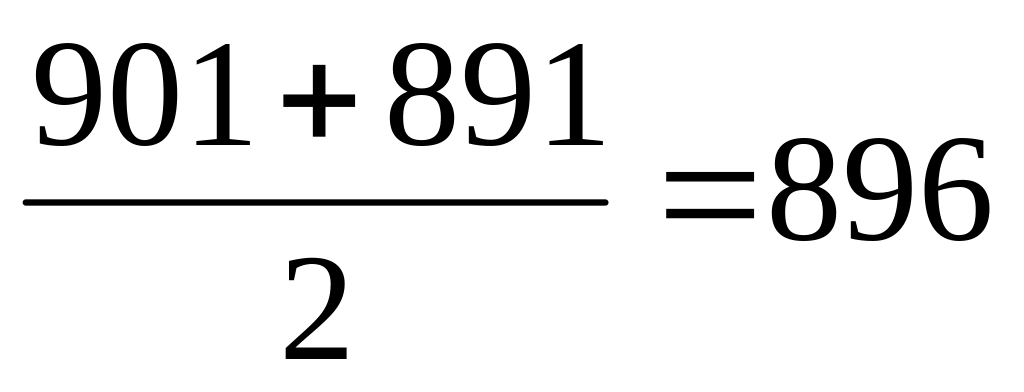
3/4		896-782=114
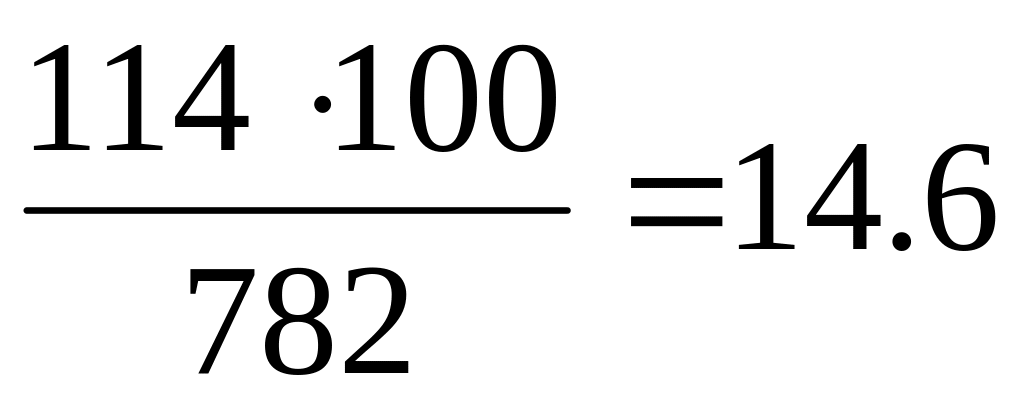
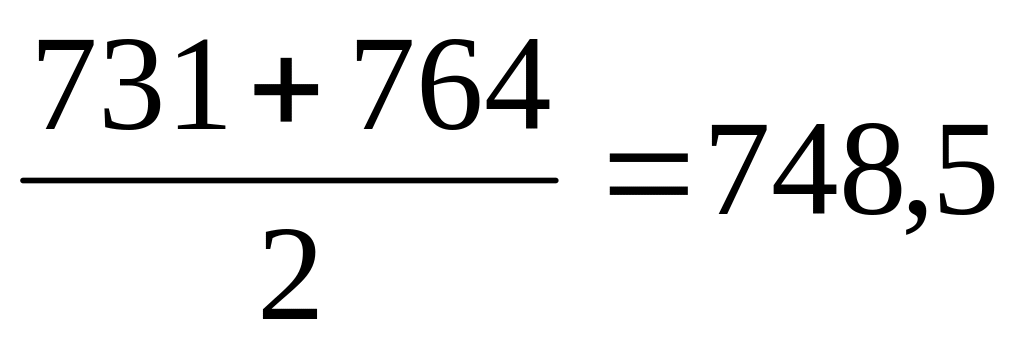
5/6		748,5-896=-147,5
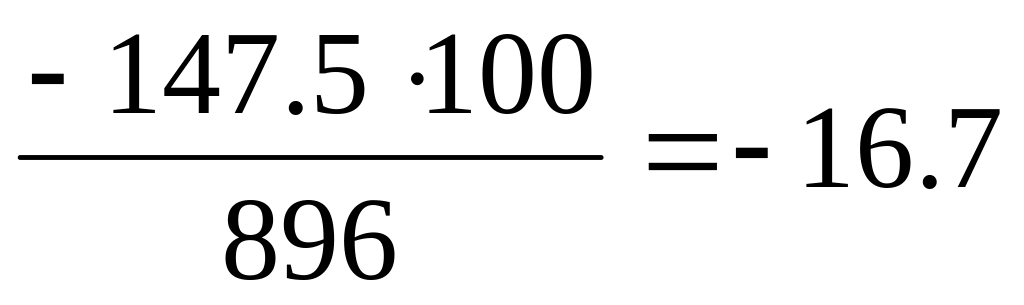
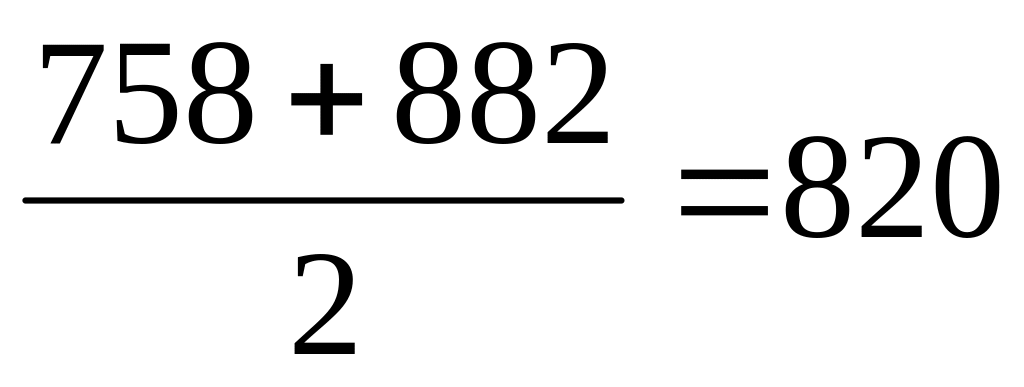
7/8		820-748,5=50,5

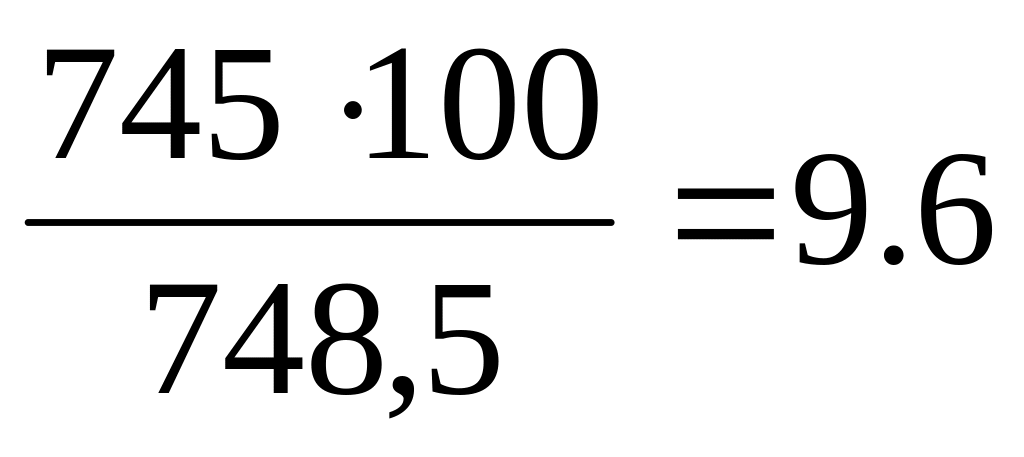
Аналіз значень абсолютных приростів показує, що вони відносно стабільні. Тому динамичний ряд приблизно можна вирівняти за прямою. Для підрахунку необхідних сум складемо розрахункову таблицю №6

Таблиця №6.

Розрахунок показників вирівняного ряду динаміки

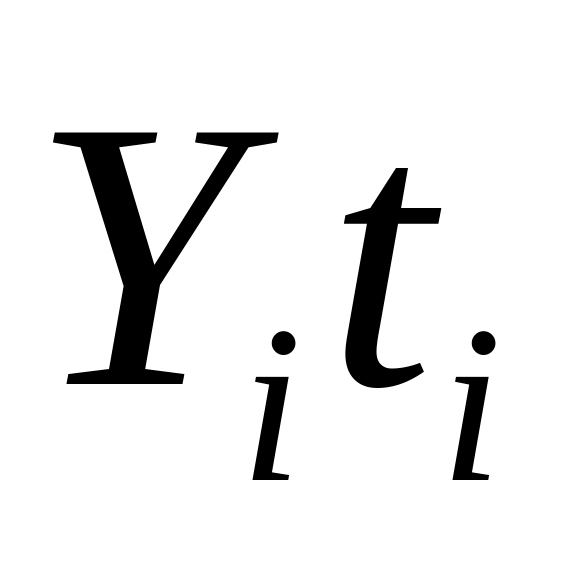
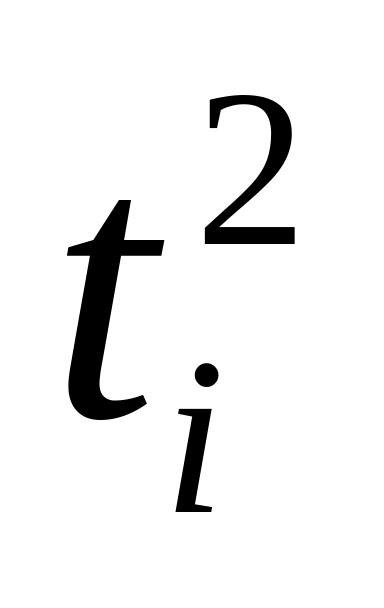
Рік,	Кількість викликів,	Позначений час,			Вирівн. ряд,
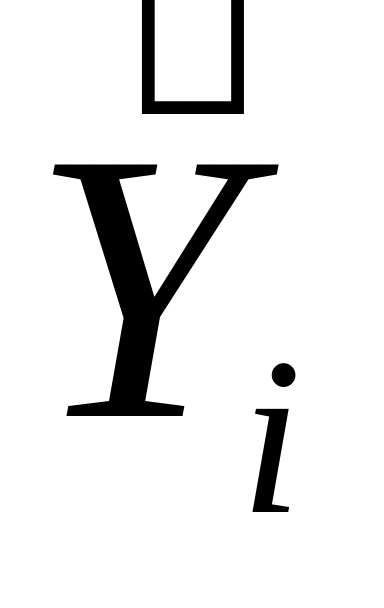
1	621	-7	-4347	49	797,6
2	943	-5	-4715	25	801,5
3	901	-3	-2703	9	805,5
4	891	-1	-891	1	809,4
5	731	1	731	1	813,4
6	764	3	2292	9	817,3
7	758	5	3790	25	821,2
8	882	7	6174	49	825,2
Сума	6491	0	331	168	6491

Підставляючи у формули (18-19) суми з таблиці №6, одержимо:

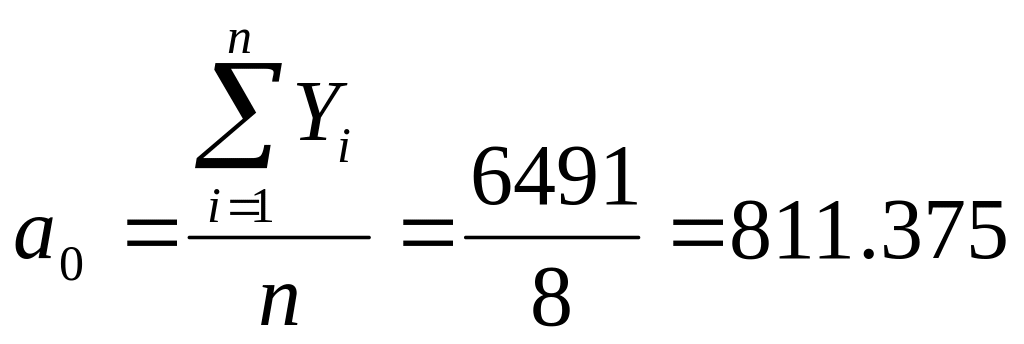
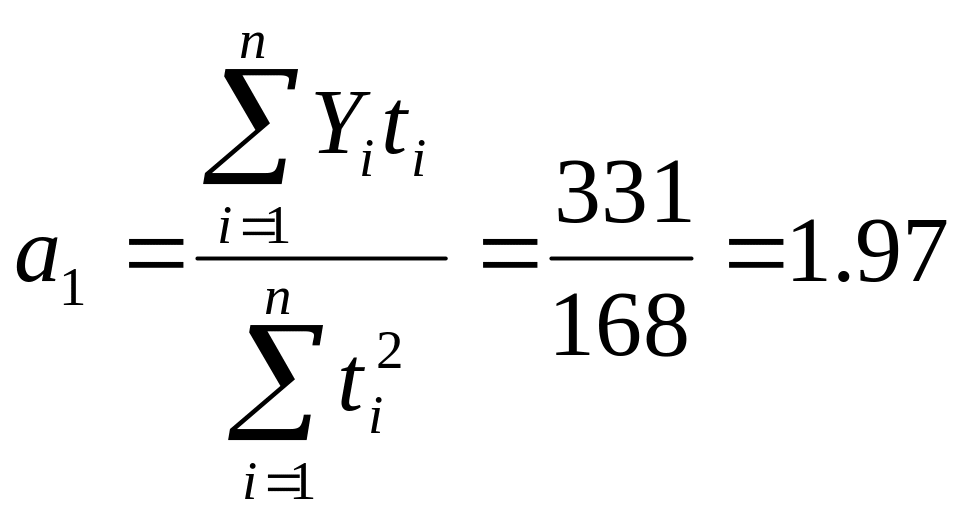
Звідси рівняння початкової прямої буде:

Шляхом підстановки в це рівняння відповідних значень (див. графу 3 таблиці №10) знайдемо вирівняні рівні Y_i. Так для і = 9 одержимо:

Як бачимо з порівняння результатів сум граф 2 і 6 таблиці №10, значення сум та однакові, что свідчить про вірність розрахунків для визначення параметрів a₀ и a₁ рівняння. Розробимо прогноз кількості викликів на найближчий рік:

Таким чином, в наступному році очикується біля 829 викликів. Одержані вирівняні рівні ряду та його прогнозне значення наносимо на графік (малюнок №5).

Середня кількість викликів пожежних підрозділів у добу розраховується на підставі дискретного варіаційного ряду табл. 3.2 гр.4 за формулами:

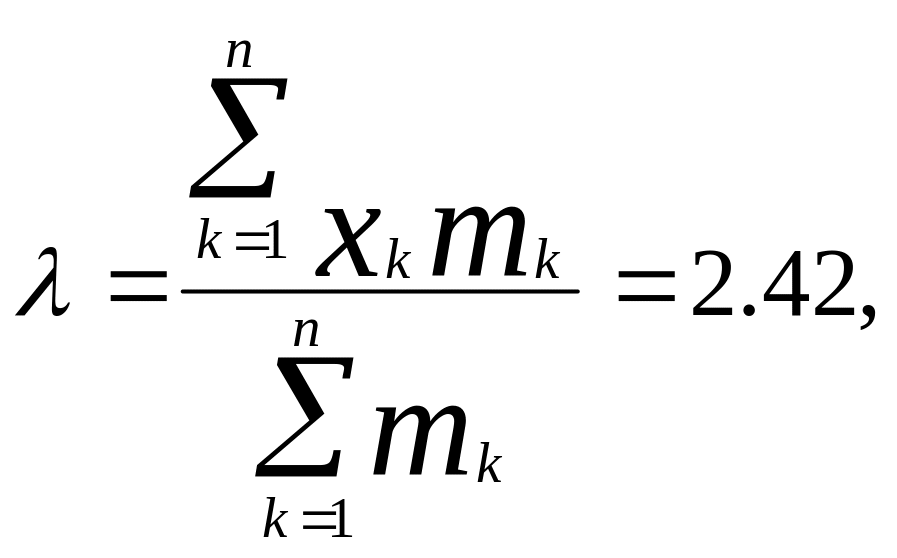(3.19)

де x_k – кількість викликів у добу;

m_k –кількість діб із зазначеною кількістю викликів, або

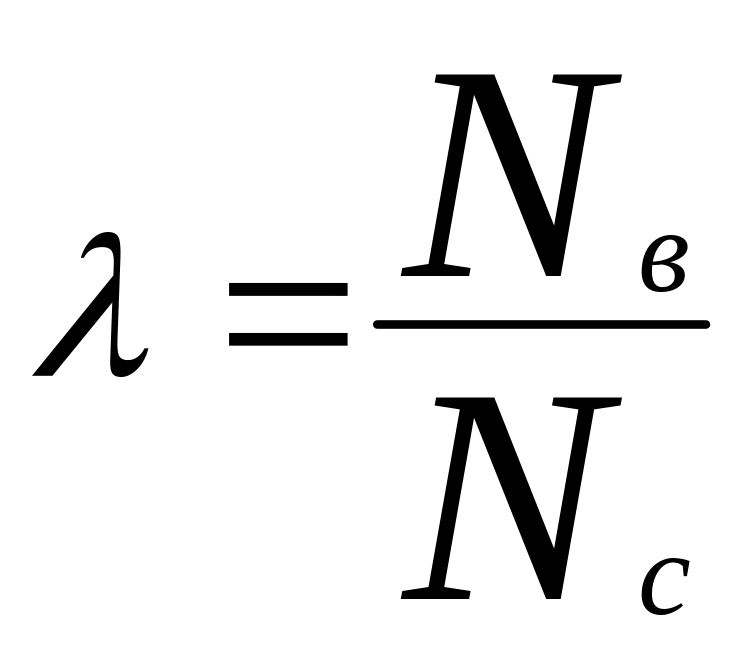, (3.20)

-де N_в – загальна кількість викликів за аналізований період часу;

N_с –кількість діб в даному періоді.

Застосування величини для розрахунку необхідної кількості пожежних автомобілів за допомогою методів теорії масового обслуговування можливо лише тоді, коли реальні потоки викликів пожежних підрозділів у місті досить добре описується законом Пуассона. Для перевірки гіпотези про пуассонівский характер потоків викликів пожежних підрозділів у місті необхідно за допомогою відповідних критеріїв згоди, шляхом складання графіків розподілу оцінити ступінь близькості отриманих емпіричних розподілів до передбачуваного теоретичного (до розподілу Пуассона). Теоретичний розподіл кількості діб з тією або іншою кількістю викликів пожежних підрозділів за аналізований період часу можна знайти за формулою:

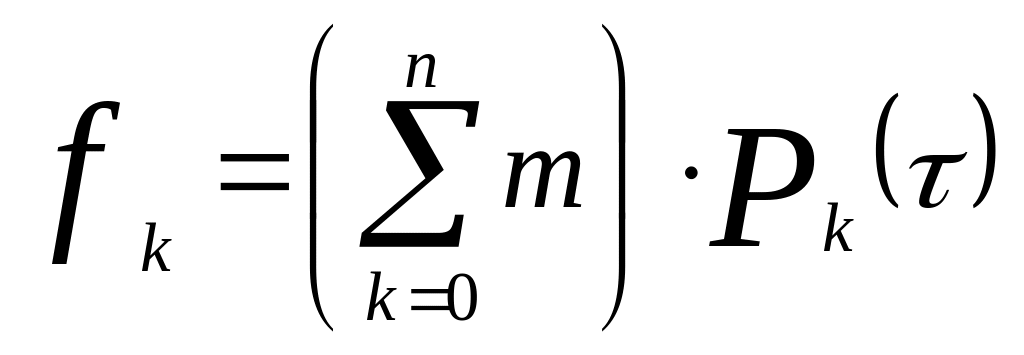, (3.21)

де - теоретична імовірність тієї або іншої кількості викликів к=0,1,2,3…n, на інтервалі часу доба;

(3.22)

Співставлення емпіричного розподілу кількості діб m_k і теоретичного розподілу здійснюється за допомогою критерію Романовского, що дозволяє визначити, чи є наявними або випадковими розбіжності між розподіленнями або вони закономірні:

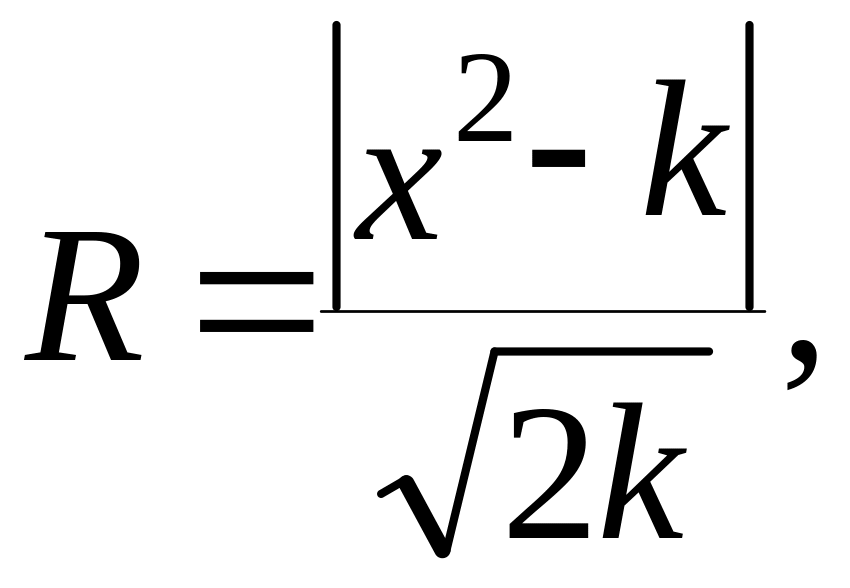(3,23)

де k=n-2 – число ступенів свободи;

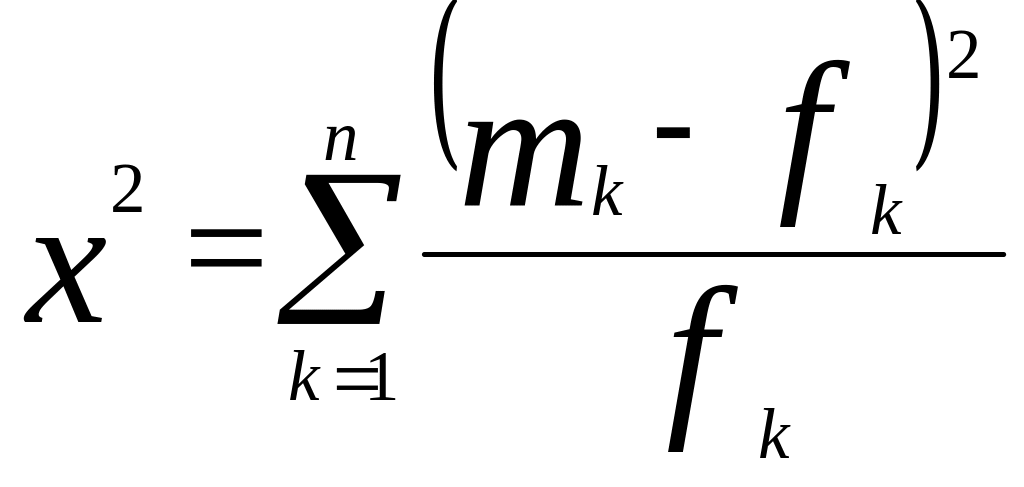- критерій Пірсона. (3.24)

Якщо величина критерію Романовського менше 3, то розбіжність між емпіричними і теоретичними розподілами несуттєва, і прийнятий закон розподілу може служити моделлю емпіричних даних.

Надано (таблиця 3.7) розподіл викликів пожежних підрозділів за добами року. Потрібно графічно зобразити даний розподіл, визначити середню кількість викликів за добу, побудувати математичну модель потоку викликів і перевірити її відповідність емпіричним даним.

Таблиця 7

Кількість викликів за добу	0	1	2	3	4	5	6	7
Емпірична частота (кількість діб із заз-наченою кількістю викликів) mk	33	77	95	77	47	23	10	3
Теоретична частота fk	32.5	76.65	94.9	76.75	47.45	21.9	9.21	3.14

З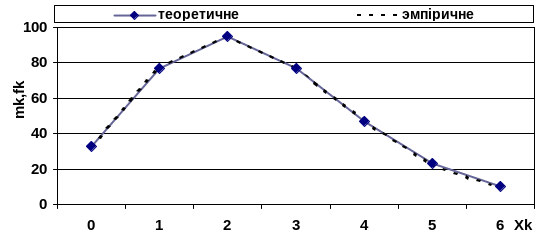 начення f_k проставляється в таблицю 3.7 після відповідних розрахунків. Будуємо полігон емпіричного розподілу кількості викликів (рисунок 3.3).

Рисунок 3 Розподіл кількості викликів на інтервалі

часу доба.

Знайдемо середню кількість викликів за добу. Для цього скористаємося формулою (4.19).

Знаходимо імовірність того, що на інтервалі часу доба відбудеться одночасно k викликів. Знаючи величини імовірностей, визначимо відповідне значення теоретичних частот f_к по (3.21). Отримані дані заносимо у вихідну таблицю 3.7 і на графік (малюнок 3.3). Використовуючи критерій Романовського, перевіримо відповідність побудованої математичної моделі потоку викликів емпіричним даним. Насамперед визначимо значення Х². Для цього складемо таблицю 3.8, у яку занесемо емпіричні частоти розподілу і відповідні їм теоретичні дані f_k, знайдені в припущенні, що емпіричний розподіл пуассонівский. Тут же визначимо величину Х².

Таблиця 8

mk	fk		mk-fk	(mk-fk)2
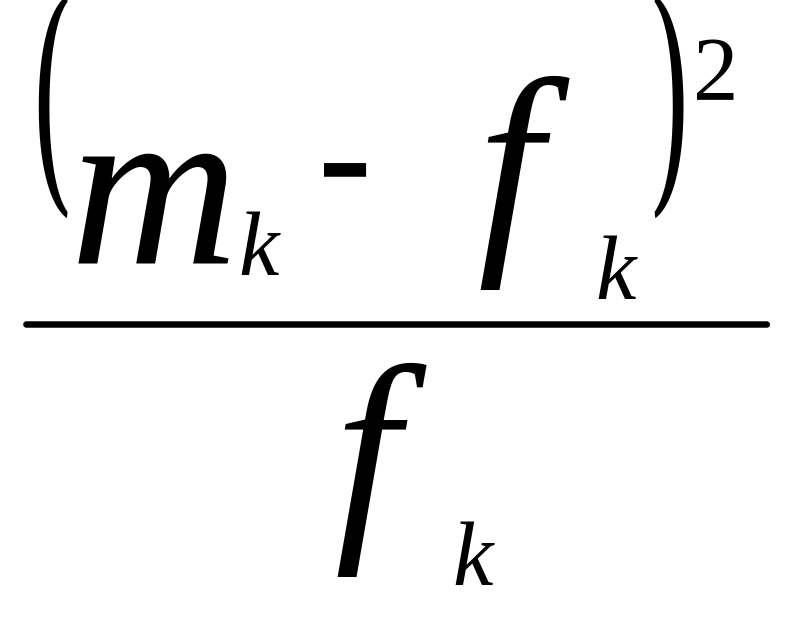
33	32.5		0.5	0.25	0.008
77	76.65		0.35	0.12	0.0016
95	94.9		0.1	0.01	0.0001
77	79.65		0.35	0.12	0.0016
47	47.45		-0.45	0.2	0.004
23	21.9		1.1	1.21	0.55
10	9.12		0.88	0.77	0.84
3	3.14		-0.14	0.02	0.006

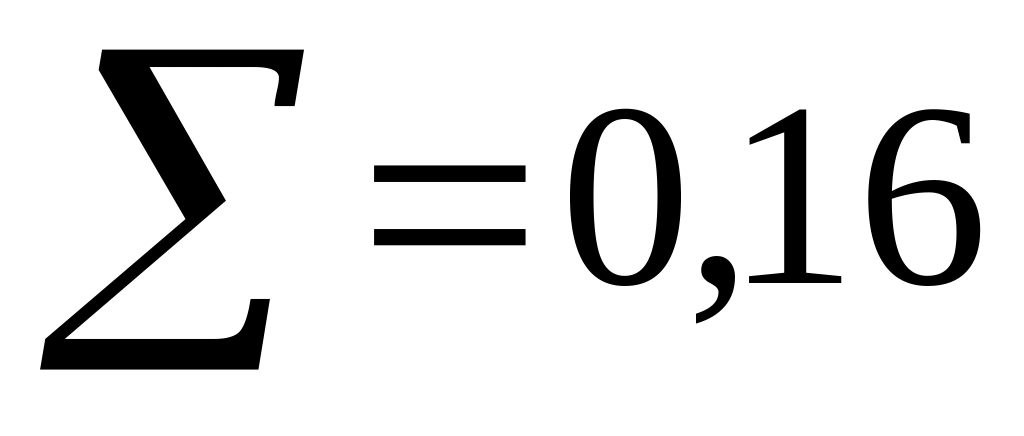
Сума даних останньої графи таблиці 4.8 і дає шукану величину Х². Отже, у приведеному випадку величина Х²=0.16. Кількість ступенів свободи К цього розподілу дорівнює кількості груп n мінус 2, тобто К=8-2=6. Підставимо значення Х² і числа ступенів свободи в (3.23) знайдемо величину критерію Романовського.

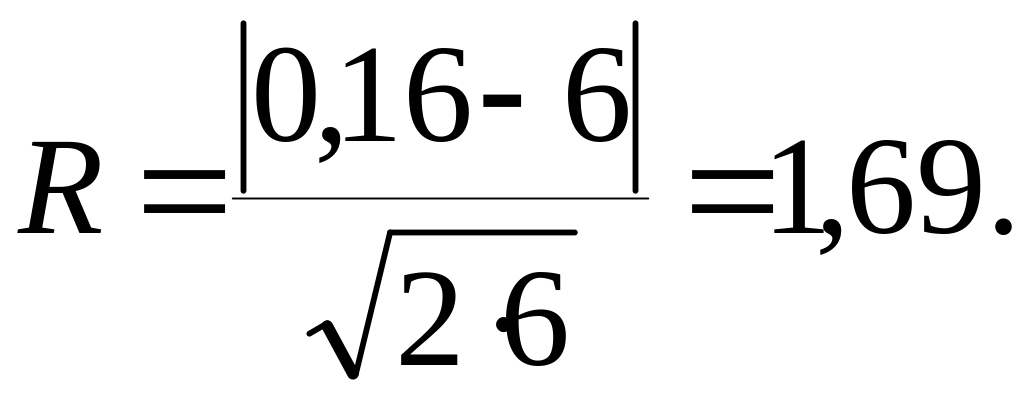
Тому що величина критерію романовского за своїм абсолютним значенням менше трьох, то для даного розподілу потоку викликів пожежних підрозділів модель закону розподілу Пуассона прийнятна для практичного використання.

Середній час обслуговування одного виклику визначається на основі даних інтервального варіаційного ряду (табл.3.3) за формулою

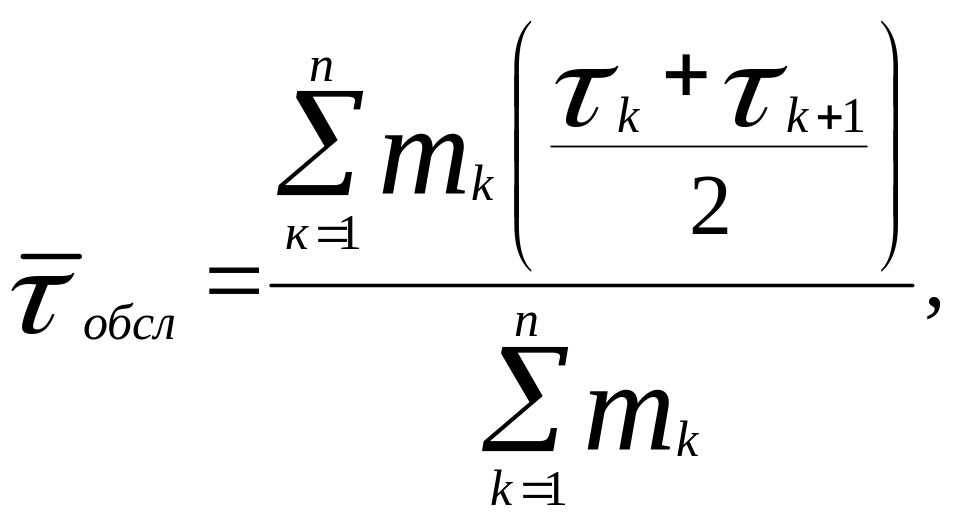(3.25)

де m_к -кількість викликів у тому або іншому інтервалі часу;

- нижня границя інтервалу;

- верхня границя інтервалу (вона ж є нижньою для наступного інтервалу);

n – кількість інтервалів.

Оскільки потік викликів пожежних підрозділів підкоряється законові Пуассона, то розподіл часу обслуговування повинен підкорятися показовому закону розподілу. Для опису емпіричного ряду за допомогою математичної моделі (експонентного закону розподілу) необхідно визначити теоретичну імовірність:

попадання величини в інтервал часу [ ; ]:

(3.26)

де 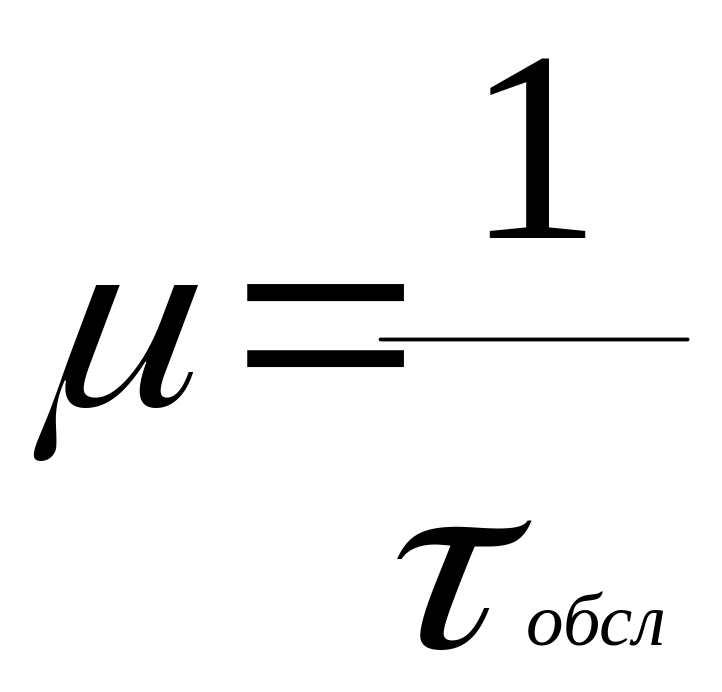- параметр експонентного закону розподілу.

Теоретичний розподіл кількості викликів за виділеними інтервалами значень часу обслуговування знаходиться по формулі:

(3.27)

де n – кількість інтервалів.

Перевірка відповідності емпіричного розподілу математичної моделі вираженої експоненціальним законом розподілу, здійснюється також за допомогою критерію Романовського.

Надано розподіл викликів пожежних підрозділів за часом обслуговування (таблиця 3.9). Потрібно графічно зобразити даний розподіл, визначити середній час обслуговування одного виклику, побудувати математичну модель розподілу часу обслуговування, перевірити ступінь відповідності емпіричного і теоретичного розподілів. Щоб побудувати гістограму розподілу викликів пожежних підрозділів за часом обслуговування (рис. 3.4), необхідно установити верхню границю останнього інтервалу таким чином, щоб величина інтервалу дорівнювала б величині інших інтервалів.

Таблиця 9.

Інтервал часу ,хв	0-15	15-30	30-45	45-60	60-75	75-90	90-105	105-120
Емпірична частота (число викликів)	220	173	150	110	90	80	51	8
Теоретична частота	275.8	191.7	134.4	90	61.3	42.7	29.5	19.98

Значення f_k проставляються в таблицю після проведення розрахунків.

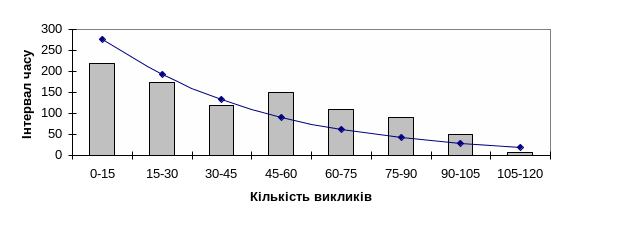Рис. 3.4. Розподілення викликів за часом обслуговування.

У нашому випадку =15 хвилин. Отже, верхня границя останнього інтервалу 75+15=90 хвилин. Середній час обслуговування складе:

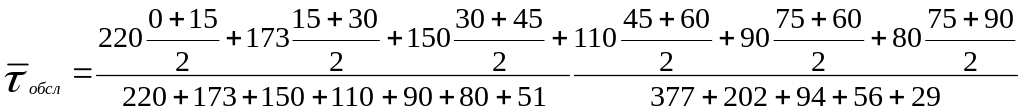
51*(75+90)/2+8*(105+120)/2=40.2 хвл

У цьому випадку 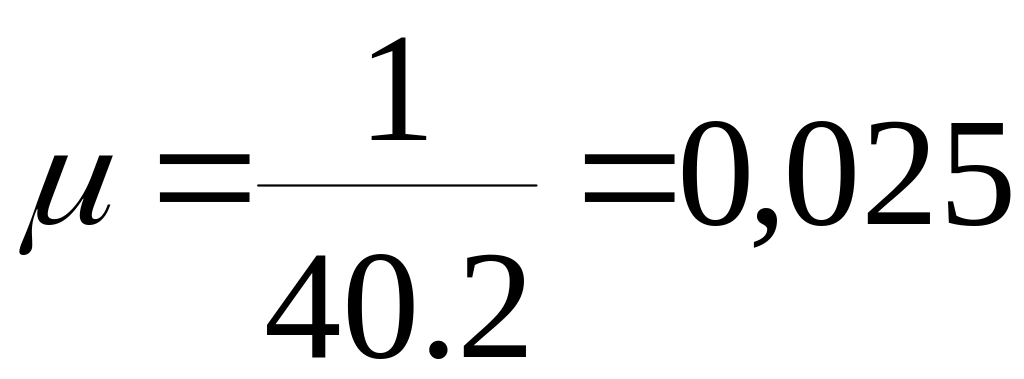хв^-1.

Знаходимо теоретичне значення імовірності Р_к={Р } попадання величини в інтервал часу за експоненціальним законом розподілу (3.26). Використовуючи вираження (3.27), знайдемо теоретичну кількість викликів f_k. Отримані дані заносимо в другий рядок таблиці 3,9 і на графік (малюнок 3.4). Визначення значення Х проведемо також як у попередньому прикладі, для чого складемо таблицю 3.10.

Таблиця 10

mk	fk	mk-fk	(mk-fk)2
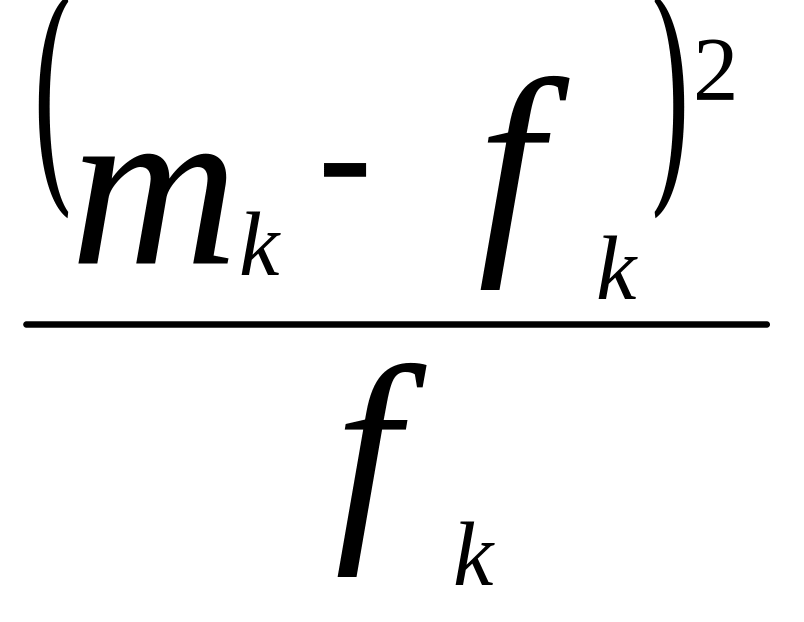
220	275,8	-55,8	3113,64	11,289
173	191,7	-18,7	349,69	1,82
150	134,4	15,6	243,36	1,81
110	90	20	400	1,44
90	61,9	28,1	789,6	12,7
80	42,7	37,3	1391,3	32,6
51	29,5	21,5	462,25	15,7
8	19,985	-11,985	143,6	7,18

X²=87,5

Таким чином Х²=87.5

Знайдемо кількість ступенів свободи даного розподілу k=8-2=6.

Підставимо значення X та кількість ступенів свободи в (3.23) знайдемо величину критерію Романовського:

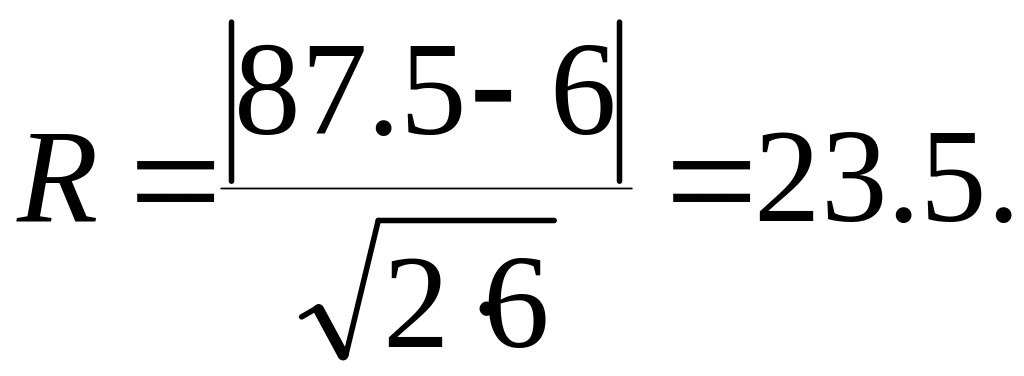
Так як величина критерію Романовського по своєму абсолютному значенню більше 3, то експонентний закон розподілу не можна прийняти як математичну модель даного емпіричного розподілу кількості викликів пожежних підрозділів за часом обслуговування.

Частість використання пожежних автомобілів визначається на підставі даних дискретного варіаційного ряду таблиця 3.3 гр.2 по формулі:

(3.28)

Дано (таблиця 4.11) розподіл виїздів по числу основних пожежних автомобілів, що виїжджали на них. Необхідно побудувати полігон розподілу виїздів по числу основних пожежних автомобілів, що виїжджали на них, і визначити частоту їхнього використання.

Таблиця 11

Число автомобілів, k	1	2	3	4	5	6	7	8	9
Число викликів, обслугованих автомобілем, mk	202	345	99	135	80	10	5	3	1
Частість використання автомобілів, ak	0,229	0,392	0,112	0,153	0,09	0,011	0,006	0,003	0,001

Будуємо полігон емпіричного розподілу (рисунок 3.5).

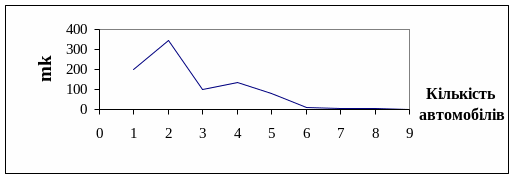
Рисунок 3.5. Розподіл кількості викликів за ознакою «кількість автомобілів».

По формулі (3.28) визначаємо емпіричну імовірність використання основних пожежних автомобілів щодо обслуговування викликів. Отримані результати заносимо до другого рядка таблиці 3.11.