Антивирусы для сайтов

• Серверный — устанавливается на веб-сервер. Поиск вирусов, в этом случае, происходит в файлах всего сервера.

• Скрипт или компонент CMS — выполняющие поиск вредоносного кода, непосредственно в файлах сайта.

• SaaS сервис — система централизованного управления, позволяющая управлять файлами, базами данных, настройками и компонентами веб-ресурсов на VDS и DS удаленно.

21. Формы представления информации. Преобразование непрерывных сообщений.

Текстовая, графическая, числовая, звуковая.

Преобразование непрерывных сообщений в цифровую форму в системах ИКМ, как отмечалось, сопровождается округлением мгновенных значений до ближайших разрешенных уровней квантования. Возникающая при этом погрешность представления является неустранимой, но контролируемой (так как не превышает половины шага квантования) (рис.2.2,г). Погрешность (ошибку) квантования, представляющую собой разность между исходным сообщением и сообщением, восстановленным по квантованным отсчетам, называют шумом квантования.

22. Дискретизация непрерывного сообщения. Теорема Котельникова. Преимущества дискретной формы.

 При передаче непрерывных сообщений по системам связи c использованием импульсной модуляции или кодирования возникает необходимость дискретизации сообщений по времени. В последнее время необходимость дискретизации непрерывных сигналов объясняется развитием методов квантования, дискретного анализа формы сигналов, развитием цифровой и вычислительной техники.

Сущность дискретизации заключается в том, что непрерывность во времени функции s(t) заменяется последовательностью коротких импульсов, амплитуды которых (координаты) ск в общем случае определяются с помощью

дискретных весовых функций x_к(t)   .

     Воспроизведение непрерывной функции по ее дискретным координатам производится с помощью системы базисных функций     Иногда весовые и базисные функции принимают одинаковыми    Ввиду сложности определения координатных функций более широкое распространение получили методы дискретизации, при которых сигнал s(t) заменяется совокупностью его мгновенных значений   , называемых выборками, или отсчетами. Роль весовых функций в этом случае играют d-функции   , Dt - шаг дискретизации (может быть неравномерным).   . Шаг дискретизации должен быть таким, чтобы было возможно восстановление непрерывной функции по ее отсчетам с допустимой точностью.

Равномерная дискретизация. Теорема Котельникова

     Правило выбора предельного шага при равномерной дискретизации с использованием модели сигнала с ограниченным спектром сформулировано академиком В. А. Котельниковым: «Любая непрерывная функция s(t), спектр которой ограничен частотой F_max полностью определяется последовательностью своих значений в моменты времени, отстоящие друг от друга на интервал  » Кроме того, теорема Котельникова дает и способ точного восстановления сигнала    по его отсчетам.

Доказательство

  причем    при           (1)

Разложим функцию    в частотной области на конечном интервале    (с периодом   ) в комплексный ряд Фурье :

 где                                                                (2)

                                                       (3)

Сравнивая интегралы в (3) и (1), видно, что они равны при   , т. е.   тогда

                                                                             (4)

Подставляем (4) в (2), а затем в (1)

  

т. к. суммирование по от -¥ до +¥, то можно заменить знак у .

                                  (5)

Максимальные значения членов ряда будут при    и равны   , при этом все остальные члены ряда равны нулю, т. е. при     функция s(t) точно передается рядом. Во все другие моменты времени необходимо суммировать бесконечное число отсчетов, чтобы передать s(t) точно.

     Представление сигнала в виде ряда Котельникова (5) является частным случаем разложения   . Роль коэффициента    выполняют отсчеты   Базисными являются функции вида    Они называютсяфункциями отсчетов. Функции отсчетов ортогональны, т. к.

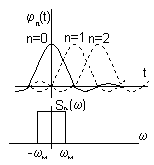
Спектральная плотность функции отсчета на частотной шкале есть прямоугольник шириной    (идеальный фильтр н.ч.).      Теорема Котельникова распространяется на непрерывный стационарный случайный процесс с ограниченным спектром

Такой процесс представляется (заменяется) суммой квазидетерминированных процессов, где роль ортогональных детерминированных функций выполняют функции отсчета, а случайных коэффициентов - величины выборок:

 , где 

Т. о., при указанных ограничениях случайный процесс полностью определяется счетным множеством случайных величин - координат процесса.

     Практическое осуществление дискретизации сигнала    рядом Котельникова и дальнейшее его восстановление сводится к следующему. На передающей стороне через интервалы    определяются мгновенные значения    сигнала и передаются в канал связи в виде d-импульсов с площадью, равной отсчету    На приемной стороне такая последовательность импульсов пропускается через идеальный фильтр нижних частот    При длительной передаче сигнал на выходе фильтра будет точно воспроизводить переданный непрерывный сигнал

     Искажения восстановленного (по Котельникову) сигнала могут происходить по следующим причинам. Реальный сигнал имеет конечную длительность и, следовательно, обладает неограниченным спектром. Дискретизация его с интервалом   ограничивает спектр    и, следовательно, искажает воспроизведение сигнала. С другой стороны, и при передаче непрерывного сигнала вследствие ограничения полосы пропускания аппаратуры сигнал искажается. Однако при дискретизации появляется дополнительное искажение за счет конечности числа отсчетов за ограниченное время длительности сигнала, в то время как их должно быть бесконечно много, т. к. ограничению спектра сигнала соответствует увеличение его длительности до бесконечности. Такое двойное искажение хотя и может частично компенсироваться, но создает трудности для теоретического анализа погрешности передачи.

     Несмотря на невозможность точного воспроизведения сигнала ограниченной длительности (чем более короткий сигнал, тем больше ошибка воспроизведения), дискретизация и восстановление по Котельникову используется весьма широко при преобразовании сигнала в цифровую форму.

Сигнал — материальный носитель информации, используемый для передачи сообщений в системе связи. Сигнал может генерироваться, но его приём не обязателен, в отличие отсообщения, которое должно быть принято принимающей стороной, иначе оно не является сообщением. Сигналом может быть любой физический процесс, параметры которого изменяются в соответствии с передаваемым сообщением.

Различные параметры физических процессов с помощью датчиков обычно преобразуются в электрические сигналы. Как правило, ими являются непрерывно изменяющиеся ток или напряжение, но возможно поступление и импульсных сигналов, как, например. в радиолокации.

Печатный текст отображается буквами, цифрами и другими знаками.

Хотя поступающую информацию можно хранить, передавать и

обрабатывать как в виде непрерывных, так и в виде дискретных сигналов, на современном этапе развития информационной техники предпочтение

отдается дискретным сигналам, поэтому сигналы, как правило,

преобразуются в дискретные. С этой целью каждый непрерывный сигнал

подвергается операциям квантования по времени (дискретизации) и по

уровню.

Понятие Дискретность - (от лат discretus — разделённый, прерывистый)— свойство, противопоставляемое , непрерывностти. Дискретность - всеобщее свойство материи. Под дискретностью понимают:

1. Нечто, изменяющееся между несколькими различными стабильными состояниями подобно выключателю, который может быть либо включён, либо выключен.

2. Нечто, состоящее из отдельных частей, прерывистость, дробность. Например, дискретный спектр, дискретные структуры, дискретные сообщения.

Дискретизация- это преобразование непрерывных изображений и звука в набор дискретных значений в форме кодов.