1. Предел функции на бесконечности и в точке. В точке: Число А называется пределом функции в точке х_о (или при х→х_о), если для любого положительного ε найдется такое положительное число δ, что для все х¹х_о, удовлетворяющих неравенству |х-х_о|<δ, выполняется неравенство |ƒ(х)-А|<ε.

Геометрический смысл предела функции:

если для любой ε-окрестности точки А найдется такая δ-окрестность точки х_о, что для всех х¹хо из етой  δ-окрестность соответствующие значения функции ƒ(х) лежат в ε-окрестности точки А. Иными словами, точки графика функции у=ƒ(х) лежат внутри полосы шириной 2ε, ограниченной прямыми у=А+ ε , у=А-ε (см. рис. 110). Очевидно, что величина δ зависит от выбора ε, поэтому пишут δ=δ(ε).

На бесконечности(Коши): Пусть числовая функция   задана на множестве  , в котором отыщется сколь угодно большой элемент, то есть для всякого положительного   в нём найдётся элемент, лежащий за границами отрезка  . В этом случае число  называется пределом функции   на бесконечности, если для произвольного положительного числа   отыщется отвечающее ему положительное число   такое, что для всех точек, превышающих   по абсолютному значению, справедливонеравенство  .

-Пусть числовая функция   задана на множестве  , в котором для любого числа   найдётся элемент, лежащий правее него. В этом случае число   называется пределом функции   на плюс бесконечности, если для произвольного положительного числа   отыщется отвечающее ему положительное число   такое, что для всех точек, лежащих правее  , справедливо неравенство  .

-Пусть числовая функция   задана на множестве  , в котором для любого числа   найдётся элемент, лежащий левее него. В этом случае число   называется пределом функции   на минус бесконечности, если для произвольного положительного числа   отыщется отвечающее ему положительное число   такое, что для всех точек, лежащих левее  , справедливо неравенство  .

2. Свойства пределов функций.

-Предел суммы/разности двух функций равен сумме/разности их пределов:

-Предел произведения двух функций равен произведению их пределов:

-Предел частного двух функций равен частному их пределов, при условии, что предел знаменателя не равен нулю:

-Константу можно выносить за знак предела:

 -Предел степени с натуральным показателем равен степени предела:

Бесконечно малые и беск. большие величины, их свойства. Бесконечно малая — числовая функция или последовательность, которая стремится к нулю. Бесконечно большая — числовая функция или последовательность, которая стремится к бесконечности определённого знака. Свойства бесконечно малых:

-Алгебраическая сумма конечного числа бесконечно малых функций есть бесконечно малая функция. -Произведение бесконечно малых — бесконечно малая. -Произведение бесконечно малой последовательности на ограниченную — бесконечно малая. Как следствие, произведение бесконечно малой на константу — бесконечно малая. -Если   — бесконечно малая последовательность, сохраняющая знак, то   — бесконечно большая последовательность.

 Свойства б.б. функций: -Сумма двух б.б. одного знака при   является б.б. при   . -Сумма б.б. функции при   и ограниченной в окрестности точки а функции является б.б. при  . Первый «замечательный предел» и его следствия. Предел отношения синуса к его аргументу равен единице в случае, когда аргумент стремится к нулю. Следствия:

Доказательство следствий

Второй замечательный предел и его следствия. Число   часто называют основанием натуральных логарифмов.  

Следствия:

Доказательство следствия:

Неопределенности и их раскрытие. Теорема Лопиталя.  (Правило Лопиталя раскрытия неопределенностей вида  ).

Пусть функции y = f(x), y = g(x) непрерывны и дифференцируемы в некоторой окрестности числа a (a может равняться ∞), за исключением, быть может, числа a ; при этом g, g' не равны нулю в этой окрестности.

Кроме этого, пусть  .

Тогда, если 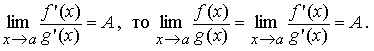  (Правило Лопиталя раскрытия неопределенностей вида  ).

Пусть функции y = f(x), y = g(x) непрерывны и дифференцируемы в некоторой окрестности числа a (a может равняться ∞), за исключением a.

Кроме этого, пусть  .

Тогда, если 

Производная функции одной переменной. Эконом. смысл производной. Производная функции   в точке   определяется как предел отношения приращения функции к приращению аргумента при стремлении приращения аргумента к нулю:

где 

Графически это тангенс угла наклона касательной к кривой, изображающей функцию  .

При достаточно малых изменениях   аргумента выполнено равенство

В общем случае именно такая форма определения принимается за основу для обобщения понятия производной. Односторонние производные Определяются также односторонние производные, где вместо соответствующего предела используется односторонний (левосторонний и правосторонний) предел. Правосторо́нняя произво́дная  обозначается символами   Левосторо́нняя произво́дная  обозначается символами  . Обычная производная существует тогда и только тогда, когда существуют равные между собой односторонние производные (их величина и равна производной). Производные высших порядков Поскольку производная функции одной переменной также является некоторой функцией одной переменной, то можно рассматривать производную производной -вторую производную и вообще производную любого порядка   (некоторое натуральное число) - Применение дифференциального исчисления к исследованию экономических объектов и процессов на основе анализа этих предельных величин получило название предельного анализа. Предельные величины характеризуют не состояние (как суммарная или средняя величины), а процесс изменения экономического объекта. Таким образом, производная выступает как скорость изменения некоторого экономического объекта (процесса) по времени или относительно другого исследуемого фактора. Производная функции показывает, как изменяется её значение при малом изменении аргумента.

Производная суммы, произведения и частного 2 ф-ий. - Производная суммы (разности) двух функций равна сумме (разности) производных этих функций: (u±ν)'=u'±ν'.  -Производная произведения двух функций равна произведению производной первого сомножителя на второй плюс произведение первого сомножителя на производную второго: (u•ν)'=u'ν+v'u. -Производная частного двух функций     если ν(х)≠0 равна дроби, числитель которой есть разность произведений знаменателя дроби на производную числителя и числителя дроби на производную знаменателя, а знаменатель есть квадрат прежнего знаменателя:

Производная сложной функции. Рассмотрим сложную функцию y = y(u(x)) Если функции y = y(u), u = u(x) дифференцируемы (т.е. существуют производные y'_u, u'_x), тогда сложная функция y = y(u(x)) дифференцируема и y'_x = y'_u u'_x. Доказательство: Если аргумент x получит приращение Δx, то функция u получит приращение Δu = u(x + Δx) − u(x), а функция y получит приращение Δy = y(u + Δu) − y(u). Но тогда, воспользовавшись свойствами предела функции, получаем

Производная обратной функции Рассмотрим функцию y = f(x), для которой существует обратная функция x = g(y). Если обратная функция x = g(y) дифференцируема и g'(y) ≠ 0, то функцияy=f(x) дифференцируема, и  Доказательство: Если аргумент x получит приращение Δx, то функция f получит приращение Δy = f(x + Δx) − f(x). С другой стороны, для обратной функции g приращения Δx, Δy связаны следующим образом:Δx=g(y + Δy) − g(y). Тогда получаем

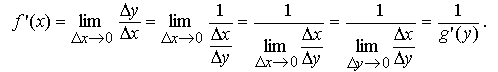
 Неявно заданная функция Если функция задана уравнением у=ƒ(х), разрешенным относительно у, то функция задана в явном виде (явная функция). Под неявным заданием функции понимают задание функции в виде уравнения F(x;y)=0, не разрешенного относительно у. Всякую явно заданную функцию у=ƒ (х) можно записать как неявно заданную уравнением ƒ(х)-у=0, но не наоборот. Не всегда легко, а иногда и невозможно разрешить уравнение относительно у (например, у+2х+cosy-1=0 или 2^у-х+у=0). Если неявная функция задана уравнением F(x; у)=0, то для нахождения производной от у по х нет необходимости разрешать уравнение относительно у: достаточно продифференцировать это уравнение по x, рассматривая при этом у как функцию х, и полученное затем уравнение разрешить относительно у'. Производная неявной функции выражается через аргумент х и функцию у. Функция, заданная параметрически Пусть зависимость между аргументом х и функцией у задана параметрически в виде двух уравнений

где t — вспомогательная переменная, называемая параметром. Найдем производную у'_х, считая, что функции (21.1) имеют производные и что функция х=x(t) имеет обратную t=φ(х). По правилу дифференцирования обратной функции

Функцию у=ƒ(х), определяемую параметрическими уравнениями (21.1), можно рассматривать как сложную функцию у=y(t), где t=φ(х). По правилу дифференцирования сложной функции имеем: у'_х=y'_t•t'_x. С учетом равенства (21.2) получаем

Полученная формула позволяет находить производную у'_х от функции заданной параметрически, не находя непосредственной зависимости у от х.

Производная показательно степенной функции Рассмотрим показательно степенную функцию y = u(x)^v(x) Пусть функции u = u(x), v = v(x) дифференцируемы, тогда функция y = u(x)^v(x) дифференцируема и

Доказательство Так как ln y = v(x) ln u(x), то, продифференцировав это равенство, получаем

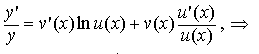
Производная показательной функции

Пример дифференцирования показательной функции Найти производную функции  y = 3^5x Решение Выразим основание показательной функции через число e.  3 = e^{ln 3}  Тогда    Вводим переменную  z = 5ln 3 · x.  Тогда    По таблице производных:    Поскольку 5ln 3 - это постоянная, то производная z по x равна:    По правилу дифференцирования сложной функции: 

Производная логарифмической функции 

Доказательство Вначале докажем теорему для функции y = ln x. Если аргумент x получит приращение Δx, то функция y = ln x получит приращение  Воспользовавшись вторым замечательным пределом, свойствами предела функции и свойствами логарифмической функции, получаем

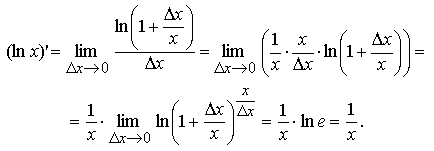
Теперь, так как   то, вынося постоянную за знак производной, получаем

Производные тригонометрических функций 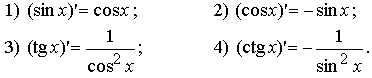Доказательство Если аргумент x получит приращение Δx, то функция y = sin x получит приращение

Воспользовавшись первым замечательным пределом и свойствами предела функции, получаем

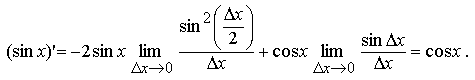Утверждение 1) доказано. Утверждение 2) доказывается аналогично, заметим только, что приращение функции y = cos x можно записать так:

Производные обр. тригонометр. Функций. Доказательство Если y = arcsin x, то x = sin y. Получаем  . Тогда   и утверждение 1) доказано. Остальные утверждения теоремы доказываются аналогично.

 Производные высоких порядков Рассмотрим дифференцируемую функцию y = f (x). Как было отмечено в п.1.1, ее производная f' сама является функцией. Может оказаться, что функция f' также является дифференцируемой. Дифференцируя f', мы получим еще одну функцию, которую называют второй производной от функции f и обозначают так:

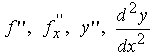Рассуждая аналогичным образом, можно определить производную любого порядка: третьего, четвертого и т.д. Производные третьего порядка обозначают следующим образом:

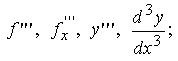а производные n–го порядка так:

Если функция y = f (x) имеет производные второго, третьего, n–го порядков, то такую функцию называют соответственно дважды дифференцируемой, трижды дифференцируемой, nраз дифференцируемой.

Дифференциал. Произведение f ' (x) Δx называют дифференциалом функции y = f(x) и обозначают dy или df(x), т.е. dy = f'(x)Δx. Дифференциал суммы, произведения, частного  Пусть функции u = u(x), v = v(x) дифференцируемы. Тогда

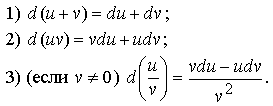 Дифференциалы высоких порядков. Рассмотрим n раз дифференцируемую функцию y=f(x). Ее дифференциал dy = f '(x)dxявляется функцией от x, причем от x зависит только f '(x) , а dx является приращением аргументаΔx и от x не зависит. Так как dy является функцией от x, то можно говорить о дифференциале этой функции:   Дифференциал дифференциала d(dy) называется вторым дифференциалом функцииy=f(x) и обозначается так: d²y. Аналогично определяются дифференциалы более высокого порядка:

Рассмотрим сложную функцию y = f(u(x)). Пусть функции y = f(u), u = u(x) дважды дифференцируемы. Выразим второй дифференциал d²y сложной функции y = f(u(x)) через u, du:

Таким образом, дифференциалы высоких порядков не обладают свойством инвариантности формы.

 Первообразная и неопределенный интеграл Первообразной функцией для функции f(x) называется такая функция F(х), производная которой равна данной функции

F'(x) = f(x). Обозначение

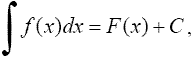
где F'(x) = f(x). Функция f(x) называется подынтегральной функцией, а выражение f(x)dx - подынтегральным выражением. Свойства неопределенного интеграла

1°. Производная неопределенного интеграла равна подынтегральной функции; дифференциал от неопределенного интеграла равен подынтегральному выражению, т.е.

2°. Неопределенный интеграл от дифференциала некоторой функции равен сумме этой функции и произвольной постоянной, т.е.

3°. Постоянный множитель можно вынести из под знака интеграла, т.е. если k = const ≠ 0, то

4° . Неопределенный интеграл от алгебраической суммы двух функций равен алгебраической сумме интегралов от этих функций в отдельности.

Интегрирование элементарных функций. Интеграл элементарной функции не всегда сам является элементарной функцией. Наиболеераспространенные функции, интегралы которых найдены, собраны в таблице интегралов. В общем случаеимеет место теорема:

Теорема Лиувилля. Если интеграл от элементарной функции   сам являетсяэлементарной функцией, то он представим в виде

где A_i — некоторые комплексные числа, а ψ_i — алгебраические функции своих аргументов. Метод замены переменной (метод подстановки) Метод интегрирования подстановкой заключается во введении новой переменной интегрирования (то есть подстановки). При этом заданный интеграл приводится к новому интегралу, который является табличным или к нему сводящимся. Общих методов подбора подстановок не существует. Умение правильно определить подстановку приобретается практикой. Пусть требуется вычислить интеграл   Сделаем подстановку   где   — функция, имеющая непрерывную производную. Тогда   и на основании свойства инвариантности формулы интегрирования неопределенного интеграла получаем формулу интегрирования подстановкой:

Интегрирование по частям .  — применение следующей формулы для интегрирования:

Или:

В частности, с помощью n-кратного применения этой формулы находится интеграл

где   — многочлен  -й степени.

Интегрирование дробно-рациональных выражений. Неопределенный интеграл от любой рациональной дроби на всяком промежутке, на котором знаменатель дроби не обращается в ноль, существует и выражается через элементарные функции, а именно он является алгебраической суммой суперпозиции рациональных дробей, арктангенсов и рациональных логарифмов.

Сам метод заключается в разложении рациональной дроби на сумму простейших дробей.

Всякую правильную рациональную дробь  , знаменатель которой разложен на множители

можно представить (и притом единственным образом) в виде следующей суммы простейших дробей:

где   — некоторые действительные коэффициенты, обычно вычисляемые с помощью метода неопределённых коэффициентов.

Интегрирование тригонометрических функций 1°. Интегралы вида

находятся с помощью тригонометрических формул

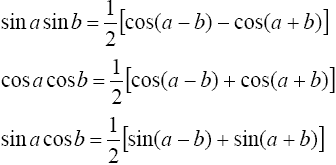2°. Интегралы вида

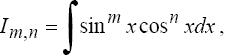где m и n - четные числа находятся с помощью формул понижения степени

Если хотя бы одно из чисел m или n - нечетное, то полагают (пусть m = 2k + 1)

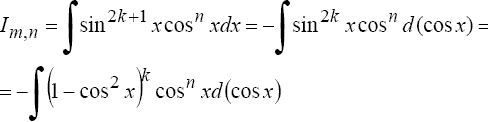
Универсальной тригонометрической подстановкой называется подстановка вида 

В англоязычной литературе в честь выдающегося немецкого математика Карла Вейерштрасса (1815 - 1897) называется подстановкой Вейерштрасса.

Указанная подстановка применяется при интегрировании, когда подынтегральное выражение рационально зависит от тригонометрических функций. Указанная замена позволяет свести интеграл от тригонометрической функции к интегралу от рациональной функции.

При этом следует учесть, что из равенства   получаем:

26.Определенный интеграл. Формула Ньютона – Лейбница.

Понятие определённого интеграла

Определённым интегралом от непрерывной функции f(x) на конечном отрезке [a, b] (где  ) называется приращение какой-нибудь её первообразной на этом отрезке. (Вообще, понимание заметно облегчится, если повторить тему неопределённого интеграла) При этом употребляется запись

Числа a и b называются соответственно нижним и верхним пределами интегрирования, а отрезок [a, b] – отрезком интегрирования.

Таким образом, если F(x) – какая-нибудь первообразная функция для f(x), то, согласно определению,

            (38)

При a = b по определению принимается

Равенство (38) называется формулой Ньютона-Лейбница. Разность F(b) – F(a) кратко записывают так:

Поэтому формулу Ньютона-Лейбница будем записывать и так:

                   (39)

Докажем, что определённый интеграл не зависит от того, какая первообразная подынтегральной функции взята при его вычислении. Пусть F(x) и Ф(х) – произвольные первообразные подынтегральной функции. Так как это первообразные одной и той же функции, то они отличаются на постоянное слагаемое: Ф(х) = F(x) + C. Поэтому

Тем самым установлено, что на отрезке [a, b] приращения всех первообразных функции f(x) совпадают.

Таким образом, для вычисления определённого интеграла необходимо найти любую первообразную подынтегральной функции, т.е. сначала следует найти неопределённый интеграл. Постоянная С из последующих вычислений исключается. Затем применяется формула Ньютона-Лейбница: в первообразную функцию подставляется значение верхнего предела b, далее - значение нижнего предела a и вычисляется разностьF(b) - F(a). Полученное число и будет определённым интегралом.

27. Метод интегрирования по частям определенного интеграла.

Интегрирование по частям

Если функции u = u(х) и v = v(x) имеют непрерывные производные на отрезке [а; b], то имеет место формула

▼На отрезке [а; b] имеет место равенство (uv)' = u'v+uv'. Следовательно, функция uv есть первообразная для непрерывной функции u'v+uv'. Тогда по формуле Ньютона-Лейбница имеем:

Следовательно,

▲

Формула (39.2) называется формулой интегрирования по частям для определенного интеграла.

 

28. Вычисление площадей. Объемов и длин кривых с помощью определенного интегрирования.

1.Площадь фигуры, ограниченной графиком непрерывной отрицательной на промежутке [ a ; b ] функции f (x), осью Ох и прямыми х=а и х= b :

2.Площадь фигуры, ограниченной графиками непрерывных функций f (x),   и прямыми х=а, х= b :

3.Площадь фигуры, ограниченной графиками непрерывных функций f (x) и  :

4.Площадь фигуры, ограниченной графиками непрерывных функций f (x),   и осью Ох:

Длина дуги явно заданной кривой Если плоская кривая задана явно уравнением y= y x , x Э a b; , где y x – непрерывно дифференцируемая на a b; функция, то ее длина равна

Пусть функция y= y x непрерывна и неотрицательна на отрезке a b; . Объ- ем V тела, образованного вращением вокруг оси Ox фигуры, огра- ниченной графиком функции y= y x , отрезками прямых x= a и x= b и отрез- ком оси Ox , равен

29. Дифференцирование функции нескольких переменных.

Частной производной по   от функции   называется предел отношения частного приращения этой функции   по   к приращению  , когда последнее стремится к нулю:  .

Частной производной по   от функции   называется предел отношения частного приращения этой функции   по   к приращению  , когда последнее стремится к нулю:  .

Пусть задана функция   . Если аргументу   сообщить приращение  , а аргументу   – приращение  , то функция  получит приращение  , которое называется полным приращением функции и определяется формулой:  .

Функция  , полное приращение   которой в данной точке может быть представлено в виде суммы двух слагаемых (выражения, линейного относительно   и  , и величины бесконечно малой высшего порядка относительно  ):  , где   и   стремятся к нулю, когда   и   стремятся к нулю (т.е. когда  ), называется дифференцируемой в данной точке.

Линейная (относительно   и  ) часть полного приращения функции называется полным дифференциалом и обозначается  :  , где   и   – дифференциалы независимых переменных, которые, по определению, равны соответствующим приращениям   и  .

Частные производные от частных производных первого порядка называются частными производными второго порядка. Для функции двух переменных   их четыре:

30. Интегрирование функций нескольких переменных

• Определение. Если каждой паре действительных чисел (x; y) из области D по определенному правилу ставится в соответствие только одно число z из области Е, то говорит, что на множестве D задана функция двух переменных z = z(x, y).

Значение z(a; b) функции z = z (x, y) есть значение этой функции, вычисленное при x = a, y = b.

31. Диф. уравнения определение , понятие решения диф уравнения.

 

Определение 1. Уравнение, содержащее независимую переменную, функцию от этой независимой переменной и ее производные различных порядков, называется дифференциальным уравнением.

Определение 2. Наивысший порядок производной, входящей в дифференциальное уравнение, называется порядком дифференциального уравнения.

Дифференциальное уравнение  n-го порядка имеет вид

F(x,y,y',y'', …, y⁽ⁿ⁾)=0.

Определение 3. Дифференциальное уравнение n-го порядка называется линейным, если неизвестная функция и все ее производные входят в него в первой степени. Общий вид линейного дифференциального уравнения   n-го порядка:

a₀(x)y⁽ⁿ⁾ + a₁(x)y^(n-1) + ... + a_n-1(x)y⁽¹⁾ + a_n(x)y = f(x).                                         (1)

Определение 4. Линейное дифференциальное уравнение (1) называется однородным, если  f(x)  0, и неоднородным - в противном случае.

Примеры дифференциальных уравнений:

y'' - sin x y' + (cos x) y = tg x          - линейное,

sin y' - cos y = ctg x                         - нелинейное,

y''' - y' = 0                                         - линейное,

(y^IV)² - 3y''' + y = 1                          - нелинейное.

Определение 5. Решением дифференциального уравнения называется любая функция y = (x), при подстановке которой в уравнение будет получено тождество. Процесс нахождения решения дифференциального уравнения называется интегрированием дифференциального уравнения, график решения называют интегральной кривой.

Пример 1.     y' - f(x) = 0 ,                          Пример 2.     y'' = 0,

y' = f(x),                                                        y' = C,

y =  f(x)dx + C.                                          y = C₁x + C₂.

Определение 6. Решение дифференциального уравнения n-го порядка, содержащее n произвольных постоянных, называется общим решением дифференциального уравнения.

Определение 7. Если в результате интегрирования дифференциального уравнения получена зависимость между y и x, из которой не удается явно выразить y через x (т.е. неизвестная функция задана неявно), то данную зависимость называют общим интегралом дифференциального уравнения.

Определение 8. Решение, полученное из общего при конкретных значениях произвольных постоянных, называется частным решением.

Пример. y'' + y = 0.

y = C₁ cos x + C₂ sin x - общее решение.

у₁ = 3 cos x -2 sin x - частное решение.

32.Задача Коши. Геометрический смысл диф уравнения первого порядка.

Задача Коши (задача с начальным условием). Пусть функция f(x, y) определена в области D, точка  . Требуется найти решение уравнения

;

(8)

удовлетворяющее начальному условию

y(x0) = y0;

(9)

(начальное условие (9) часто записывают в форме  ).  Теорема Коши (существования и решения задачи Коши). Если в области D функция f(x, y) непрерывна и имеет непрерывную частную производную  , то для любой точки   в окрестности точки x₀ существует единственное решение задачи ((8),(9)).

  . Геометрический смысл диф уравнения первого порядка

Общий вид дифференциального уравнения первого порядка: F (x, y, y ' ) = 0.

Если его возможно разрешить относительно производной y ', то оно приводится к виду y ' = f (x, y).       (3.1)

Такая форма дифференциального уравнения первого порядка называется нормальной, а уравнение является разрешимым относительно производной от искомой функции.

   Выясним геометрический смысл дифференциального уравнения первого порядка вида (3.1).

   Общее решение геометрически задает однопараметрическое семейство интегральных кривых.

   Решение y = y (x) уравнения (3.1) представляет собой на плоскости XOY кривую, а y ' — угловой коэффициент касательной к этой кривой в точке M(x, y). Уравнение (3.1) дает, таким образом, соотношение между координатами точки и угловым коэффициентом касательной к интегральной кривой в этой точке.

   Задание уравнения (3.1) означает, что в каждой точке M (x, y) области, где определена функция f (x, y), задано направление касательной к интегральной кривой в точке M (x, y). Значит, имея уравнение (3.1) мы получаем поле направлений. Это поле графически можно изобразить, поместив в каждой точке M (x, y) черточку, наклоненную к оси Ox под углом, тангенс которого равен f (x, y).

   Задача интегрирования уравнения (3.1) заключается в том, чтобы найти семейство кривых, у которых касательная к каждой точке совпадает с направлением поля в этих точках. Такое истолкование уравнения (3.1) дает графический способ построения его решения.

33. Диф уравнения с разделяющимися переменными.

Дифференциальное уравнение первого порядка y' = f(x,y) называется уравнением с разделяющимися переменными, если функцию f(x,y) можно представить в виде произведения двух функций, зависящих только от x и y:

где p(x) и h(y) − непрерывные функции.  Рассматривая производную y' как отношение дифференциалов  , перенесем dx в правую часть и разделим уравнение на h(y):

Разумеется, нужно убедиться, что h(y) ≠ 0. Если найдется число x₀, при котором h(x₀) = 0, то это число будет также являться решением дифференциального уравнения. Деление на h(y) приводит к потере указанного решения.  Обозначив  , запишем уравнение в форме:

Теперь переменные разделены и мы можем проинтегрировать дифференциальное уравнение:

где C − постоянная интегрирования.  Вычисляя интегралы, получаем выражение

описывающее общее решение уравнения с разделяющимися переменными.

34. Уравнение в полных дифференциалах.

Определение уравнения в полных дифференциалах

Дифференциальное уравнение вида

называется уравнением в полных дифференциалах, если существует такая функция двух переменных u(x,y) с непрерывными частными производными, что справедливо выражение

Общее решение уравнения в полных дифференциалах определяется формулой

где C − произвольная постоянная.

Необходимое и достаточное условие

Пусть функции P(x,y) и Q(x,y) имеют непрерывные частные производные в некоторой области D. Дифференциальное уравнение P(x,y)dx + Q(x,y)dy = 0 будет являться уравнением в полных дифференциалах тогда и только тогда, если справедливо равенство:

Алгоритм решения уравнения в полных дифференциалах

1. Сначала убедимся, что дифференциальное уравнение является уравнением в полных дифференциалах, используя необходимое и достаточное условие:

           

2. Затем запишем систему двух дифференциальных уравнений, которые определяют функцию u(x,y):

           

3. Интегрируем первое уравнение по переменной x. Вместо постоянной C запишем неизвестную функцию, зависящую от y:

           

4. Дифференцируя по переменной y, подставим функцию u(x,y) во второе уравнение:

           

Отсюда получаем выражение для производной неизвестной функции φ(y):

           

5. Интегрируя последнее выражение, находим функцию φ(y) и, следовательно, функцию u(x,y):

           

6. Общее решение уравнения в полных дифференциалах записывается в виде:

        

 

  35. Линейные диф уравнения первого порядка .

Определение линейного уравнения первого порядка

Дифференциальное уравнение вида

где a(x) и b(x) − непрерывные функции x, называтся линейным неоднородным дифференциальным уравнением первого порядка. Мы рассмотрим два метода решения указанных уравнений:

• Использование интегрирующего множителя;

• Метод вариации постоянной.

Использование интегрирующего множителя

Если линейное дифференциальное уравнение записано в стандартной форме:

то интегрирующий множитель определяется формулой:

Умножение левой части уравнения на интегрирующий множитель u(x) преобразует ее в производную произведения y(x)u(x).  Общее решение диффференциального уравнения выражается в виде:

где C − произвольная постоянная

36. Диф уравнения Бернулли

Дифференциальное уравнение Бернулли имеет вид  . При n = 1 это дифференциальное уравнение становится уравнением с разделяющимися переменными  .

Одним из методов решения дифференциального уравнения Бернулли является сведение его клинейному неоднородному дифференциальному уравнению первого порядка введением новой переменной  . Действительно, при такой замене имеем   и дифференциальное уравнение Бернулли примет вид

Так дифференциальное уравнение Бернулли приводится к линейному неоднородному дифференциальному уравнению первого порядка. После решения этого уравнения и проведения обратной замены получаем искомое решение.

37. Однородные диф уравнения первого порядка.

Определение однородного дифференциального уравнения

Дифференциальное уравнение первого порядка

называется однородным, если правая часть удовлетворяет соотношению

для всех значений t. Другими словами, правая часть должна являться однородной функцией нулевого порядка по отношению к переменным x и y:

Однородное дифференциальное уравнение можно также записать в виде

или через дифференциалы:

где P(x,y) и Q(x,y) − однородные функции одинакового порядка.

Определение однородной функции

Функция P(x,y) называется однородной функцией порядка n, если для всех t > 0 справедливо следующее соотношение:

Решение однородных дифференциальных уравнений

Однородное дифференциальное уравнение можно решить с помощью подстановки y = ux, которая преобразует однородное уравнение в уравнение с разделяющимися переменными.  Дифференциальное уравнение вида

преобразуется в уравнение с разделяющимися переменными посредством переноса начала системы координат в точку пересечения прямых линий, заданных в уравнении. Если указанные прямые параллельны, то дифференциальное уравнение сводится к уравнению с разделяющимися переменными путем замены переменной:

38. Линейные однородные диф уравнения второго порядка с постоянными коэффициентами.

Рассмотрим линейное дифференциальное уравнение вида

где p, q − постоянные коэффициенты.  Для каждого такого дифференциального уравнения можно записать так называемое характеристическое уравнение:

Обшее решение однородного дифференциального уравнения зависит от корней характеристического уравнения, которое в данном случае будет являться квадратным уравнением. Возможны следующие случаи:

1. Дискриминант характеристического квадратного уравнения положителен: D > 0. Тогда корни характеристического уравнения k₁ и k₂ действительны и различны. В этом случае общее решение описывается функцией

где C₁ и C₂ − произвольные действительные числа. 

2. Дискриминант характеристического квадратного уравнения равен нулю: D = 0. Тогда корни действительны и равны. В этом случае говорят, что существует один корень k₁ второго порядка. Общее решение однородного дифференциального уравнения имеет вид:

3. Дискриминант характеристического квадратного уравнения отрицателен: D < 0. Такое уравнение имеет комплексно-сопряженные корни k₁ = α + βi, k₁ = α − βi. Общее решение записывается в виде

39. . Линейные неоднородные диф уравнения второго порядка с постоянными коэффициентами

Структура общего решения

Линейное неоднородное уравнение данного типа имеет вид:

где p, q − постоянные числа (которые могут быть как действительными, так и комплексными). Для каждого такого уравнения можно записать соответствующее однородное уравнение:

Теорема: Общее решение неоднородного уравнения является суммой общего решения y₀(x) соответствуюшего однородного уравнения и частного решения y₁(x) неоднородного уравнения:

Ниже мы рассмотрим два способа решения неоднородных дифференциальных уравнений.

Метод вариации постоянных

Если общее решение y₀ ассоциированного однородного уравнения известно, то общее решение неоднородного уравнения можно найти, используя метод вариации постоянных.  Пусть общее решение однородного дифференциального уравнения второго порядка имеет вид:

Вместо постоянных C₁ и C₂ будем рассматривать вспомогательные функции C₁(x) и C₂(x). Будем искать эти функции такими, чтобы решение

удовлетворяло неоднородному уравнению с правой частью f(x).  Неизвестные функции C₁(x) и C₂(x) определяются из системы двух уравнений:

40. Система нормальных диф уравнений.

В дифференциальные уравнения вида

может входить n неизвестных функций x1,…, xn . Тогда системой дифференциальных уравнений будет совокупность соотношений

Предположим, что эту систему можно разрешить относительно старших производных. В этом случае получим систему уравнений:

Такая система называется канонической системой дифференциальных уравнений. Вводя новые неизвестные функции, можно привести эту систему к системе первого порядка. Пусть

Тогда наша система перепишется в виде

В дальнейшем будем рассматривать систему из n уравнений первого порядка в виде

Эта система называется нормальной (канонической) системой дифференциальных уравнений. Эту систему будем записывать в векторной форме:

Тогда данная система будет представлена в виде:

Решением этой системы на интервале G называется совокупность n функций xi=xi(t), определенных на интервале G и таких, что подстановка их в эту систему обращает каждое ее уравнение в тождество на всем интервале G.

Если вектор-функция не зависит явно от времени t, то эта система называется автономной (стационарной).

41. Числовой ряд, определение ,сходимость , свойства сходящихся числовых рядов.

Числовой ряд — это числовая последовательность, рассматриваемая вместе с другой последовательностью, которая называется последовательностью частичных сумм (ряда).