Действия с матрицами –1
A:=
rows(a)=2
cols(a)=3
Задание матрицы А с размерностью 2
3
B:=
B:=
Транспонирование матрицы А
M:=identity(2)
M=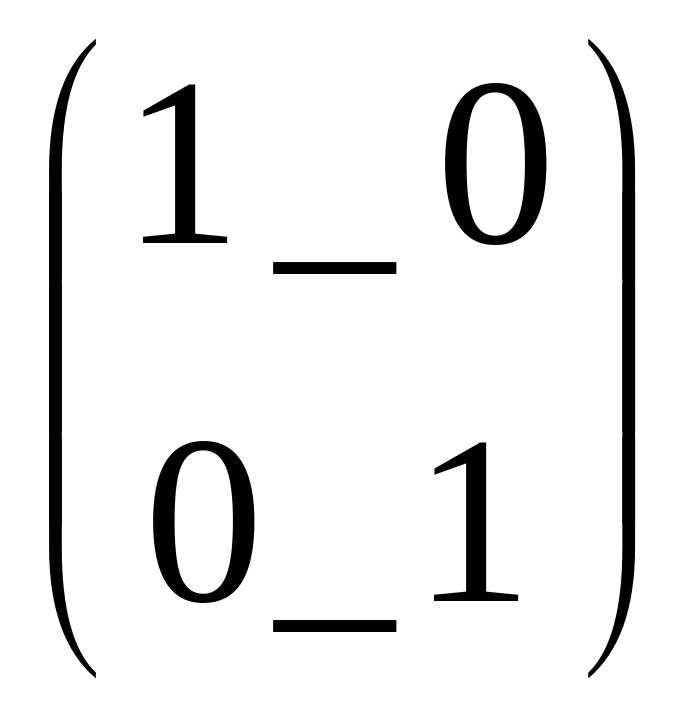
Создание единичной матрицы М
Tr(M)=2 Вычисление следа матрицы
A:=
B:=
B=
Задание и обращение матрицы А
C:=
С=
Повторное обращение
восстанавливает исходную матрицу (
матрица С=А)
A:=
B:=
A·B=
Умножение двух матриц
A:=
D:=
D=10
Задание квадратной матрицы А и
вычисление ее детерминанта
Действия с матрицами –2
V=
Выделение второго (отсчет с нуля)
столбца матрицы А
=4
=2
=3
Выделение элементов матрицы А
А:=
-A=
2·А=
Задание матрицы А, смена знака у всех
её
элементов, удвоение их и деление на два
А:=
В:=
А+В=
Суммирование двух матриц -Аи В
W
:=exp(V)
W=
Векторизация вектора W
I:=
A:=
Задание матрицы А с комплексными
элементами
M1:=
identity(3)
M1=
Задание и вывод единичной квадратной
матрицы М1
V:=
augment(M1,
V)=
Задание вектора V
и подключение его к ранее созданной
матрице М1
М2:=
augment(M1,M2)=
Задание матрицы М2 и подключение ее
к матрице М1
Tr(M1)=3 Вычисление следа матрицы М1: суммы диагональных эдементов
i:=
Задание матрицы СМ с комплексными элементами
CM:=
R:=Re(CM)
R=
Выделение матрицы- действительной
части матрицы СМ
J:=lm(CM) J=
Выделение матрицы- мнимой части
матрицы
K:=1..3
L:=1..3
:=
+
Восстановление матрицы с комплексными
элементами по матрицам R
и J
МС=
Вывод восстановленной матрицы
( МС=СМ)
3. Ранжированные переменные
До сих пор мы рассматривали переменные, которые имеют единственное значение. Однако в математике часто возникает необходимость в задании некоторого ряда значений – чаще всего упорядоченного. Например, для вычисления факториала N! = 12…(N-1)N нужно сформировать ряд чисел от 1 до N с шагом 1 и перемножить их. Также упорядоченный ряд значений какой-то переменной (например абсциссы x) нужен для построения графика функции – Mathcad строит графики функций по точкам, соединяя их по отрезкам прямых.
Для создания таких рядов в Mathcad используются так называемые ранжированные переменные. Иногда они заменяют управляющие структуры – циклы, однако полноценной такая замена всё же не является, в частности, потому что не предусмотрен выбор любого значения ранжированной переменной.
В самом простом случае для создания ранжированной переменной используется выражение: Name := Nbegin . . Nend, где Name – имя переменной, Nbegin – её начальное значение, Nend – конечное значение, .. – символ, указывающий на изменение переменной в заданных пределах (он вводится знаком точки с запятой ;). Если Nbegin < Nend, то шаг изменения переменной будет равен +1, в противном случае –1.
Для создания ранжированной переменной общего вида используется выражение: Name := Nbegin, (Nbegin + Step) . . Nend. Здесь Step – заданный шаг изменения переменной (он должен быть положительным, если Nbegin<Nend, или отрицательным в противном случае).
