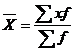16. Понятие вариации и задачи её изучения.

Вариация – это различие значений признака у отдельных единиц изучаемой совокупности в один и тот же период или момент времени. Вариация отражает колеблемость индивидуальных значений признака, отражает неравномерность развития единиц совокупности.

Стат. анализ вариации предполагает след. этапы: построение вар. ряда, его графич. изобр., расчет показ. центра распред. и структур. характеристик ряда, расчет показ. размера и интенсивности вариации, оценка вар.ряда на асимметрию и эксцесс.

Задачей статистики является оценка различий между явлениями. Оценка различий осуществляется с помощью показателей вариации, при этом расчет показателей может быть осуществлен по первичным данным (неосредненным) и по сгруппированным, представленным в виде рядов распределения. Ряд распределения – упорядоченное распределение единиц совокупности по возрастающим или убывающим значениям признака и подсчет единиц с тем или иным значением признака.

17. Вариационный ряд: понятие, виды вариационных рядов, порядок построения и оформления, графическое изображение.

Вариационный ряд – упорядоченное распределение единиц совокупности по возрастающим или убывающим значениям признака и подсчет единиц с тем или иным значением признака, ряд, построенный по количественному признаку, по качественному – атрибутивный. Бывает вар. ряд: дискретный (вырьирующий признак выражен целым числом) и интервальный (указываются интервалы). Элементы вариационного ряда: варианты (значения, которые принимает исследуемый признак), частоты (абсолютная численность отдельных групп с различными значениями признака), частости (удельные веса отдельных групп в общей численности совокупности).

Плотность распред – исп. вместо частот, если неравные интервалы. Абсолют. плотн = частота/ширину интервала, относит. плотность = частость/шир. интервала.

Порядок построения: 1. Определение числа интервалов.

2.Определение величины интервалов. i=(xmax-xmin)/k 3.Распределение ед. совок. по выдел. группам.

Графическое изображение: гистограмма (столбиковая диаграмма, на оси абсцисс которой откладывают отрезки, равные величине интервалов вар. ряда, на отрезках строят столбцы, их высота = частотам или частостям); полигон распределения – у столбиков соединяем середины прямыми линиями, последние сер. опускаем в точки на Х с разничей в ед. месштаба; кумулята – по накопл. Частотам(накопл. Частоты определяют поледовательность суммированием частот(частостей), они показыкают, сколько единиц совокупности имеют значение признака не больше,чем рассматриваемое значение. При построении кумуляты отсутствует нулевая частота, верхней-вся частота первого интервала и тд. Верхней границе последнего интервала-сумма накопленных частот частот во всех интервалах(100%))., огива- перевернутая кумулята; кр. Лоренца (по накопл. значениям).

18. Показатели центра распределения и структурные характеристики вариационного ряда(Мо,Ме, децили, квартили), использование их в статистическом анализе.

Для зарактеристики среднего значения признака в вариационном ряду используется так называемые показатели центра распределения. Кним относятся средняя величина признака,мода и медиана.

Расчет средней:

Средняя арифметическая взвешенная

Где х –варианты признака, f- частоты(частости)

При расчете средней величины интервального ряда в качестве вариантов признака используются значения середины интервалов. Для нахождения середины открытых интервалов необходимо их закрыть, т.е. определить недостающую верхнюю и нижнюю границы.Принято считать, что в первой группе величина интервала равна интервалу второй группы, а в последней – интервалу предыдущей.

Мода- значение признака,наиболее часто встречающееся в изучаемой совокупности. В дискретном ряду модой является вариант с наибольшей частотой(частостью). В интервальном вар ряду мода рассчитывается по формуле:

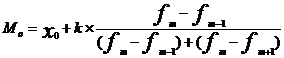, где х_о – нижняя граница модального интервала, f_m, f_m-1, f_m+1 – частоты соответственно модального,домодального и послемодального интервалов, k- величина модального интервала.

Модальный интервал – это интервал, имеющий наибольшую частоту( частость).

Медиана- вариант, расположенный в середине упорядоченного вариационного ряда, делящий его на две равные части, таким образом,что половина единиц совокупности имеют значения признака меньше,чем медиана,а половина – больше. Определяется по формуле:

Где х-начало медианного интервала, i – величина медианного интервала, 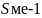- сумма накопленных частот в домедианном интервале, 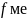- частота медианного интервала, ∑f – сума частот вар ряда.

Медианный интервал – интервал, в котором находится порядковый номер медианы. (необходимо подсчитать сумму накопленных частот до числа,превышающего половину объема совокупности.

По соотношению характеристик центра распределения можно судить о симметричности эмпирического ряда распределения.

Симметричный ряд: Хср=Мо=Ме

Левосторонняя асимметрия: Хср<Me<Mo

Правосторонняя асимметрия: Хср>Me>Mo

Мода и медиана – структурные средние(дают количественную характеристику структуры строения вариационных рядов), другие структурные характеристики: квартили – делят ряд на 4 равные части и определяются по формуле: , децили – делящие ряд на 10 частей.

Общая схема расчета децилей:

1. По накопленным частостям определяем интервалы,куда попадают порядковые номера децилей: для первой децили – интервал, где находится вариант, отсекающий 10% совокупности с наименьшими значениями признака, для второй – 20% и т.д., для девятой – 90% с наименьшими признаками или 10% с наибольшими признаками.

2. Рассчитываем величину децилей по формулам:

, …

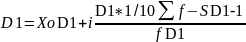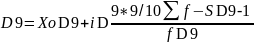
Коэффициент децильной дифференциации доходов населения: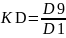

Он показывает во сколько раз совокупность с наибольшим значением признака превышает совокупность с наименьшим значением.