3. Уравнения, однородные относительно
Рассмотрим уравнения вида где F является однородной с показателем m относительно , т.е.
С
помощью замены
, где u - новая неизвестная функция,
порядок уравнения (4) понижается на
единицу. Имеем
,
,
Данная подстановка дает дифференциальное
уравнение (n-1) - го порядка относительно
новой неизвестной функции u:
.
4. Обобщенно - однородные уравнения.
Рассмотрим уравнения вида
Уравнение
(5) называется обобщенно - однородным,
если существуют числа k и m такие, что
С помощью замены (при x<0 полагаем
)
, где t - новая независимая переменная,
u - новая искомая функция, уравнение (5)
приводит к уравнению, не содержащему
независимой переменной t и, следовательно,
допускающему понижение порядка на
единицу (см. п. 2).
Производные при данной замене преобразуются по формулам
,
Подстановка
последних равенств в (5) дает уравнение
вида
которое явно не содержит независимую
переменную t.
5. Уравнение в точных производных.
Рассмотрим
уравнения вида
левые части которых являются точными
производными от некоторой функции
, т.е.
Такие уравнения называются уравнениями
в точных производных. Из последнего
равенства следует, что соотношение
является первым интегралом уравнения
(1) - уравнением (n-1) - го порядка относительно
искомой функции. Таким образом, уравнение
в точных производных допускают понижение
порядка на единицу.
Пример
5.
Решить уравнение
Решение.
Имеем
откуда следует, что
или
Это линейное уравнение первого порядка,
и его общее решение имеет вид
.
Вопрос 6. Линейные дифференциальные уравнения высших порядков. Существование и свойтства решений лоду. Теорема о структуре общего решения лоду. Решение лоду с постоянными коэффициентами.
Линейные дифференциальные уравнения высших порядков
Основные понятия
Многие задачи математики, механики, электротехники и других технических наук приводят к линейным дифференциальным уравнениям. Уравнение вида
где bo(x) ≠ 0, b1(x),..., bn(x), g(x) - заданные функции (от х), называется линейным ДУ n-го порядка.
Оно содержит искомую функцию у и все ее производные лишь в первой степени. Функции bo(x), b1(x),..., bn(x) называются коэффициентами уравнения (3.11), а функция g(x) - его свободным членом.
Если свободный член g(x)=0, то уравнение (3.11) называется линейным однородным уравнением; если g(x) ≠ 0, то уравнение (3.11) называется неоднородным.
Разделив уравнение (3.11) на bo(x) ≠ 0 и обозначив
запишем уравнение (3.11) в виде приведенного:
Далее будем рассматривать линейные ДУ вида (3.12) и считать, что коэффициенты и свободный член уравнения (3.12) являются непрерывными функциями (на некотором интервале (а;b)). При этих условиях справедлива теорема существования и единственности решения ДУ (3.12) (см. теорему. 3.1).
Линейное однородное дифференциальное уравнение n-го порядка с постоянными коэффициентами записывается в виде
где a1, a2,..., an − постоянные числа, которые могут быть действительными или комплексными.
Используя
линейный дифференциальный оператор
L(D), данное уравнение можно представить
в виде
где
Для каждого дифференциального оператора
с постоянными коэффициентами можно
ввести характеристический многочлен
Алгебраическое уравнение
называется
характеристическим уравнением
дифференциального уравнения.
Согласно основной теореме алгебры, многочлен степени n имеет ровно n корней с учетом их кратности. При этом корни уравнения могут быть как действительными, так и комплексными (даже если все коэффициенты a1, a2,..., an действительные).
Рассмотрим более детально различные случаи корней характеристического уравнения и соответствующие формулы общего решения дифференциального уравнения.
Случай 1. Все корни характеристического уравнения действительные и различные
Предположим,
что характеристическое уравнение L(λ)
= 0 имеет n корней λ1, λ2,..., λn. В этом случае
общее решение дифференциального
уравнения записывается в простом виде:
где C1, C2,..., Cn − постоянные, зависящие
от начальных условий.
Случай 2. Корни характеристического уравнения действительные и кратные
Пусть
характеристическое уравнение L(λ) = 0
степени n имеет m корней λ1, λ2,..., λm,
кратность которых, соответственно,
равна k1, k2,..., km. Ясно, что выполняется
условие
Тогда общее решение однородного
дифференциального уравнения с постоянными
коэффициентами имеет вид
Видно, что в формуле общего решения каждому корню λi кратности ki соответствует ровно ki членов, которые образуются умножением x в определенной степени на экспоненциальную функцию exp(λi x). Степень x изменяется в интервале от 0 до ki − 1, где ki − кратность корня λi.
Случай 3. Корни характеристического уравнения комплексные и различные
Если
коэффициенты дифференциального
уравнения являются действительными
числами, то комплексные корни
характеристического уравнения будут
представляться в виде пар
комплексно-сопряженных чисел:
В этом случае общее решение записывается как
Случай 4. Корни характеристического уравнения комплексные и кратные
Здесь каждой паре комплексно-сопряженных корней α ± iβ кратности k соответствует 2k частных решений
Тогда часть общего решения дифференциального уравнения, соответствующая данной паре комплексно-сопряженных корней, конструируется следующим образом:
В общем случае, когда характеристическое уравнение имеет как действительные, так и комплексные корни произвольной кратности, общее решение строится в виде суммы рассмотренных выше решений вида 1-4.
Пример 1
Решить дифференциальное уравнение y''' + 2y'' − y' − 2y = 0.
Решение.
Составим
соответствующее характеристическое
уравнение:
Решая его, находим корни:
Видно,
что все три корня действительные.
Поэтому, общее решение дифференциального
уравнения записывается в виде
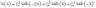
где C1, C2, C3 − произвольные постоянные.
Совокупность
частных линейно независимых решений
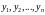составляет фундаментальную систему
решений ЛОДУ (3).
Тогда
общее решение ЛОДУ (12) имеет вид:
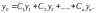
Компоненты общего решения дифференциального уравнения (3) определяются в зависимости от характера корней характеристического уравнения (4) следующим образом:
1)
каждому действительному простому (т.е.
не кратному) корню
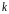в общем решении соответствует слагаемое
вида
;
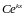2)
каждому действительному корню кратности
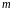в общем решении соответствует слагаемое
вида
;
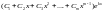3)
каждой паре комплексных сопряженных
простых корне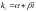й
и
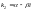в
общем решении соответствует слагаемое
вида
;
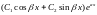каждой
паре комплексных сопряженных корне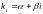й
и
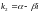кратности
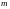в общем решении соответствует слагаемое
вида
.
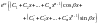