Двумерные непрерывные случайные величины

Определение: Двумерная случайная величина (X,Y) называется двумерной непрерывной случайной величиной, если пространством элементарных событий этой двумерной независимой случайной величины являются двумерная плоскость либо область двумерной плоскости, а X,Y-это одномерные непрерывные случайные величины.

, (так как X и Y- непрерывные случайные величины) - функция распределения двумерной величины (X,Y).

Найдем вероятность того, что в результате испытания над случайной величиной (X,Y) произошло событие:

попадание в элементарный прямоугольник с вершиной в точке (х, у) и сторонами , параллельными осями координат.

Вероятность этого события равна:

=

Так как данный прямоугольник принадлежит Борелевской алгебре, его вероятность существует.

y

y

0 x x

Определение: Двумерной плотностью вероятности двумерной непрерывной случайной величины (X,Y) называется числовая скалярная функция двух действительных аргументов, которая при фиксированных значениях своих аргументов численно равна пределу, если он существует

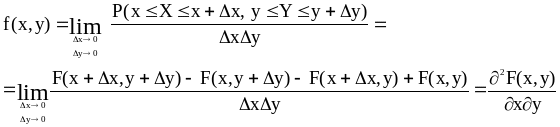
Из этого определения очевидным образом вытекает второе определение:

Найдем вероятность попадания непрерывной случайной величины в некоторую область пространства элементарных событий:

y

G

0 x

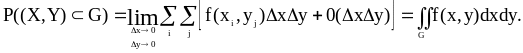
Определим двумерную функцию распределения через двумерную плотность вероятности.

1. Эта функция возрастает, при возрастании каждой из переменных х и у;

2. Стремится к единице, когда оба аргумента неограниченно возрастают.

Тогда:

Пример: равномерное распределение двумерной случайной величины

Вычисление одномерных плотностей вероятности по двумерной плотности вероятности

Имеется непрерывная случайная величина (X,Y) и плотность f(x,y). Требуется найти одномерные плотности f _X(x) и f_Y(y) и функции распределения.

Вычислим f_X(x).

Согласно общей формуле, найдем:

Так как полученные равенства верны при произвольных значениях внешнего предела, то верны их подинтегральные выражения, т.е. плотность величины X:

.

Аналогично показать самим, что:

.

Условные плотности вероятности

Условной плотностью Y при заданном значении X=x называется функция, которая удовлетворяет следующим условиям:

Выражение для условной плотности вероятности не выводится, а задается (так как не выводится формула условной вероятности) в виде:

,

где y-аргумент, x-число

Можно дать лишь обоснование данной формулы:

Рассмотрим события: , .

Тогда

Линии регрессии Y по X и X по Y определяются теперь как условные математические ожидания:

,

.

Условные дисперсии:

Функции и называются линиями регрессии.

Обозначим

Тогда

Доказательство: