1). Поняття функції двох змінних.Означення

Якщо кожній парі (Х, у) значення два, незалежних один від одного, змінних величин Х і У, з деякої області їх зміни D, відповідає певне значення величини U, то говорять, що U Є функція двох змінних Х і У, визначена в області D

2).Область визначення функцій двох змінних.

Сукупність пар (Х, у) значень Х і У, при яких визначається функція U = f(x, у), називається областю існування або областю визначення цієї функції. При цьому пара (Х, у) визначає крапку в області існування.

3).Частинні і повний прирости функцій двох змінних.

Різниця називається повним приростом функції , а різниці

називаються частинними приростами функції по х і по у відповідно.

4). Частинні похідні.Означення,Геометричий зміст Похідна функції при називається частинною похідною по х функції у точці і позначається

,

а похідна функції при називається частинною похідною по у функції у точці і позначається

5).Частинні похідні складної функіції

Нехай 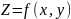  – функція двох змінних x та y, кожна з яких, у свою чергу, є функцією незалежної змінної t:

тоді функція   є складеною функцією змінної t.

6).Частинні похідні вищих порядків

Нехай функція   має частинні похідні в усіх точках множини D. Візьмемо будь-яку точку   . Якщо в цій точці існують частинні похідн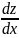і   і   , то вони залежать від х і у, тобто вони є функціями двох змінних. Отже, можна ставити питання про відшукання їх частинних похідних. Якщо вони існують, їх називають частинними похідними другого порядкуі позначають відповідно   або   ,   аб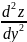о   ,   або   ,   або   .

7).Екстремум функції двох змінних. Умови існування екстремуму

Нехай функція z=f(x;y) визначена в деякій області точки (х0,у0). Кажуть, що функція z=f(x;y) має в точці (х0,у0) строгий максимум (мінімум), якщо f(x;y)f(x0;y0)) для всіх точок (х;у), достатньо близьких до х0, у0. Точка (х0,у0) – точка максимуму (мінімуму). Максимум і мінімум функції називають екстремумами функціями. Необхідні умови екстремуму. У точці екстремуму диференційовної функції багатьох змінних її частинні похідні дорівнюють нулю, тобто

З цієї системи рівнянь знаходять стаціонарні точки.

8).Найбільше і найменше значення функції двох змінних

Якщо функція f (x, y, ...) визначена і неперервна в замкненій і обмеженій області D, то в цій області знайдеться, принаймні, одна точка

N (x 0 , y 0 , ...), така, що для решти точок вірно нерівність

а також точка N 1 (x 01 , y 01 , ...), така, що для всіх інших точок вірно нерівність

f (x 01 , y 01 , ...) ВЈ f (x, y, ...)

тоді f (x 0 , y 0 , ...) = M - найбільшу значення функції, а f (x 01 , y 01 , ...) = m -найменше значення функції f (x, y, ...) в області D.

Безперервна функція у замкненій та обмеженій області D досягає по Принаймні один раз найбільшого значення і один раз найменшого.

9). Диференціальні рівняння — це рівняння виду  , де   — невідомафункція (можливо, вектор-функція; в такому випадку часто говорять про систему диференціальних рівнянь), що залежить від змінної часу  , штрих означає диференціювання по  . Число   називається порядком диференціального рівняння.

Розв'язком (або рішенням) диференціального рівняння називається функція, що диференціюється n разів, і задовольняє рівнянню в усіх точках своєї області визначення. Зазвичай існує ціла множина таких функцій, і для вибору однієї з них на розв'язок потрібно накласти додаткові умови: наприклад, вимагати, щоб рішення приймало в певній точці певне значення.