Математиканың даму тарихы Математика (грек.mathematike- білім, ғылым)- ақиқат дүниенің сандық қатынастары мен кеңістік формалары жайлы ғылым. Көрнекті совет математиктері А. Н. Колмогоров пен А. Д.Александров ұсынған жіктеу бойынша математиканың даму тарихы шартты түрде төрт кезеңге бөлінеді. Бірінші кезең- математиканың білім- дағдыларының қорлану, жинақталу дәуірі. Ол ерте кезден басталып б.з.б. 7-6 ғасырларына дейін созылды. Бұл дәуірде математика адамзат практикасы мен тәжірибесіне тікелей тәуелді болды, солардан қорытылған ережелер жинағынан тұрды. Екінші кезең- математиканың өз алдына дербес теориялық ғылым болып туу, қалыптасу кезеңі. Мұнда арифметика, геометрия, алгебра, тригонометрия айрықша теориялық пән болып қалыптасты. Бұл кезең тұрақты шамалар математикасының, кейде элементар математика кезеңі деп аталады. Ол екі мың жылға жуық мерзімге созылып, шамамен 17 ғасырда аяқталады. Үшінші кезең- айнымалы шамалар математикасы немесе жоғары математиканың туу, қалыптасу кезеңі. Бұл 17 ғасырда басталып, 19 ғасырдың 2-жартысына дейін созылды. Жиындар теориясына байланысты анализдің, геометрияның және алгебраның жаңа сападағы салалары шыққаннан кейін, математиканың негізгі мәселелерін жалпы қарастыру кезеңін төртінші кезеңге жатқызуға болады. Ол- 19-20 ғасырларды қамтитын қазіргі математика кезеңі.

Жазықтықтағы координаттар әдісінің негізгі идеясы – L сызығының геом. қасиеттерін осы сызықты сипаттайтын Ғ (х, у) = 0 теңдеуін аналит. және алгебр. жолмен зерттеу. Жазықтықтағы А. г-да 1- және 2-реттік алгебр. сызықтар жүйелі түрде зерттеледі. 1-реттік сызықтар – түзу сызықтар және олар бір дәрежелі Ах + Ву + С = 0 алгебр. теңдеуімен, ал 2-реттік қисық сызықтар Ах2 + Вху + Су2 + Dх + Еу + Ғ = 0 теңдеуімен сипатталады. 2-реттік қисық сызықтарға эллипс, гипербола, парабола қисықтары жатады. Табиғатта өте жиі кездесетін бұл қисықтардың негізгі қасиеттері А. г-да толық анықталған. Кеңістіктегі А. г-да координаттар әдісі жазықтықтағы әдіске толық ұқсас етіп қарастырылады. Мұнда кез келген М нүктесі х – абсцисса, у – ордината және z – аппликата координаттары арқылы анықталады. Кеңістікте орналасқан S бетін Oxyz координаттар жүйесіне қатысты F = (x, y, z) = 0 теңдеуімен сипаттауға болады. Кеңістіктегі А. г-да Ах + Ву + Сz + D = 0 теңдеуімен анықталатын 1-реттік беттердің (жазықтықтардың) және Ах2 + Ву2 + Сz2 + Dху + Еуz + Ғхz + Gх + Ну + Мz + N = 0 теңдеуімен анықталатын 2-реттік беттердің (эллипсоидтың, гиперболоидтың, параболоидтың) қасиеттері зерттеледі.

Аффиндык координат жүйесі.Кез келген үш нүктенің коллинеарлық шарты сақталып, бір мәнді кеңістіктің нүкетлік түрленуі аффиндық түрлендіру деп аталады. Бұл түрлендіруде үш коллинеарлық нүкте үш коллинеарлық нүктелерге көшеді.

Аффиндық түрлендірудің негізгі қасиеті мынау: кеңістіктің кезе келген аффиндық түрленуі сызықтық түрленуге жатады. Аффиндық түрлендірудің қасиеттері мынадай:

1. өз ара коллинеар болмайтын кеңістіктің үш нүктесі коллинеар емес үш нүктеге,

2. өз ара компланар болмайтын төрт нүкте компланар емес төрт нүктеге,

3. түзу сызық түзу сызыққа,

4. қиылысатын екі түзу қиылысатын екі түзуге

5. бір параллелограмның төрт төбесі екінші параллелограмның төрт төбесіне,

6. бір кесіндінің ортасы екінші кесіндінің ортасына

7. кеңістіктегі кез келген бір М нүктесі екінші бір М ^’ нүктесінде көшеді. Бұл екі нүктенің әрқайсысы өзіне сәйкес координаталар системасында анықталады.

Егер осы айтылған қасиеттер сақталса, онда мұндай ұғымды аффиндік түрлендіру дейміз. Басқаша айтқанда, еркінше алынған аффиндік түрлендіруде сақталатын геометриялық бейнелердің қасиеттерін аффиндік түрлендіру дейміз. Мысалы, параллелограм, түзу сызық, эллипс, гипербола, парабола аффиндік ұғымға жатады. ал тік бұрышты төртбұрышты, шеңбер аффиндік ұғымға жатпайды. Өйткені аффиндік түрленуде тік бұрышты төртбұрыш параллелограмға ал шеңбер эллипске айналады. Сондықтан бұл екі пішін аффиндік ұғым болмайды. Сонымен түрлендірілгеннен кейін теореманың қасиеті сақталса, онда мұндай теорема аффиндік деп аталады. Мысалы, үш медиана бір нүктеде қиылысады деген теорема аффиндік болады, ал үш биссектриса бір нүктеде қиылысады деген теорема аффиндік теоремаға жатпайды. Аффиндік ұғымдар мен теоремалардың жиындысын аффиндік геометрия деуге болады. Аффиндік геометрияда кесіндінің ұзындығы деген ұғым жоқ. Мұнда кез келген кесіндіні координаталық вектор деп қабылдауға болады. Аффиндік түрленудегі координаталық вектор ұзындығы еркінше алынатын кез келген вектор болуы мүмкін. Осы сияқты аффиндік геометрияда аудан мен көлем де анықталмайды.

Математиканың даму тарихы Математика (грек.mathematike- білім, ғылым)- ақиқат дүниенің сандық қатынастары мен кеңістік формалары жайлы ғылым. Көрнекті совет математиктері А. Н. Колмогоров пен А. Д.Александров ұсынған жіктеу бойынша математиканың даму тарихы шартты түрде төрт кезеңге бөлінеді. Бірінші кезең- математиканың білім- дағдыларының қорлану, жинақталу дәуірі. Ол ерте кезден басталып б.з.б. 7-6 ғасырларына дейін созылды. Бұл дәуірде математика адамзат практикасы мен тәжірибесіне тікелей тәуелді болды, солардан қорытылған ережелер жинағынан тұрды. Екінші кезең- математиканың өз алдына дербес теориялық ғылым болып туу, қалыптасу кезеңі. Мұнда арифметика, геометрия, алгебра, тригонометрия айрықша теориялық пән болып қалыптасты. Бұл кезең тұрақты шамалар математикасының, кейде элементар математика кезеңі деп аталады. Ол екі мың жылға жуық мерзімге созылып, шамамен 17 ғасырда аяқталады. Үшінші кезең- айнымалы шамалар математикасы немесе жоғары математиканың туу, қалыптасу кезеңі. Бұл 17 ғасырда басталып, 19 ғасырдың 2-жартысына дейін созылды. Жиындар теориясына байланысты анализдің, геометрияның және алгебраның жаңа сападағы салалары шыққаннан кейін, математиканың негізгі мәселелерін жалпы қарастыру кезеңін төртінші кезеңге жатқызуға болады. Ол- 19-20 ғасырларды қамтитын қазіргі математика кезеңі.

Ықтималдықтың классикалық анықтамасы

Ықтималдықтар теориясының негізгі ұғымдарының бірі-оқиға. Егер белгілі бір шарттар жиынтығы орындалғанда болатын немесе болмайтын оқиға кездейсоқ деп аталады. Оқиға сынақ нәтижесі деп қарастырылады.

Анықтама. Оқиға ықтималдығы деп осы оқиға орындалуына қолайлы элементар жағдайлар санының осы сынақтағы барлық толық топ құрайтын бірдей мүмкіндікті, тең мүмкіндікті үйлесімсіз жағдайлар санына қатынасын айтамыз:

мұндағы n-барлық сынақтардың жалпы саны, m - А оқиғасы орындалатын сынақтар саны.

Ақиқат оқиға ықтималдығы p=1. Анықтамаға сүйенсек, А – ақиқат оқиға болғандықтан m=n болады да

P(A)=1.

Жалған оқиғаның ықтималдығы p=0. Бұл жағдайда анықтамаға сүйенсек, m=0 болады да

Кездейсоқ оқиға ықтималдығы 0 мен 1- дің аралығында анықталады:

0<P(A)<1

Сонымен, кез келген оқиғаның орындалу ықтималдығы 0≤P(A)≤1 теңсіздігін қанағаттандырады.

А және В оқиғаларының қосындысыдеп А оқиғасының орындалуын, немесе В оқиғасының орындалуын, немесе А және В оқиғаларының екеуініңде орындалуын айтамыз және былай белгілейміз А+В.

А және В оқиғаларының көбейтіндісідеп А мен В оқиғалары бірлесе орындалатын А·В оқиғасын айтамыз.

Егер А оқиғасының орындалуы В оқиғасының да орындалуын қамтамасыз етсе, онда А оқиғасы В оқиғасының құрамында жатады деп айтамыз, және былай белгілейміз АÌВ.

Егер АÌВ болса, онда А·В=А және А+В=В екендігі жоғарыдағы анықтамалардан шығады.

А және В оқиғаларының айырмасы деп А оқиғасы орындалып, В оқиғасы орындалмайтын оқиғаны айтамыз және С=A\B немесе C=A-B деп белгілейміз.

Сынақ нәтижесінде орындалған А оқиғасы В оқиғасының да орындалуын қамтыса (яғни, АÌВ) немесе осы сынақта В оқиғасының орындалуы А оқиғасының да орындалуын қамтыса (яғни ВÌА), онда А және В оқиғалары балама (эквивалент) деп аталады және А=B деп белгіленеді. Өзара балама оқиғалар теңбе-тең немесе тең оқиғалар деп аталады.

Белгілі бір шарттар жиыны іске асырылғанда, міндетті түрде орындалатын оқиға ақиқат оқиға деп аталады

Белгілі бір шарттар жиыны іске асырылғанда, алдын ала орындалмайтыны белгілі оқиға жалған оқиға деп аталады

Ақиқат оқиғаны U деп , жалған оқиғаны V деп белгілейміз.

Егер бір сынақта бір оқиғаның орындалуы басқа оқиғалардың орындалуын жоққа шығарса, онда оқиғалар үйлесімсіз деп аталады.

Егер А және В оқиғалары үйлесімсіз болса, онда А·В=V.

Қарама қарсы оқиғалар деп, толық топ құрайтын жалғыз мүмкіндікті екі оқиғаны айтамыз. Біреуі А оқиғасы деп, екіншісі   деп белгіленеді.

Ендеше, осы анықтамаларға сүйене отырып, төмендегі теңдіктерге оңай көз жеткізуге болады:

А+А=А А·А=А А+   =U A·   =V

A+V=A A·V=V A+U=U A·U=A

Оқиғалардың қосындысы, көбейтіндісі және айырмасының анықтамаларын қолдана отрып,мына төмендегі теңдіктерге көз жеткізуге болады:

АÈА=А АÇА=А АÈВ=ВÈА

АÇВ=ВÇА АÈ(ВÈС)=(АÈВ)ÈС АÇ(ВÇС)=(АÇВ)ÇС

А\В=АÇ   АÇ(ВÈС)=АÇВÈАÇС (АÈВ)Ç(АÈС)=АÈВÇС

   

 

Шешуі «нешеу», «неше тәсілмен» деген сұрақтарды қажет ететін есептер комбинаторикалық есептерделінеді. Мұндай есептерді шешумен айналысатын математика саласы комбинаториканемесекомбинаторикалық математика деп аталады.

1- анықтама. Берілген әртүрлі n элементтен m элемент бойынша орналастырулар деп әрқайсысы бір бірінен құрамы бойынша , немесе орналасу реті бойынша ажыратылатын комбинацияларды айтамыз.

 (2.1)

мұндағы n! ( эн факториал) дегеніміз n!=1· 2 ·3 ·4 ·5 · …· n 1-ден n-ге дейінгі натурал сандардың көбейтіндісі

Ескерту: 0!=1 деген ұйғарым алынған.

Мысал 1.2.1: Әр түсті 6 жалаушадан екеуден ала отырып, неше түрлі белгі беруге болады?

Шешуі: Есеп шартына сәйкес элементтер орналасу реті де, құрамы бойынша да ажыратылатын болғандықтан, орналастыру қолданылады:

Жауабы:30

2 - анықтама. Берілген әртүрлі n элементтен m элемент бойынша алмастырулар деп әрқайсысы бір бірінен тек орналасу реті бойынша ажыратылатын комбинацияларды айтамыз.

P_n =   = n!яғни

P_n = n!

Мысал 1.2.2: Егер 1, 2, 3 сандарынан әрбір сан кескінге бір рет енетін болса, неше үш орынды сан құруға болады?

Шешуі: Есеп шартына сәйкес элементтер тек орналасу реті бойынша ғана ажыратылатындықтан, алмастыру қолданылады:

Жауабы: 6

3 - анықтама. Берілген әртүрлі n элементтен m элемент бойынша терулер деп әрқайсысы бір бірінен тек құрамы бойынша ажыратылатын комбинацияларды айтамыз.

Мысал 1.2.3: Жәшіктегі 10 детальдан 3 детальды неше әдіспен алуға болады?

Шешуі:Есеп шартына сәйкес элементтер құрамы бойынша ажыратылғантықтан теру қолданылады:

Жауабы: 120

Аксиоматикалық әдіс. Мәнді және формальды теориялар, аксиомалар жүйесі, интерпритациясы.

Аксиоматикалық әдіс ғылыми теорияларды құру әдістерінің бірі. Белгілі бір ғылыми теорияны ғылыми әдіспен құру деп, аксиомалар жүйесінде алдын ала белгіленген логикалық ережелер бойынша теоремаларды алуды айтады. Аксиоматикалық әдістің даму 3 кезеңнен өтті: мәнді, формальді, аксиомалар жүйесі. Ерте кезде ғылымды аксиомаландыру оның тілін емес, қайта тұтас геометриялық білімді қамтиды. Аксиоматикалық әдісті осылайша түсінуді, мазмұнды(мәнді) аксиоматика д.а.Мәнді аксиоматиканың кемшіліктері ашылғаннан соң, ол математика ғылым дамуында басқадай жетілген аксиоматикамен ауыстырылды. ХІХғ бастап математикамен логиканы негіздеуге байланысты формальді аксиоматика п.б. осыдан Евклидтік емес геометрия п.б. Аксиом теорияның пәні ретінде оның кез келген түсіндірмелерін(интерпритацияларын) немесе моделін қарастыруға болады. Гедель бүкіл математика үшін тұтас аксиоматика жүйесін құруға және матем.білім түгіл ариф толық формальдауға және аксиомаландыруға мүлде болмайтындығын тамаша дәлелдеді. А.ә.бар білімді жүйеге келтіруге және жаңа теориялар жасап шығару үшін қажет. Ол матем теорияларды біріктіріп, олардың ортақ элементтерін табуға көмектеседі. Соңғы жылдары а.ә. физиканың жаңа салаларында теориялық биологияда, лингвистикада, касмологияда жиі қолданылады.

Жиын ұғымы. Жиындарға қолданылатын амалдар

  Жиын ұғымы математиканың негізгі ұғымдарының бірі болып табылады. Өзара әртүрлі (бөлек) заттарды қандай да бір қасиеті бойынша біріктіріп, бүтін бір зат ретінде қарастыруға болады. Алынған жаңа зат жиын деп, ал оның құрамындағы заттардың әрқайсысы жиынның элементі деп аталады. Жиынның элементтерінің саны ақырлы (шектеулі) да, ақырсыз (шектеусіз) да бола алады. Жиынды көбінесе латын алфавитінің үлкен (бас) әріптерімен, ал оның элементтерін кіші әріптермен белгілейді. 

Х жиынының x₁,x₂,..x_n элементтерінен тұратындығы X={x₁,x₂,…x_n} түрінде бейнеленеді. 

Жиын туралы айтқанда кез келген нәрсеге байланысты келесі екі мәселенің біреуі ғана орындалады: не нәрсе бұл берілген жиынға тиісті, не нәрсе бұл берілген жиынға тиісті емес. 

х заты X жиынының элементі болатыны xєX символымен белгіленеді

х заты X жиынының элементі болмайтыны xȼX символымен белгіленеді

Жиынның өзі ешқашан өзінің элементі болмайды: А ȼ А. 

Бірде-бір элементі жоқ жиынды бос (құр) жиын деп атайды да, Ø символымен белгілейді. 

А және В жиындары берілген болсын. Егер А жиынының әрбір элементі В жиынының да элементі болса, онда А жиыны В жиынының ішкі жиыны (жиыншасы) деп аталып, былайша белгіленеді: A B немесе AﬤB. 

Мұндай қатынас енгізу (ену) деп аталады. 

Егер A B және B C болса, онда A C .  

Кез келген жиын өзінің ішкі жиыны болып табылады: A A . 

Құр жиын кез келген A≠Ø жиынының ішкі жиыны болады:  Ø A . 

А B жиынының құр емес В ішкі жиыны А жиынымен дәлме-дәл келмейтін болса, онда оны меншікті ішкі жиын деп атайды. А жиынының А және Ø ішкі жиындарын оның меншікті емес ішкі жиындары деп атайды. 

Егер А жиынының элементтерінің саны n болса, онда оның ішкі жиындарының саны 2ⁿ болады. А жиынының барлық ішкі жиындарының жиынын А жиынының булеаны деп атайды. Белгілеуі B(A) . Сонда B(A)={X\X A} . 

Егер А және В жиындары үшін A B және B A кірістірулері бірдей орындалса, яғни бірінің кез келген элементі екіншісіне де тиісті болса, онда А және В жиындары тең дейді де, А=В символымен белгілейді. Басқаша айтқанда, егер А және В екі жиын бірдей элементтерден тұратын болса, онда оларды тең жиындар деп атайды және А=В деп жазады. Элементтерінің орындарын ауыстырғаннан жиын өзгермейді. 

1. Жиындардың бірігуі. Екі жиынның бірігуі. A және B жиындарының ең болмағанда біреуіне тиісті элементтерден, тек сол элементтерден ғана тұратын жиынды A және B жиындарының бірігуі деп атайды да, символымен AUB белгілейді:

AUB= {x: x A немесе x } .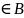 

Жоғарыдағы тәсілмен үш және одан да көп жиындардың бірігуін анықтауға болады.  

Егер A болса, онда A B=B болады, бұдан дербес жағдайда A A=A . 

2. Жиындардың қиылысуы. Екі жиынның қиылысуы. А және В жиындарының екеуіне де тиісті элементтерден тұратын жиынды А және В жиындарының қиылысуы деп атайды да, A B символымен белгілейді:A B={x: x A және x B}. Егер А және В жиындарының бір де бір ортақ элементі болмаса, яғни бұл екі жиын қиылыспайтын болса, онда A B=Ø. Бұл жағдайда А және В жиындары қиылыспайды деп те атайды. 

Жоғарыдағы тәсілмен үш және одан да көп жиындардың қиылысуын анықтауға болады.  

Егер A B болса, онда A B=A болады, дербес жағдайда A A=A . 

3. Екі жиынның айырмасы. А жиынына тиісті, ал В жиынына тиісті емес элементтерден тұратын жиынды А және В жиындарының айырмасы деп атайды да, A-B символымен белгілейді. А және В жиындарының айырмасын A-B символымен қатар A\B символымен де белгілейді. A-B={x:x A және x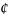 B} немесе A\B=={x\ x A және x B} . 

Егер A B және A≠B болса, онда A-B= Ø. 

1-теорема. A (B C)=(A B) . 

2-теорема. A (B-C)=(A B)-(A C). 

Егер A B және A≠B болса, онда B-A анықталған және бұл айырма келесі пунктте анықталатын толықтауыш жиын болады. 

4. Әмбебап жиын. Жиындар теориясында жеткілікті дәрежеде ауқымды жиынды алып, оның көлемінен шығып кетпейтіндей бекітілген жиынды алып қарастырады да, ол жиынды әмбебап (универсал) жиын деп атайды. Қарастырылатын жиындардың барлығының барлық элементтері осы әмбебап жиынға тиісті деп есептеледі, яғни қарастырылатын жиындардың барлығы да осы әмбебап жиынның ішкі жиындары болады. Әмбебап жиынды U символымен белгілеу келісілген. 

Кез келген жиынды графикалық түрде кескіндеуге болады. Ол үшін тұйық контур сызамыз да, жиынның элементтері осы контурдың ішіндегі нүктелермен кескінделген деп түсінеміз. Суретте нүктелерді жекелеп көрсету міндетті емес. Универсал жиын тіктөртбұрыш түрінде, оның ішкі жиындары осы тіктөртбұрышта жататын тұйық контур ретінде кескінделеді. Жиындарды бұл түрде кескіндеу Эйлер-Венн диаграммалары деп аталады. Көп жағдайда сыртқы төртбұрышты сызбайды, универсал жиынды атап көрсетпейді. 

Бөлінгіштік қатынас қасиеттері. Қалдықпен бөлу туралы теорема. Жай сандар, жай сандар жиынының шексіздігі. Эратосфен торы.

Z = {…-3, -2, -1, 0,1,2,3,...} бүтн сандар берілсін, бүтін сандарға қосу, азайту, көбейту, және бүтін санның модулінің ұғымы белгілі деп есептеп, бүтін сандардың бөлінгіштік қасиеттерін қарастырайық.

А: а,в, = 0 бүтін сандары үшін с бүтін саны табылып а = в*с орындалса, онда а бүтін саны в бүтін санына бөлінеді дейді. (а-бөлгіш, в-бөлгіш, с-бөлінді)

Егер а в-ға бөлінсе, а/в жазамыз. Егер в саны а-ны бөледі десек, онда в/а деп белгілейміз, а:в қатынасы бинарлық қатынас.

Қасиеттері:

1. Кез келген c € Z үшін а:аирефлексивтік, шындығында а = a*1

2. Кез келген а,в,с € Z а: в және в:с = > а:с – транзитивтік қасиет

3. Егер а:в, онда (-a):в, а:(-в), (-а):(-в)

4. Егер а:с және в:с, онда (а±в):с

5. Егер а:с және в € Z болса, онда (a*в):с

1-салдар. Егер а₁:с, ... а_n:с болса, онда кез келген r, … r€ Zүшін (ra+ra):с

2-салдар. Егер а₁, ... а_n, в_1, ..., в_m c-ға бөлінсе, және r1, …r n, s1, … , sm € Zболса, онда r₁a₁+r_na_n=s₁b₁+…+b_ms_m + b_m+1. Осыдан b_m+1:c шығады.

6. Егер а:с, в с – ға бөлінбесе, онда а±в с-ға бөлінбейді.

7. 0 саны кез келген в≠0 санына бөлінеді (a=в*0)

8. Кез келген а саны 1-ге бөлінеді (a=a*1)

9. Егер а ≠ 0 болса, онда 0*q=a орындалатын q саны табылмайды.

10. Егер а:в онда |а| ≥ |в|

1-салдар. Егер 1:а болса, онда а=1 немесе а=-1.

Дәлелдеу. Егер 1:ф болса, онда 1≥|а|, а ≠ 0 бүтін сан болғандықтан |а| ≥ 1, |а| = ±1

2-салдар. Егер а:в және в:а болса, онда а = в немесе а = -в

Дәлелдеу. а:в => |а| ≥ |в|, ал в:а |в| ≥|а| => |а| = |в|. Осыдан а = -в немесе а=в.

А:А бүтін санын b ≠0 санына калдық арқылы бөлу дегеніміз

A=bq+r, 0 ≤ r < |b| шарттарын қанағаттандыратын q, r, бүтін сандарын табу болады (q-толық емес бөлінді, r – қалдық)

Т: Егер а және b≠0 бүтін сандар болса, онда a-ны b-ға қалдық арқылы бөлуге болады және бөлу бір ғана тәсілмен орындалады.

Дәлелдеу:

1. А-кез келген бүтін сан, b>0. b-ға еселі сандарды өсу ретімен орналастырайық: ... b(-2), b(-1), b*0, b*16, b*2…

bq а-дан аспайтын ең үлкен сан болсын. а≥bq, a<b(q+1), яғни bq ≤ a <b(q+1). 0 ≤ a-bq + r, 0 ≤ r <|b|аламыз.

2. А бүтін сан, b< 0 болса, онда –b> 0. 1 – жағдай бойынша а-ны b – ға бөлуге болады. А = (-b)q+r, 0 ≤ r < |-b| a=b(-q) + r, 0 ≤ r < |b|

Меншікті бөлгіштері болмайтын бүтін р санын жай сан деп атайды. Жай санның 2 бөлгіші болады: 1 саны және сол санның өзі.

Т: егер р-жай сан болса, онда кез келген а саны мен р санына бөлінеді, не р –мен өзара жай сан болады.

Т: егер екі немесе бірнеше бүтін сандардың көбейтіндісі жай санға бөлінсе, онда бұл санға көбейткіштердің кемінде бірейі бөлінеді.

Евклид теоремасы. Натурал сандар қатарында шектеусіз көп жай сандар болады. Мұны дәлелдеу үшін кері жору тәсілін қолданады. Айталық, натурал сандар қатарындағы жай сандардың саны шектеулі сан делік және оларды р₁, р₂, ... р_n деп белгілейік. Мынадай сан

P = p₁p₂… p_n+1

Құрайық, бұл санның жай р₁, р₂, ... р_n сандарының ешбіріне де бөлінбейтінін байқаймыз, өйткені екінші 1 қосылғышы оларға бөлінбейді. Сондықтан р саны не құрама болуы тиіс, не жай сан болуы тиіс. Р жай сан бола алмайды, өйткені былай болғанда ол барлық р₁, р₂, ... р_n сандардан өзгешще бола тұра,(n+1) – ші жай сан болған болар еді, бұл біз жасағакн ұйғарымға қайшы. Алайда р саны құрама сан да бола алмайды, өйткені былай болғанда теорема (1 ден өзгеше кез келген құрама санның тең кіші бөлгіші жай сан болады) бойынша, барлық р₁, р₂, ... р_n сандардан өзгеше жай р бөлгіші болған болар еді, бұл да біз жасаған ұйғарымға қайшы. Міне, осы жағдай жай сандардың саны шектеулі болуы мүмкін емес екенін дәлелдейді.

Евклид теоремасын тағы былай тұжырымдауға болады: айырымы 1-ге тең шектеусіз арифметикалық прогрессия курамында шексіз көп жай сандар болады.

Натурал қатардан жай сандарды бөлу үшін Эратосфен торы деп аталатын тәсіл бар. Эраторфен тәсілі мынадай қарапайым жағдайға негізделген: өзінен кіші жай сандардың ешқайсысымен де еселік емес сан қалай да жай сан б.т.

Натурал қатарын жазайық:1,2,3,4,5,6,7,8,9,10, ...

Енді 2-нің өзіне тимей, 2 ге еселік сандардлың барлығын жазайық, сонда 2 ден бастап санағанда әр келесі екінші санды, яғни 4,6,8,10,.. сандарды сызып шығамыз. 2 – ден кейінгі сызылмай қалған 3 саны алдыңғы жасалған ескертуге қарағанда қалай да жай сан болмақ. Енді қатардағы қалған сандардың ішінен 1,2,3,5,7,9,11,13, ... 3-тің өзіне тимей, 3-ке еселік сандарды сызып шығамыз, сонда біз 9,15,21,... сандарды аламыз. Осылай сандар қатарынан екі рет сызып шыққанда сызылмай қалған келесі 5 саны да сол ескертпе бойынша жай сан болмақ.енді сол 5 тен бастап санап әр бесінші санды, яғни 5 ке еселік сандарды сызып шығамыз. 5 тен кейінгі енді сызылмай қалған 7 саны, бұл 7 ден кем әр 2,3,5 жай сандардың қай қайсысына да бөлінбейді, демек ол жай сан.

Құрама сандарды әрі қарай да осылай сызу процесін орындай келе біз натурал қатардың барлық жай сандарын табамыз.

Сандар жиынын кеңейту (N, Z, Q, R, C)

Сан және фигура ұғымдары басқа ешқайдан емес, тек шындық дүниеден алынған. Санау үшін саналуға тиісті нәрселердің ғана емес, сонымен бірге бұл нәрселерге көз жібергенде олардың сонымен басқа қасиеттеріне алаңдамайтын қабілет болуы керек. Ал ол қабілет тәжірибеге сүйенген ұзақ тарихи дамудың нәтижесі. Натурал сандардың N жиыны сан ұғымын кеңейту процесіндегі бастапқы жиын болып табылады. Өте ерте заманда пайда болған натурал сан ұғымы көптеген ғасырлар бойы жалпыланып, кеңейе түсті. Сонда сан жайындағы түсініктер адамзаттың практикалық мұқтаждығына, мәселен шамаларды өлшеу қажеттігіне және математиканың өзінің ішкі мұқтаждығына байланысты кеңейіп отырғандығы байқалады. Мысалы, шамаларды неғұрлым дәлірек өлшеудің мұқтаждығы оң бөлшек ұғым тууына себеп болса, теңдеулерді шешу тәжірибелерімен осы саладағы теориялық зерттеуге байланысты теріс сандар ұғымы пайда болды. Бастапқыда сандардың жоқ екендігін белгілеу үшін қолданылатын нөл теріс сандар енгізілгеннен кейін Z бүтін сандар жиынындағы, сондай-ақ Q рационал сандар жиынындағы толыққанды сан ретінде қарастырылатын болды.

Б. э. д. V ғасырда Пифагор мектебінде кесінді ұзындығын дәл өлшеу үшін оң рационал сандардың жеткіліксіз болатындығы тағайындалды. Кейінірек осы мәселенің шешілуіне байланысты иррационал сандар пайда болды. Ал XVI ғасырда ондық бөлшек енгізілуіне байланысты нақты сандарға қарай қадам жасалды. Нақты сандардың қатаң түрдегі анықталуымен нақты сандар жиынының қасиеті XIX ғасырда тұжырымдалды. Нақты сан ұғымы сандар қатарындағы ең соңғы ұғым емес. Сан ұғымын кеңейту процесін одан әрі жалғастыра беруге болады және бұл процесс жалғасады. Мұны математиканың және басқа да ғылымдардың дамуы талап етуде. Сан жайындағы жаңа түсініктердің пайда болуымен бірге осы жаңа сандық объектілерге амалдар қолдану ережелері қолға алынып отырды, алайда сандар және оларға қолданылатын амалдар туралы жинақталған математикалық теория ретінде XIX ғасырдың II жартысында көптеген көрнекті математиктер математиканың негізгі мәселесімен айналыса бастағанда ғана бір жүйеге келтірілді. Қазірге кезде әртүрлі сан жиындарын мына ретпен қарастыру қабылданған.

1. Натурал сандар (N жиыны)

2. Бүтін сандар (Z жиыны)

3. Рационал сандар (Q жиыны)

4. Нақты сандар (R жиыны)

5. Комплекс сандар (C жиыны)

Мектептің математика курсында сан ұғымын кеңейту оның тарихи дамуына сәйкес қарастырылады.

Жазықтық. Жазықтықтың әртүрлі берілу тәсілдері

Жазықтық – геометрияның негізгі ұғымдарының бірі. Геометрияның жүйелі курсын тұжырымдағанда жазықтық ұғымы бастапқы ұғым ретінде алынады, ал оның жанама анықтамасы геометрия аксиомаларында беріледі. Жазықтықтың кейбір сипаттамалық қасиеттері мынадай:

1. егер түзудің екі нүктесі жазықтықта жатса, онда түзудің барлық нүктелері сол жазықтықта жатады;

2. жазықтық – берілген екі нүктеден бірдей қашықтықтағы нүктелердің жиыны. 

Жазықтық – бірінші реттік алгебралық бет. Ол декарттық координаттар жүйесінде 1-дәрежелі теңдеумен берілуі мүмкін. Жазықтықтың жалпы (толық) теңдеуі былай өрнектеледі: Ax+By+Cz+D=0, мұндағы A, B, C, D – тұрақтылар.

Жазықтықтың теңдеуі алғаш рет 1731 жылы француз математигі Алекси Клеронның (1713 - 1765) еңбектерінде кездескен.

Жанасу жазықтығы - беттің берілген нүктесі арқылы өтетін жазықтық.

Комплекстік жазықтық - комплекс сандарды геометриялық тұрғыда бейнелеуге арналған тікбұрышты декарттық координаттық жүйе және де абсцисса осінің бойына нақты сандар, ал ордината осі бойына - жорамал сандардың коэффиценттері салынатын жазықтық.

Координаттық жазықтық - координаттық екі осін қамтитын жазықтық.

Қима жазықтық - берілген денеге немесе жазықтыққа тиісті болатын бос (құр) емес жиын.

Қиюшы жазықтық - берілген дене мен қима жазықтық үшін ортақ болатын нүктелер жиыны.

Аксиомалық әдіс немесе Формалды теория — ғылыми теорияны аксиомалар деп аталатын негізгі тұжырымдар арқылы құру тәсілі. Аксиомалық әдісті пайдаланудың үлгісін Евклид (біздің заманымыздан бұрын III ғасырда) өзінің атақты “Негіздер” деп аталатын еңбегінде көрсетті. XIX ғасырдың басында орыс ғалымы Н.И.Лобачевскиймен венгр математигі Я.Больяйдің (1802—60 жылдары) ашқан Евклидтік емес геометриясы аксиомалық әдістің одан әрі дамуына үлкен әсер етті. Олар Евклидтіңпараллельділік туралы 5-қағидасын теріске шығара отырып, таза логикалық әдіс арқылы Евклид геометриясы сияқты үйлесімді әрі мазмұнға бай жаңа геометриялық теория құруға болатындығын дәлелдеді. Бұдан кейін математикадағы аксиомалар жүйесінің қайшылықсыздығы, толықтығы және тәуелсіздігі сияқты жалпы мәселелерді зерттеу күн тәртібіне қойылды. Аксиомалық әдістің одан әрі дамуы неміс математигі Д.Гильберттің (1862—1943 жылдары) еңбектерінде ерекше орын алды. Оның ғылыми бағытында аксиомалық теорияның ұғымы, яғни формальды жүйе ұғымы нақтыланды. Мұның нәтижесінде математикалық теория дәл математикалық объектілер ретінде қарастырылып, жалпы теорияны (метатеорияны) құруға мүмкіндік жасалды. Бұл салада австрия математигі К.Гёдель (1906—78) және американ математигі П.Дж.Коэн (1934) үлкен үлес қосты. Аксиомалық тәсіл — ғылыми теорияларды дедуктивті түрде құру тәсілдерінің бірі. Мұнда:

1. белгілі бір теорияның дәлелдеусіз қабылданатын сөйлемдерінің (аксиомаларының) кейбір жиыны іріктеліп алынады;

2. бұларға енетін түсініктер осы теория шеңберінде айқын түрде анықталмайды;

3. теорияға жаңа сөз атауларын (ұғымдар) енгізуге және бірқатар сөйлемдерді басқаларынан логикалық жолмен шығарып алуға мүмкіндік беретін осы теорияның анықтама ережелері мен түйіндеп шығару ережелері белгіленеді;

4. осы теорияның барлық баска сөйлемдері (теоремалары) жоғарыда айтылғандардың негізінде бірден қорытып шығарылады.

Аксиомалық тәсіл жайындағы "алғашқы көріністер Ежелгі Грекияда (Олеатгар, Платон, Аристотель, Эвклид) пайда болды

Натурал сандар деп мына сандарды атаймыз 0, 1, 2, 3, 4,… Барлық натурал сандар жиының N символымен белгіленеді. Белгілі бір a санының натурал сан екенің көрсету үшін a ∈ N деп белгілейміз. Мысалы 1 ∈ N, 5 ∈ N, 3 ∈ N. [10.06, 11:11] Альбина: Натурал қатар– өсу ретімен орналасқан барлық натурал сандар жиыны N={1, 2, …}. Натурал қатар шексіз және толық реттелген жиын. Әдетте Натурал қатардың кез келген бүтін оң санын натурал сан деп атайды. 

2.Цилиндр. Цилиндр перпендикулчрлық қимасындағы сызықтың түріне қарай төрт түрге бөлінеді: дөңгелек, эллипстік, гиперболалық, және парболалық цилиндр болып, осыған сәйкес цилиндр тік бұрышты координаталар жүйесінде төрт түрлі теңдеумен анықталады: Бұл төрт теңдеу жазықтықта шеңберді, эллипсті, гиперболаны және паболаны кескіндейді, ал кеңістікте дөңгелек, эллипстік, гиперболалық және параболалық цилиндрлейді кескіндейді. Сонымен цилиндр (цилиндрлік бет) дегеніміз шеңбер, элллипс, гипербола, параболалардың бойымен олардың жазықтықтарына перпендикуляр болып өтетін түзу сызықтардың үздіксіз қозғалысынан шығатын екінші ретті беттер.  Осы шеңбер, эллипс, гипербола, және парабола цилиндрлердің бағыттаушылары, ал цилиндрдің беттерінде жатқан түзулер олардың жасаушылары деп аталады. 3.Конус. Конус деп берілген нүктеден өтетін және бағыттаушы қисықтың бойымен жылжитын жасаушы түзудің үздіксіз қозғалысынан шығатын бетті айтады. Конустың бағыттаушысы   эллипс, ал жасаушы түзуі координаталардың бас нүктесінен өтсін. Сонда конустың теңдеуі:  болады.Мұндағы z=c конусты XOY жазықтығына параллель қиып өтетін жазықтық. Ал егер a=b болса, онда конустың перпендикулярлық қимасы шеңбер болады:  - айнымалы концстың теңдеуі.  Егер a=b=c болса, онда мынандай конус шығады: Төбесі координаталардың бас нүктесінде апликата осіне симметриялы екінші ретті конустық беттің теңдеуі. Дәл осындай қалған екі оське симметриялы конустық беттің теңдеулері мынандай болады:

БҮТІН САН — натурал сандардың айырымы түрінде өрнектеуге болатын сан. Натурал сан, теріс натурал сан, немесе нөл бүтін сан болып есептеледі. Барлық бүтін сандар жиыны 2 болып белгіленген (бұл немісше "zahl — сан" деген сөзінің алғашқы әрпі.

Бүтін сандар қосындысы, алындысы және көбейтуі бүтін сан болады. Бүтін сандардың бөлуі әрқашан бүтін сан болмайды. Мысалы, (-5):2=-2,5 Z. Сан түзуінде бейнеленген бүтін сандар, бүтін сандардың торын құрайды. Басқаша айтқанда , әрбір n бүтін саны үшін алдында n 1, одан кейін n 1 жалғыз саны келеді. Ал бүтін сан емес кез келген p саны көршілес бүтін сандардың арасында орналасады : n  p  n 1, қайда n  Z . Сонда n саны , ( p санын аспайтын, ең үлкен бүтін сан ) p санының бүтін бөлімі деп аталады және [ p] деп белгіленеді. n бүтін санының бүтін бөлімі n саны болып келеді.

Рационал Сан^[1]– түріндегі сан, мұндағы m және n — бүтін сандар (n-0). m бүтін санын түрінде жазуға болатындықтан, барлық бүтін сандар Рационал Сан болып есептеледі. Рационал Сандар алгебр. өріс құрайды, өйткені Рационал Сандарға қосу, азайту, көбейту және бөлу (нөлден басқа бөлгішке) амалдарын қолданғанда Рационал Сан шығады.

Рационал Санды ондық бөлшек немесе шекті және шексіз периодты ондық бөлшек түрінде жазуға болады.

Декарттық координаттар жүйесі немесе картезиандық координаттар жүйесі - координаттар осіндегі межелері немесе базистік векторларының ұзындықтары тең, жазықтықтағы немесе кеңістіктегі түзу сызықты координаттар жүйесі. Әдетте, тікбұрышты декарттық координаттар жүйесі қолданылады. Бұл жүйені 1637 жылы француз ғалымы Рене Декарт (1596 - 1650) енгізген. Нақты сандарды көрнекі түрде өрнектеу үшін сан түзуі пайдаланады. Әрбір нақты санға сан түзуінің бір нүктесі сәйкес болады және керісінше - сан түзуінің әрбір нүктесіне бір нақты сан сәйкес болады. Өзара перпендикуляр екі сан түзуі тікбұрышты(декарттық) координаттар жүйесін түзеді.Сан түзулері координаттар осьтері деп аталған.Осылардың қиылысу нүктесіне екі сан осінің бас нүктесі 0(нөл) саны сәйкес болады.Осы коорлинаттар жүйесі жазықтықты төрт бөлікке – квадрттарға бөледі. Декарт координаттары - жазықтықта белгіленген өзара перпендикуляр екі түзуге (өстерге) дейінгі қашықтықтары арқылы нүктенің жазықтықтағы орнын анықтау әдісі. 

Кез келген үш нүктенің коллинеарлық шарты сақталып, бір мәнді кеңістіктің нүкетлік түрленуі аффиндық түрлендіру деп аталады. Бұл түрлендіруде үш коллинеарлық нүкте үш коллинеарлық нүктелерге көшеді.

Аффиндық түрлендірудің негізгі қасиеті мынау: кеңістіктің кезе келген аффиндық түрленуі сызықтық түрленуге жатады. Аффиндық түрлендірудің қасиеттері мынадай:

1. өз ара коллинеар болмайтын кеңістіктің үш нүктесі коллинеар емес үш нүктеге,

2. өз ара компланар болмайтын төрт нүкте компланар емес төрт нүктеге,

3. түзу сызық түзу сызыққа,

4. қиылысатын екі түзу қиылысатын екі түзуге

5. бір параллелограмның төрт төбесі екінші параллелограмның төрт төбесіне,

6. бір кесіндінің ортасы екінші кесіндінің ортасына

7. кеңістіктегі кез келген бір М нүктесі екінші бір М ^’ нүктесінде көшеді. Бұл екі нүктенің әрқайсысы өзіне сәйкес координаталар системасында анықталады.

Егер осы айтылған қасиеттер сақталса, онда мұндай ұғымды аффиндік түрлендіру дейміз. Басқаша айтқанда, еркінше алынған аффиндік түрлендіруде сақталатын геометриялық бейнелердің қасиеттерін аффиндік түрлендіру дейміз. Мысалы, параллелограм, түзу сызық, эллипс, гипербола, парабола аффиндік ұғымға жатады. ал тік бұрышты төртбұрышты, шеңбер аффиндік ұғымға жатпайды. Өйткені аффиндік түрленуде тік бұрышты төртбұрыш параллелограмға ал шеңбер эллипске айналады. Сондықтан бұл екі пішін аффиндік ұғым болмайды. Сонымен түрлендірілгеннен кейін теореманың қасиеті сақталса, онда мұндай теорема аффиндік деп аталады. Мысалы, үш медиана бір нүктеде қиылысады деген теорема аффиндік болады, ал үш биссектриса бір нүктеде қиылысады деген теорема аффиндік теоремаға жатпайды. Аффиндік ұғымдар мен теоремалардың жиындысын аффиндік геометрия деуге болады. Аффиндік геометрияда кесіндінің ұзындығы деген ұғым жоқ. Мұнда кез келген кесіндіні координаталық вектор деп қабылдауға болады. Аффиндік түрленудегі координаталық вектор ұзындығы еркінше алынатын кез келген вектор болуы мүмкін. Осы сияқты аффиндік геометрияда аудан мен көлем де анықталмайды.

у

М

r₁

r₂

F₁ O F₂

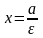
F₁, F₂ – эллипстің фокустары. F₁ = (-c; 0); F₂(c; 0), F₁F₂ = 2c.

с – фокустары ар қашықтығының жартысы; 2а - тұрақты шама. F₁М және F₂М қашықтықтарын r₁= F₁М, r₂= F₂М деп белгілесек, онда (2) теңдік мына түрде жазылады:

r₁ + r₂ = 2а (2¹)

Екі нүктені ара қашықтығының формуласы бойынша:

.

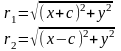
Бұл теңдеуді түрлендіріп, эллипстің жабайы (канондық) теңдеуін табайық:

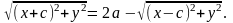
х ²+2сх+с²+ у² = 4а² – 4а

а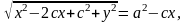 теңдіктің екі жағын а - ға бөліп, квадраттайық:

х² -2сх+с²+у² = (а -

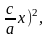
х² -2сх+с²+у² =

а²х²+а²у²+а²с²= а⁴ + с²х²,

(а²- с²) х²+а²у²+ = а² ( а² - с²),

а с болғандықтан, а² - с² 0 болады, сондықтан а² - с² в² (3) деп белгілейміз.

Сонда в² х²+а²у²+ = а² в² шығады, осыдан (4), мұндағы х пен у -

эллипстің бойындағы кез келген нүктелердің координаталары, а – эллипстің үлкен жарты өсі, в – оның кіші жарты өсі. (4) теңдеу эллипстің жабайы (канондық) теңдеуі деп аталады.

Теорема. Эллипстің фокустық ара қашықтығы мен жарты өстері мынадай қатынас бойынша байланысады:

a² = b² + c².

Дэлелдеу: Егер М нүкте эллипстің вертикаль осьпен қиылысу нүктесінде болса, онда r₁ + r₂ = 2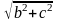 ( Пифагор теоремасы бойынша). Егер М нүкте эллипстің горизонталь осьпен қиылысу нүктесінде болса, онда r₁ + r₂ = a – c + a + c. Эллипстің

нықтамасы бойынша r₁ + r₂ – қосынды тұрақты шама, ендеше жоғарыдағы екі теңдікті теңестіріп, мынадай теңдік аламыз:

a² = b² + c² .

Анықтама. 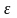= с/a қатынас эллипстің эксцентриситеті деп аталады. с < a

болғандықтан, < 1 болады.