Оценка параметров распределения выборки

Первую группу составляют методы оценивания параметров по конечной выборке, вторую — методы оценивания по неограниченно растущей выборке. В качестве характеристик распределения часто используют моменты (метод моментов), реже — квантили (метод квантилей). Вместо словосочетания «приближенное значение» в статистике используется термин «оценка» переопределении параметров распределении.

В соответствии с теоремой больших чисел оценка математического ожидания а является среднее арифметическое значение .

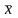Для дисперсии генеральной совокупности Dтакой оценкой для выборки является s² , которая определяется по формуле

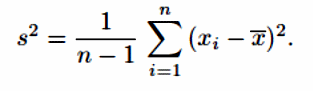⁽⁴⁾

где, n – число элементов выборки.

Для сравнения двух выборок полученных с разными атрибутами социального статуса необходимо дать оценку области, в которой этот параметр находится с вероятностью, не менее, заданной вероятностью 95-99%. В одномерном случае доверительную область называют доверительным интервалом. С уровнем доверия для неизвестного нам истинного значения[1].

Если удалось доказать, что распределение соответствует нормальному закону распределения или, если принять такую гипотезу, то оценку неизвестного a (математического ожидания), если считать дисперсию известной, можно дать с помощью неравенства

(5)

где, z_1- это квантиль стандартного нормального закона распределения, соответствующее вероятности 1-2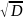.  это среднеквадратическое отклонение выборки.

Эта оценка задаёт интервал

(6)

с центром . Этот интервал называется доверительным интервалом для неизвестного а, с коэффициентом доверия 1-2

Если считать дисперсию неизвестной, то для оценки математического ожидания следует использовать распределение Стьюдента. В этом случае значение параметра a находится в интервале с коэффициентом доверия 1-2

. (7)

Доверительный интервал для дисперсии имеет вид

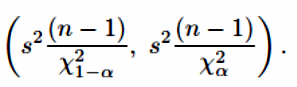, (8)

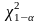где и 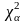квантили распределения соответствующие коэффициенту доверия 1-2

Возможно, что влияние атрибута на математическое ожидание не значимо, а на дисперсию, характеризующую разброс значений относительно средний.

Для оценки влияния атрибута на разброс значения успеваемости следует оценить дисперсию.

Сравнение оценок двух выборок

Для оценки параметров выборок будем использовать гипотезу о нормальном законе распределения успеваемости. Если оценки дисперсии двух выборок имеет перекрывающийся доверительный интервал, будем считать, что дисперсии равны __. Будем полагать в соответствии, что математически ожидания не отличаются от двух рассматриваемых выборок на уровне значимости , если

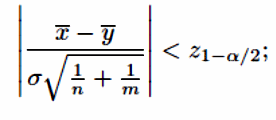
(9) в противном случае гипотеза отвергается в пользу альтернативы a₁ ≠ a₂.

Если оценки дисперсии двух выборок имеют не перекрывающиеся интервалы, то полагаем, что дисперсии известны, но не равны между собой. В этом случае гипотеза о равенстве математических ожиданий принимается

| | < .

(10)

Получив оценки нескольких выборок, имеющих разные атрибуты социального статуса можно судить о наличии или отсутствии статистически значимого влияния атрибутов. Если доверительные интервалы для сравниваемых выборок перекрываются, то влияние (в смысле смещения среднего) пренебрежимо мало с коэффициентом доверия 1-2