1.Principy bilancování. Bilancovatelné veličiny. Pojmy: bilanční systém a jeho hranice, bilanční období, proud, složka, akumulace, zdroj, fiktivní proud, základ bilance. Sestavování bilančních vztahů, celková bilance, bilance složky, počet nezávislých bilančních vztahů. Dodatečné vztahy k bilančním rovnicím: konverze, výtěžek, přebytek složky. Matice zadání a výsledků, doporučený postup při bilancování.

Bilancované veličiny

• Bilancujeme extenzivní veličiny (celková hmotnost, hmotnost složky, celkové látkové množství, látkové množství složky, hybnost, energii, entalpii)

• Intenzivní veličiny bilancovat nelze (teplota)

Bilanční systém

• Část prostoru vymezená od okolí skutečným nebo myšleným rozhraním (hranicí)

• Část prostoru, ve kterém se odehrává sledovaný proces (jedno zařízení, soustava zařízení)

Hranice systému

• Reálné (stěny zařízení) x Pomyslné

• Nepohyblivé (stěny zařízení) x Pohyblivé (povrch tekoucí kapky)

Typy Systémů :

Otevřený systém

• Vyměňuje hmotu i energii s okolím, hranice systému jsou propustné

• Bilancované veličiny vstupují do systému vstupními proudy a vystupují proudy výstupními

Uzavřený systém

• Systém nevyměňuje s okolím hmotu

Izolovaný systém

• Systém s okolím nevyměňuje ani hmotu ani energii

Strukturu systému

• vyjadřujeme pomocí blokového (proudového) schématu – to vystihuje strukturu systému,

• uzly představují jednotlivá zařízení nebo skupiny zařízení, jednotlivé uzly jsou propojeny proudy (pomocí proudů jsou popsány všechny nezanedbatelné interakce uzlu s okolím nebo jinými uzly)

• Reálné proudy – jednotlivé materiály vstupují do nebo vystupující ze systému

• Fiktivní proudy – používají se při probíhající chemické reakci v uzlu, výstupní fiktivní proud vyjadřuje zánik některých složek (reaktantů), vstupní fikt. proud vznik jiných složek (produktů reakce)

(Bilancovaná veličina se může před začátkem bilance vyskytovat v bilancovaném zařízení nebo její část v zařízení zůstane na konci bilance, počáteční množství veličiny lze také nahradit fiktivním proudem vstupujícím, konečné zůstatkové množství veličiny lze nahradit fiktivním proudem vystupujícím)

• Proudy se značí arabskými číslicemi, uzly se značí číslicemi římskými

Bilanční období

• je vymezeno dvěma časovými údaji, definují začátek a konec bilančního období (za rok, měsíc, minutu) – „konečné bilanční období“

• Velmi krátké (intenzivně malé) období dt následující za definovaným časem t – všechny členy bilanční rovnice jsou pak velmi malé, vydělíme-li všechny tyto členy touto malou délkou bilančního období, získáme členy vztažené na jednotku času, lokalizované v čase – „diferenciální bilanční období“

• Bilance za konečné bilanční období

Počáteční množství + součet vstupů + součet zdrojů = konečné množství + součet výstupů

Vstup + zdroj = výstup + akumulace

• Počáteční množství – množství bilancované veličiny, které se nachází v bilančním systému v okamžiku začátku bilančního období

• Konečné množství - množství bilancované veličiny na konci bilančního období

• Akumulace (přírůstek) – množství bilancované veličiny, které v bilančním systému v průběhu bilančního období přibude, (tj. rozdíl, který získáme tak, že od množství bilancované veličiny v bilančním systému v okamžiku konce bilančního období odečteme množství bilancované veličiny v bilančním systému v okamžiku začátku bilančního období, může mít kladnou, nulovou (ustálený, stacionární stav) nebo zápornou hodnotu (úbytek))

Akumulace = konečné množství – počáteční množství

• Vstup – množství bilancované veličiny , které se v průběhu bilančního období přemístí z okolí bilančního systému přes hranice systému do systému

• Výstup – množství veličiny, které se během bilančního období přemístí ze systému do okolí systému

• Zdroj – množství veličiny, které v bilančním systému během bilančního období vznikne nebo zanikne (např. hmotnost nějaké sloučeniny může vznikat chemickými reakcemi za současného zániku jiné sloučeniny)

• Bilance za diferenciální bilanční období

Vstup za jednotku času + zdroj za jednotku času = výstup za jednotku času + akumulace za jednotku času

Přítok + rychlost vzniku = odtok + rychlost akumulace

Materiálové bilance

• Bilancujeme hmotnost, nebo látkové množství

• Složky jsou látky, které bilancujeme

• S chemickou reakcí

  • Rozsah reakce – kvantitativní charakteristika, která nám říká, do jaké míry reakce proběhla 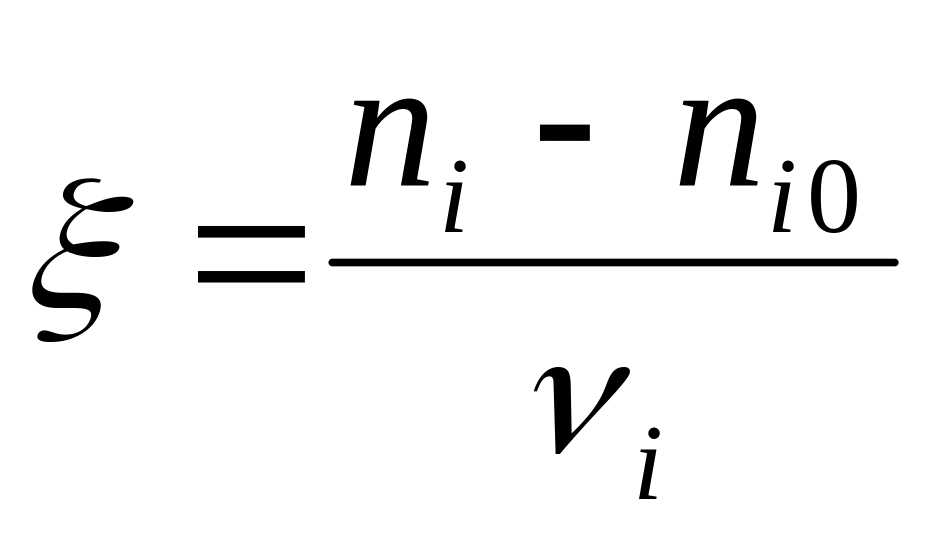n₀ – počáteční, n_i – konečné látkové množství

  • Konverze i-té složky – množství složky, které skutečné zreagovalo, vydělené celkovým počátečním nebo vstupním množstvím složky

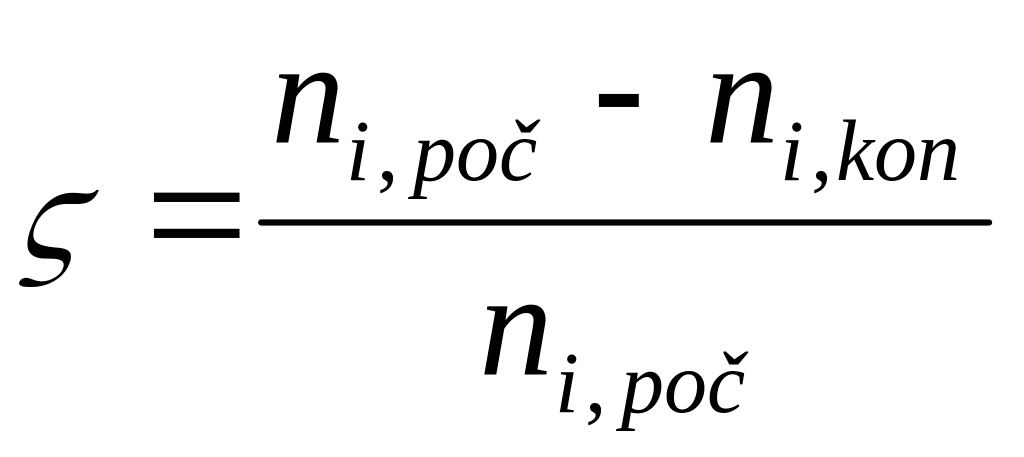
  • Přebytek i-té složky vzhledem k jiné složce či složkám

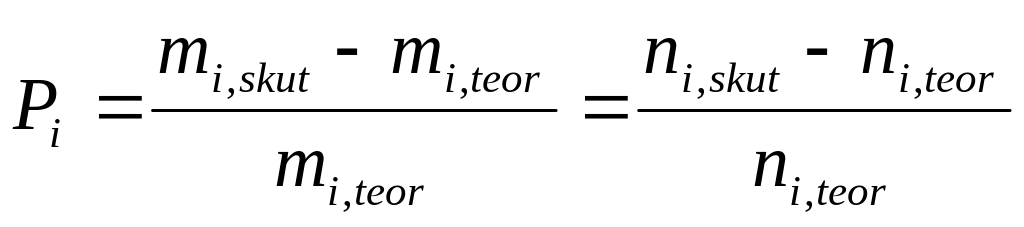
Postup při řešení materiálových bilancích

• Nakreslíme bilanční schéma a označíme uzly a proudy

• Probíhají-li v procesu chemické reakce, zapíšeme všechny stechiometrické rovnice a doplníme bilanční schéma o dvojice fiktivních proudů za každou uvažovanou reakci

• Definujeme všechny složky, které se v procesu vyskytují

• Rozhodneme, zda budeme bilancovat hmotnost nebo látkové množství

• Přepočítáme údaje ze zadání na veličiny, ve kterých budeme bilancovat, vyčíslíme složeních fiktivních proudů pro chemické reakce

• Všechny údaje sepíšeme do tabulky zadání, neznámé označíme příslušnými symboly

• Z matice spočítáme počet neznámých a zjistíme zda máme k dispozici stejný počet použitelných rovnic (bilanční rovnice + dodatečné vztahy – součet molárních či hmotnostních zlomků = 1, definice přebytku či konverze, hmotnost fiktivnich proudů je stejna látkové množství ne )

• Řešíme systém rovnic

• Formulujeme odpovědi

2.Tekutiny, spojité prostředí (kontinuum). Síly působící v tekutinách, tečné a normálové napětí, tlak. Newtonův zákon pro viskozitu. Ideální tekutina. Laminární a turbulentní proudění, Reynoldsovo kritérium. Rychlostní profil při proudění tekutiny trubkou. Rovnice kontinuity.

Tekutiny – plyny, páry, kapaliny

• plyny a páry mají mnohem větší vzdálenosti mezi molekulami, proto jsou více stlačitelné než kapaliny (pracujeme s útvary, jejichž délkové rozměry jsou mnohem větší než je střední mezimolekulární vzdálenost – plyny 10^-8 m, kapaliny 10^-10 m)

• Vzduch - elementární objem dV=10^-9 mm³

- 3x10⁷ molekul

• Izotropní prostředí – fyzikální vlastnosti nezávisejí na směru ve kterém jsou měřeny

Síly

• Objemové (hmotnostní) – působí na tekutinu zvnějšku a jejich velikost je úměrná objemu (hmotnosti) tekutiny, na kterou působí – gravitační, odstředivá, magnetická, elektrostatická

• Plošné – působí v tekutinách na plochy, ať jsou již skutečné nebo smyšlené ( např. rozhraní mezi dvěma nemísitelnými tekutinami, rozhraní mezi tekutinou a pevnou fází, nebo myšlené rozhraní mezi dvěma vrstvami kapaliny pohybující se různou rychlostí)

– plocha představuje vektorovou veličinu, má velikost a směr, směr plochy dA je dán jejím normálovým vektorem (kolmicí, normálou) je vektor kolmý k dané ploše jehož absolutní velikost je rovna velikosti plochy, síla působící na plochu může mít jakýkoli směr, rozkládá se na tři směry, na směr rovnoběžný se směrem normály plochy „normálový směr“ a do dvou směrů k normále kolmých - tečné ( ), působí-li síla normálová ve směru opačném vůči směru normály, označuje se jako síla tlaková a po vydělení této síly velikostí plochy dostáváme tlak, smykové síly vyjádřené na jednotku plochy se označují jako tečné (smykové) napětí

Hydrostatika

• Jestliže jsou tekutiny v klidu, neexistují v nich smykové síly

• Napětí v tekutině v klidu je vždy kolmé na libovolnou plochu uvnitř tekutiny

• Kolmá síla na jednotku plochy = tlak

• V každém místě tekutiny je tlakové napětí stejné ve všech směrech, tlak se od místa k místu může měnit

Proudění tekutin

• Rychlostní profil – vytvoří se při proudění tekutiny podél nehybné pevné stěny; pokud je pevná látka pro tekutinu nepropustná, je rychlost proudění ve směru kolmém k povrchu nulová, v naprosté většině případů je také tečná rychlost při povrchu pevné látky nulová (těsně u stěny má tekutina nulovou rychlost) a směrem od stěny se rychlost zvětšuje – důsledek existence smykových sil (viskozity)

• Dynamická Viskozita (konstanta úměrnosti) [Pa.s] tekutin závisí na teplotě, pro plyny s rostoucí teplotou roste a pro kapaliny většinou klesá

• Newtonův zákon pro viskozitu