Міністерство освіти і науки україни Національний університет «Львівська політехніка»

Елементи теорії похибок завдання та методичні рекомендації

до лабораторної роботи № 1 з курсу

«Чисельні методи»

для базового напрямку 040204 «Прикладна фізика»

Затверджено

на засіданні кафедри

обчислювальної математики та програмування

Протокол № 5 від 30.01.2012 p.

ЛЬВІВ – 2011

ЕЛЕМЕНТИ ТЕОРІЇ ПОХИБОК. Завдання та методичні рекомендації до лабораторної роботи № 1 з курсу «Чисельні методи» для базового напрямку 040204 «Прикладна фізика» / Укл. Я.М.Глинський, Н.М.Гоблик, З.О.Гошко, В.А.Ряжська, 2012. – 11 с.

Укладачі: Глинський Я.М., канд. фіз.-мат. наук, доц.

Гоблик Н.М., ст. викл.

Гошко З.О., асистент

Ряжська В.А., канд. фіз.-мат. наук, доц.

Відповідальна за випуск Ряжська В.А., канд. фіз.-мат. наук, доц.

Рецензент доктор фіз.-мат. наук, проф. Чабанюк Я.М.

Передмова

У методичних вказівках розглянуто основні види похибок, що виникають під час вимірювання, та методика їх оцінювання; наведено приклади обчислень похибок наближених величин.

Методичні вказівки містять типове короткі теоретичні відомості, приклади розв’язування типових задач, а також індивідуальні завдання для самостійної роботи студентів.

Методичні вказівки призначені для студентів базового напрямку 040204 «Прик­ладна фізика» і укладені відповідно до робочої програми курсу «Чи­сель­ні методи».

1. Мета роботи

Мета роботи – ознайомитись з основними видами похибок, що виникають під час вимірювання, та методикою їх оцінювання; навчитись обчислювати похибки наближених величин.

2. Теоретичні відомості

Класифікація похибок

Під час розв'язування інженерних задач обчислювальні експерименти часто виконують з набли­же­ними даними, застосовують наближені методи і різні обчислювальні пристрої від калькулятора до сучасного комп’ютера. Тому майбутній інженер повинен:

• знати можливі джерела похибок;

• вміти правильно записувати наближені дані й результати;

• вміти оцінювати похибку результату за заданими похибками даних;

• вміти обирати най раціональніший порядок обчислень;

• вміти обирати алгоритм обчислення, найстійкішій до похибок;

• вміти відслідковувати хід і результати обчислень з метою недопущення грубих похибок.

Похибки, що виникають під час розв’язування задачі, можна віднести до трьох груп:

• неусувна похибка;

• похибка методу;

• похибка обчислень.

Неусувна похибка є наслідком

• неточності вхідних даних задачі;

• поганої відповідності математичної моделі реальній задачі.

Похибка методу виникає, коли для розв’язування математичної задачі вико­ристовують не точні, а наближені методи. Різні наближені методи характеризуються різними похибками.

Похибка обчислень виникає на всіх етапах опрацювання вхідних і проміжних даних обчислювальним пристроєм. Різні обчислювальні пристрої характеризуються різною точністю обчислень.

Абсолютна та відносна похибки

Нехай x – точне значення деякої величини, яке досліднику зазвичай невідоме, а а – її відоме наближене значення.

Абсолютною похибкою числа а називають деяку величину , що задовольняє умові

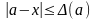
Відносною похибкою числа а називають деяку величину 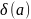, що задовольняє умові

Точність результату краще характеризує відносна похибка. Інформацію про відомі наближене значення і абсолютну та відносну похибки можна використати для наступного подання числа x:

Приклад 1. Визначити абсолютну та відносну похибки операції заокруглення числа 0,7245 до трьох значущих цифр.

Заокруглюючи задане число до трьох значущих цифр, отримаємо наближене число x* = 0,725. Його абсолютна похибка дорівнює 0,0005, а відносна похибка δ дорівнює

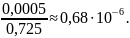
Відносну похибку можна вимірювати у відсотках, наприклад, 0,0068 = 0,68%.

Значущими цифрами числа називаються всі цифри в його запису, починаючи з першої ненульової зліва.

Приклад 2. Розглянемо числа, та визначимо їхні значущі цифри.

x = 7,745634 – всі цифри в запису цього числа значущі;

x = 0,003616 – значущі цифри тільки 3, 6, 1, 6;

x = 0,081600 – значущі цифри 8, 1, 6, 0, 0 (два останні нулі в запису числа є значущими).

Значуща цифра називається вірною, якщо абсолютна похибка числа не перевищує половини одиниці розряду, що відповідає цій цифрі.

Приклад 3. Нехай а = 23,528 і відомо, що 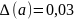. Скільки вірних значущих цифр має число а?

Розв’язання. Маємо 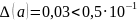. Розряду –1 відповідає остання вірна цифра 5. Отже, у числа a вірними будуть зна­чущі цифри 2, 3, 5, а останні цифри 2 і 8 – сумнівні.

Пряма задача теорії похибок

В деякій області G n-вимірного простору розглядається неперервно-диференційована функція y = f(x₁, x₂,…, x_n). Припустимо, що потрібно обчислити значення цієї функції в точці (x₁, x₂,…, x_n)  G, якщо відомі тільки наближені значення 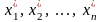та їх похибки.

Абсолютну похибку наближеного значення 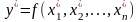можна визначити за формулою

,

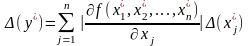Тоді відносну похибку можна обчислити за формулою:

.

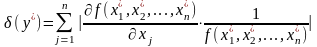Користуючись вищенаведеними формулами, отримаємо формули для обчислення похибок математичних операцій.

Похибка суми.

.

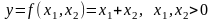Абсолютну похибку у знайдемо за формулою

Оскільки , то

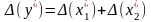
Відносна похибка суми відповідно дорівнюватимемо

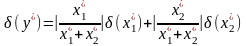
або

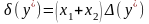
Похибка різниці.

.

,

.

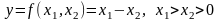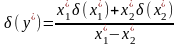Похибка множення.

.

,

.

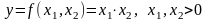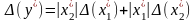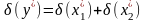Похибка ділення.

.

,

.

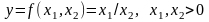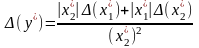Отже, абсолютні похибки суми та різниці дорівнюють сумі абсолютних похибок аргументів, а відносні похибки множення і ділення дорівнюють сумі відносних похибок аргументів.

Зауваження. Якщо віднімаються два близькі числа, то відносна похибка результату може значно зрости і призвести до втрати вірних значущих цифр результату. Під час ділення на досить мале число може значно зрости абсолютна похибка, що також приведе до втрати точності результату.

Обернена задача теорії похибок

Обернена задача теорії похибок полягає в наступному: з якою точністю потрібно задати значення аргументів 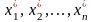деякої функції , щоб похибка значення функції не перевищувала заданої величини.

Для функції однієї змінної y = f(x) абсолютну похибку аргумента можна наближено обчислити за формулою

.

Для функції декількох змінних 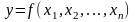задачу розв’язують на основі правила-гіпотези рівних впливів:

а) вважаємо, що всі доданки 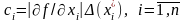рівні між собою. Тоді абсолютні похибки всіх аргументів визначають формулою

;

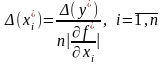б) вважаємо всі похибки рівними, причому максимально можливими, тобто покладемо

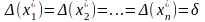, де .

Приклад 4. Сторона квадрату дорівнює 2м. З якою точністю її потрібно виміряти, щоб похиб­ка обчислення площі не перевищувала 1см²?

Позначимо сторону квадрату через x; S = x², S' = 2x. Тоді за формулою визначення абсолютної похибки аргументу отримаємо

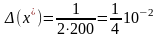см. Отже, похибка вимірювання сторони повинна не перевищувати чверті сантиметра.