Порядок побудови годографа Михайлова.

Для розімкненої системи:

Критерій стійкості Найквиста.

(амплітудно частотний критерій)

Цей критерій дозволяє судити про стійкість замкненої системи автоматичного управління на основі аналізу АФХ розімкненої системи.

В багатьох випадках оцінити стійкість розімкненої системи досить нескладно. Зокрема, якщо розімкнена система складається з послідовних з’єднань стійких ланок і не містить місцевих зворотних зв’язків, то така розімкнена система буде стійкою.

Нехай передаточна функція розімкненої системи має вигляд:

;

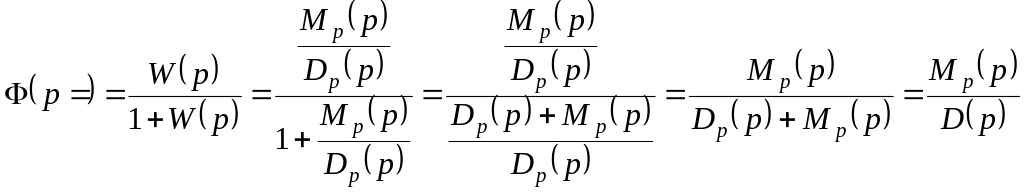
- поліном знаменника передаточної функції розімкненої САУ;

- поліном чисельника розімкненої системи.

- поліном знаменника передаточної функції замкненої системи.

; ; .

Введемо додаткову функцію:

Припустимо, що розімкнена система стійка.

(2)

Нехай характеристичний багаточлен замкненої системи має l правих коренів

(3)

Підставимо (2) і (3) у (1):

Для того, щоб замкнена система була стійка необхідно виконання умови , тобто відсутність правих коренів:

(4)

Умова (4) може бути виконана тільки в тому випадку, якщо функція не охоплює початок координат.

Перший критерій Найквиста:

Якщо розімкнена система є стійкою, то вона буде стійкою і в замкнутому стані при умові, що АФХ системи не охоплює на комплексній площині с координатами .

Розрізняють АФХ першого та АФХ другого роду:

АФХ першого роду – це АФХ, яка дійсну вісь на відрізку не перетинає.

Якщо АФХ перетинає вісь на відрізку , то таку АФХ називають АФХ другого роду.

Перехід характеристики через вважають додатнім, якщо при зростанні частоти характеристика перетинає цю лінію зверху вниз, якщо – з низу в гору, то такий перехід називають від’ємним.

Другий критерій Найквиста:

Якщо розімкнена система стійка і має АФХ другого роду, то вона буде стійкою і в замкненому стані, при умові що різниця між додатними переходами АФХ розімкненої системи через відрізок осі дорівнює 0.

Третій критерій Найквиста:

Якщо розімкнена система є нестійкою і має АФХ другого роду, то вона буде стійкою в замкненому стані, якщо різниця між числом додатних і від’ємних переходів через відрізок дорівнює , де число правих коренів характеристичного рівняння розімкненої САУ.

Якщо АФХ асимптотично наближається до відрізку осі , то вважається, що це перехід, який дорівнює . Якщо АФХ починається на відрізку , то цю точку теж переходом із значенням .

Логарифмічний критерій стійкості.

Є модифікацією критерію Найквиста. Цей критерій дозволяє оцінити стійкість системи в замкненому стані за виглядом ЛАЧХ і ЛФЧХ розімкненої системи.

1 – стійка;

2 – нейтрально стійка;

3 – нестійка.

частота зрізу.

Частота при якій ЛФЧХ перетинає називається .

Перше формулювання:

Стійка розімкнена система буде стійкою і в замкненому стані, якщо її ЛАЧХ перетинає вісь частот раніше ніж ЛФЧХ перетинає лінію .

На всьому діапазоні

Друге формулювання:

Якщо розімкнена система є стійкою, а її ЛФЧХ перетинає лінію при , то вона буде стійкою у замкненому стані, якщо різниця додатних і від’ємних переходів дорівнює 0. При чому перетин ЛФЧХ лінії з низу вгору вважають додатним, а з гори вниз – від’ємним.

Запаси стійкості.

Система стійка.

запас стійкості по амплітуді.

В деяких випадках за виглядом АФХ досить складно визначити запаси стійкості. Для цього необхідно побудувати зону стійкості.

Вважається що система має необхідні запаси стійкості, якщо АФХ не перетинає зону С.

Вплив параметрів ланки запізнення на стійкість САУ.

Дослідження стійкості за допомогою побудови зон стійкості.

При розробці САУ важливо урахування впливів деяких параметрів.

Для досягнення цієї мети можна користуватися розглянутими вище критеріями стійкості. Але це не завжди зручно і при зростанні порядку характеристичного рівняння розрахункові процедури ускладнюються. Прикладом зручного розв’язку може бути побудова гіперболи Вишнеградського.

Для САУ характеристичне рівняння яких має третій порядок.

(1)

(2)

Приведемо рівняння до трьох коефіцієнтів:

(3)

; ;

(4)

; (7)

(8)