БІЛЕТ № 1
Частотні характеристики типових динамічних ланок.
Типові динамічні ланки.
Типовою ланкою називається елемент або система, яка має характерний перехідний процес, та відповідну передаточну, частотну функцію.
До основних типових ланок відносяться:
- підсилювальна ланка;
- ідеальна інтегруюча ланка;
- аперіодична ланка;
- коливальна ланка;
- ідеальна диференціюча ланка;
- диференціюча ланка першого порядку;
- диференціюча ланка другого порядку;
- ланка запізнення.
1) Підсилювальна ланка
Називається ланка, рівняння якої має вигляд:
Передаточна функція:
В літературі підсилювальна ланка зустрічається як безінерційна ланка.
ЛАЧХ та ЛФЧХ
2) Ідеальна інтегруюча ланка.
Передаточна функція:
АЧХ
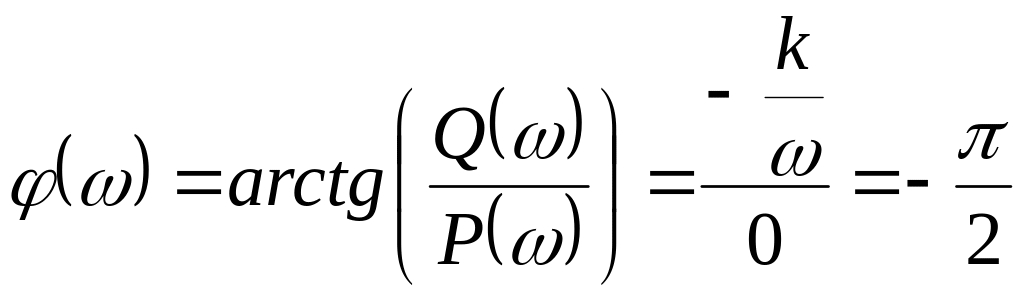
ФЧХ АФХ
ЛАЧХ
;
;
Типові нахилиш
3) Ідеальна диференціюча ланка.
Передаточна функція:
при
4) Аперіодична ланка
Т – постійна часу;
k – коефіцієнт підсилення.
k
є коефіцієнт
пропорціональності між вхідною величиною
та усталеним значенням вихідної величини
і дорівнює передаточній функції при
ЛЧХ
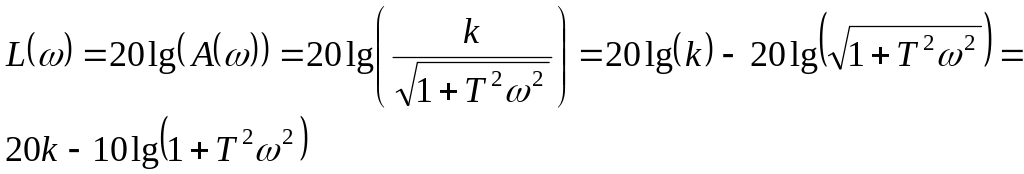
при
Побудову ЛАЧХ будемо здійснювати для двох часових частот
Визначити похибку
ЛФЧХ
с
частота
співпряження.
5) Диференціюча ланка.
Передаточна функція:
Приклад:
6) Коливальна ланка.
k – коефіцієнт підсилення;
Т – постійна часу;
коефіцієнт
демпферуваня.
Рівняння динаміки коливальної ланки часто представляють в такій формі:
де
;
;
.
В
залежності від
коливальна ланка може бути:
- Чисто коливальною ланкою;
- Консервативною ланкою;
- аперіодичною ланкою другого порядку.
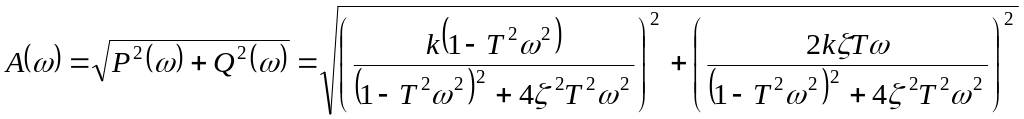
ЛФЧХ
ЛАЧХ
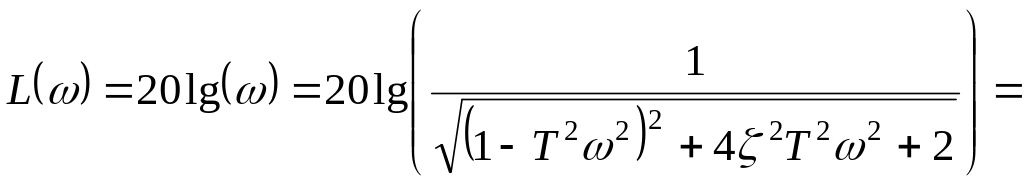
7) Диференціюча ланка другого порядку.
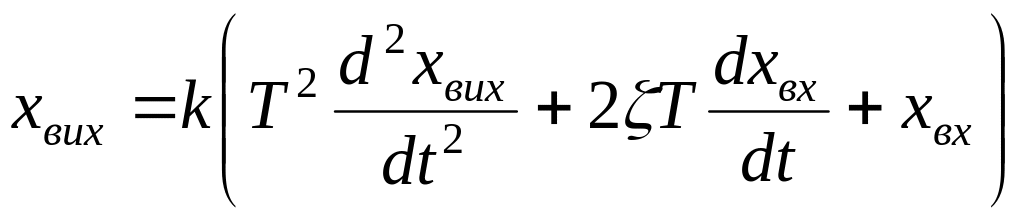
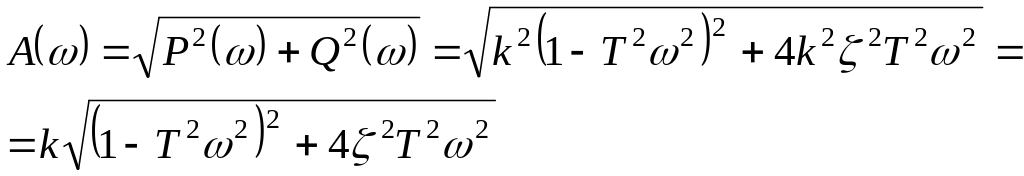
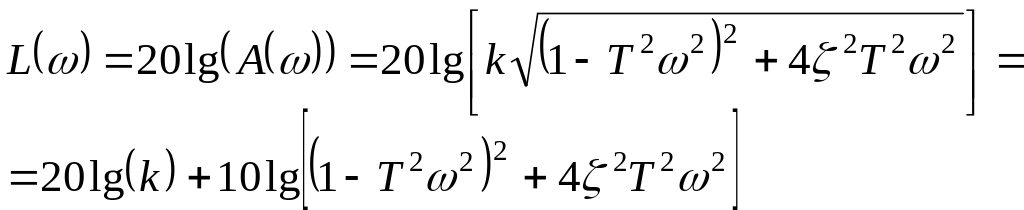
8) Ланка з запізненням.
час
запізнення.
ЛАЧХ
Приклад:
Визначити
параметри і частотні характеристики
(
,
,
,
,
,
ЛАЧХ, ЛФЧХ):
1)
БІЛЕТ № 2
ЛАЧХ і ЛФЧХ типових динамічних ланок.
Типові динамічні ланки.
Типовою ланкою називається елемент або система, яка має характерний перехідний процес, та відповідну передаточну, частотну функцію.
До основних типових ланок відносяться:
- підсилювальна ланка;
- ідеальна інтегруюча ланка;
- аперіодична ланка;
- коливальна ланка;
- ідеальна диференціюча ланка;
- диференціюча ланка першого порядку;
- диференціюча ланка другого порядку;
- ланка запізнення.
1) Підсилювальна ланка
Називається ланка, рівняння якої має вигляд:
Передаточна функція:
В літературі підсилювальна ланка зустрічається як безінерційна ланка.
ЛАЧХ та ЛФЧХ
2) Ідеальна інтегруюча ланка.
Передаточна функція:
АЧХ
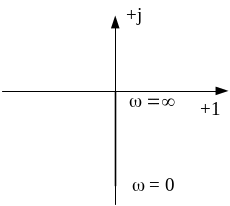
ФЧХ АФХ
ЛАЧХ
;
;