1.7. Різниця потенціалів

Для внесеного пробного заряду отримаємо

(1. 14)

де φ – потенціал електричного поля в точці а, В .

Якщо відомо потенціал двох точок поля, то різниця потенціалів, або напруга між ними буде

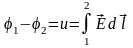, (1.15)

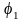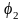де і – потенціали довільних точок поля, відповідно,1 і 2, В; и – електрична напруга , В.

_Або

, (1.16)

де U₁₂ – електрична напруга між точками 1 і 2, В; Е₁ і Е₂ – напруженості електричного поля, відповідно, в точках 1 і 2, Н/Кл; l – відстань між точками, м.

1.8. Поняття про моделювання електричних полів

Силові лінії можуть мати точки, у яких електричний потенціал для всіх них має однакове значення. Уявна поверхня, проведена в просторі через такі точки, називається еквіпотенціальною поверхнею. Силові лінії та еквіпотенціальні поверхні електричного поля, створеного двома точковими зарядами, зображені нарис. 1.2. Еквіпотенціальні поверхні в будь-якій точці є перпендикулярні до силових ліній.

Представлена на рис. 1.2. модель електричного поля показує принцип побудови картини електричного поля для двох точкових зарядів. Переміщення зонда при незмінній величині вимірюваного ним потенціалу визначає координати еквіпотенціальної лінії чи поверхні.

На практиці часто приходиться мати справу із складними конфігураціями електричних полів. Прикладом цього може бути електричне поле зарядженої поверхні із складним рельєфом, електричне поле з об’ємним зарядом та ін. У таких випадках наведений метод із "зондуванням" поля є єдиним шляхом встановлення його картини у просторі.

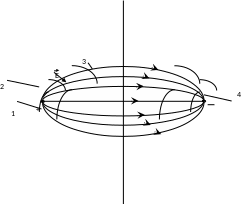
Рис. 1.2. Силові лінії та еквіпотенціальні поверхні електричного поля двох точкових зарядів

1- позитивний точковий заряд; 2 - еквіпотенціальна поверхня; 3 - силова лінія; 4 – негативний заряд; – вектор напруженості електричного поля.

1.9. Напруженість електростатичного поля як градієнт потенціалу.

Розглянемо дві еквіпотенціальні поверхні, потенціали яких дорівнюють відповідно j₁ і j₂ (рис 1.3). При цьому приймемо, що j₁>j₂. Поверхні j₁ і j₂ розташовані на такій відстані, що напруженість у взятих на них точках 1 і 2 має однаковий напрямок, який визначає одиничний вектор 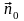. Різниця потенціалів, або електрична напруга між точками 1 і 2 буде

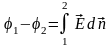, (1.17)

де , 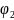– _{електричні потенціали, відповідно, в точках електричного поля 1 і} 2, В; 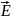– середнє значення напруженості електричного поля між точками 1 і 2; 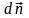– вектор, модуль якого дорівнює відстані n між точками 1 і 2, а напрямок співпадає із напрямком вектора .

_{Прийнявши n → dn, можна записати}

(1.18)

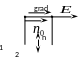
Рис. 1.3. Напруженість і градієнт потенціалу електричного поля

1 і 2 – точки на еквіпотенціальних поверхнях, що мають спільну нормаль; n – відстань між точками 1 і 2; – одиничний вектор, направлений по напрямку напруженості поля ; grad j – градієнт потенціалу.

Таким чином

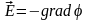. (1. 19)

Отже, напруженість електричного поля в якій-небудь точці дорівнює швидкості зміни потенціалу в цій точці, взятій з протилежним знаком.