3.3. Закон неперервності магнітного потоку

Закон неперервності магнітного потоку в інтегральній й формі запису

Магнітний потік, який увійшов всередину будь-якого об’єму, дорівнює магнітному потоку, що вийшов із цього об’єму

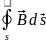= (3.11)

Таким чином алгебраїчна сума потоків, що увійшли в будь-який об’єм, дорівнює магнітному потоку, який вийшов із того ж об’єму.

Закон неперервності магнітного потоку в диференціальній формі запису

У будь якій точці магнітного поля немає ні джерела ні стоку вектора магнітної індукції.

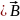= 0 (3.12)

Отже лінії вектора магнітної індукції є замкненими. Вони ніде не перетинаються і не перериваються. Тому для сукупності точок, де щільність струму відсутня, на підставі (2.18) і (2.19) даний закон може бути представлений також рівнянням Лапласа (2.20) для магнітного поля

=0

Електромагнітне поле в однорідному середовищі не зазнає змін з боку його магнітної складової

3.4. Теорема Гауса

Теорема Гауса в інтегральній й формі запису

Потік вектора електричного зсуву через будь яку замкнуту поверхню, що оточує даний об’єм, дорівнює алгебраїчній сумі зарядів, що знаходяться усередині цієї поверхні

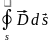= , (3.13)

де 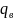– вільний електричний заряд, Кл.

Теорема Гауса у формі (3.13) вважається справедливою для будь якого матеріального середовища.

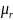Враховуючи, що = за умови, що = const, дану теорему можна записати у такій формі:

Потік вектора напруженості електричного поля крізь будь яку замкнуту поверхню, що оточує даний об’єм, дорівнює сумі вільних зарядів, що знаходяться усередині цієї поверхні, поділеній на абсолютну діелектричну проникність.

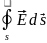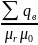= , (3.14)

Теорема Гауса для потоку вектора напруженості електричного поля у формі (3.14) можна вважати достовірною для однорідних ізотропних матеріальних середовищ.

Для сфери навколо точкового заряду в однорідному середовищі теорема Гауса в інтегральній й формі запису має вигляд

= , (3.15)

Враховуючи, що =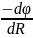 , можна знайти потенціал заряду на відстані

від його центру

= + C, (3.16)

де C – стала інтегрування, з точністю до якої визначається

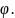
У випадках неоднорідних анізотропних матеріальних середовищ, потік вектора створюється не тільки сумою вільних зарядів, але і розташуванням зарядів зв’язаних, які знаходяться усередині цієї поверхні.

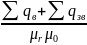= , (3.17)

де – алгебраїчна сума зв’язаних зарядів, які формують потік вектора Кл.

Теорема Гауса в диференціальній й формі запису

Джерело ліній вектора електричної індукції у будь якій точці електромагнітного поля визначається щільністю зарядів в цій точці.

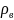= , (3.18)

де , – щільність вільних зарядів в точці поля, Кл/м³.

При 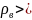0 лінії вектора виходять із точки, а при 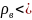0 – входять в неї.

Для однорідного середовища (3.18) можна представити так

= , (3.19)

або за умови, що const можна записати 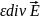= . Тоді

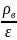= , (3.20)

Для неоднорідного середовища 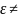const і замість (3.20) буде

= , (3.21)

де щільність зв’язаних зарядів

Наведені вище чотири рівняння електромагнітного поля носять також назву рівнянь Максвелла.