Розділ 3. Основні закони електромагнітного поля

До основних законів (рівнянь) електромагнітного поля належать: закон повного струму; закон електромагнітної індукції, теорема Гауса, закон неперервності магнітного потоку, теорема Умова-Пойтінга та деякі інші закономірності. Закони електромагнітного поля представляють у інтегральній та диференціальній формах. Перші чотири закони називають також рівняннями Максвелла. В деяких випадках в літературних джерелах до рівнянь Максвелла відносять тільки диференціальні форми запису вказаних законів. Деколи Максвеллу приписують тільки перші два закони. Це хоча і має певні історичні підстави, але для логічного сприйняття важливого для фахового формування навчального матеріалу в посібнику всі чотири рівняння, доповнення до них, а також теорему Умова-Пойтінга представлено як основні закони електромагнітного поля.

3.1. Закон повного струму

Закон повного струму в інтегральній формі запису.

Лінійний інтеграл від напруженості магнітного поля уздовж будь якого замкнутого контуру дорівнює величині струму усередині цього замкнутого контуру

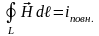(3.1)

Повний струм складається із струму електропровідності, струму переносу(зсуву) в матеріальному діелектричному середовищі та струму зсуву у вакуумі.

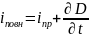, (3.2)

де 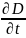– струм зсуву в діелектричному середовищі та вакуумі, А.

Закону повного струму в диференціальній формі запису.

Ротор (вихор) вектора напруженості магнітного поля дорівнює щільності повного струму провідності та струму зміщення

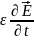
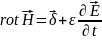, (3.3)

_{де – щільність струму провідності, А/м2.}

, (3.4)

При вирішенні ряду практичних задач можна вважати, що

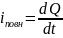, (3.5)

де – уявний повний електричний заряд, який міг би створити своїми змінами в часі і просторі заданий вихор магнітного, або який у відповідному стані є наслідком такого вихорю.

Часткові похідні в представлених вище і у всіх наступних даного розділу математичних виразах засвідчують, що рівняння електромагнітного поля складені для умов, при яких тіла і контури, в яких відбуваються описувані процеси, є нерухомі стосовно прийнятої просторової системи відліку (системи координат).

3.2. Закон електромагнітної індукції

Закон електромагнітної індукції в інтегральній формі запису

Лінійний інтеграл від напруженості електричного поля уздовж будь якого замкнутого контуру дорівнює швидкості зміни в часі магнітного потоку усередині цього замкнутого контуру

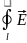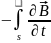d = d , (3.6)

Ліва частина рівняння (3.6) представляє собою електрорушійну силу в контурі при пронизуванні охоплюваної ним площі магнітним потоком, індукція В кого відома. Тобто

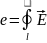d , (3.7)

де е – електрорушійна сила згаданого вище контуру, В.

Права частина представленого в (3.6) закону є швидкістю зміни в часі магнітного потоку Ф

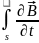d = (3.8)

У такий спосіб закон електромагнітної індукції в інтегральній формі запису (3.6) може бути представлений

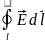= (3.9)

Інтегральна форма запису закону електромагнітної індукції покладена в основу опису роботи електромагнітних генераторів вироблення електричної енергії, а також електричних машин і апаратів.

Закон електромагнітної індукції в диференціальній формі запису

Ротор (вихор) вектора напруженості електричного поля дорівнює швидкості зміни вектора магнітної індукції, взятій зі знаком «мінус»

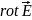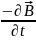= (3.10)

Фізичний зміст диференціальної форми цього закону полягає в тому, що будь яка зміна магнітного поля за часом 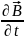у якій-небудь точці поля збуджує вихор електричного поля в цій же точці. Тобто у всіх випадках зміна магнітного поля викликає вихрове електричне поле.