4.3. Линейный множественный регрессионный анализ

В практике часто возникают ситуации, когда функция отклика (цели) У зависит не от одного, а от многих факторов. Установление формы связи в этих случаях начинают, как правило, с рассмотре­ния линейной регрессии вида

В этом случае результаты наблюдений должны быть представле­ны уравнениями, полученными в каждом из п опытов:

(4.35)

Или в виде матрицы результатов наблюдений

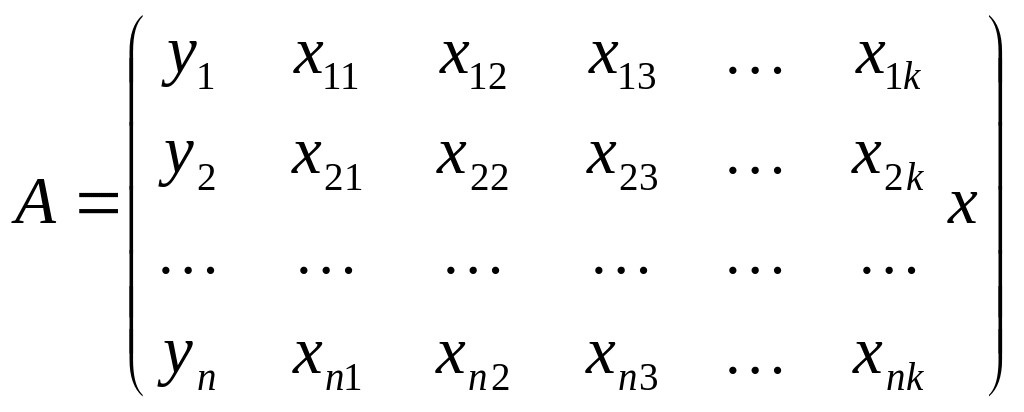
где п — количество опытов;

к — количество факторов.

Для решения системы уравнений (4.35) необходимо, чтобы ко­личество опытов было не менее к + 1, т.е. п> к +1,

Задачей множественного регрессионного анализа является по­строение такого уравнения прямой в -мерном пространстве, от­клонения результатов наблюдений от которой были бы минимальными. Использую для этого метод наименьших квадратов, получаем систему нормальных уравнений:

которую представим в матричной форме

(4.37)

где - вектор-столбец коэффициентов уравнения регрессии;

-матрица значений факторов;

вектор-столбец функции отклика;

- транспонированная матрица

При они соответственно равны:

; ; .

Умножая правую и левую части уравнения (4.37) на обратную матрицу получим при

откуда

(4.38)

Каждый коэффициент уравнения регрессии вычисляется по формуле

(4.39)

где элементы обратной матрицы

Пример 4.8. В результате проведенных исследований влияния на прибыль (Y) величины затрат на рекламу и создание сети дистрибьюторов получены уравнения:

Установить форму связи прибыли с факторами Х\ и Х₂ в виде линейного уравнения регрессии.

Решение. Представляем результаты опытов в виде матриц:

; ; ;

; .

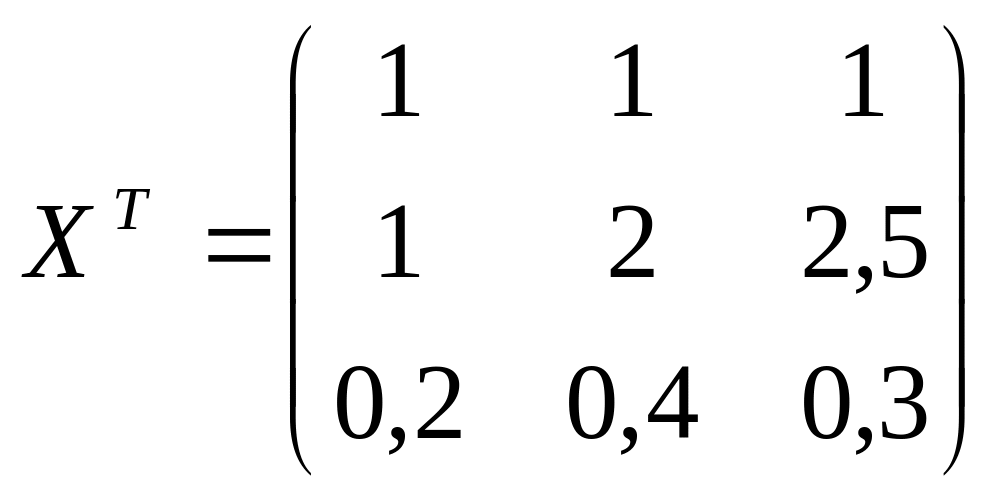Определяем коэффициенты уравнения регрессии

Получим уравнение регрессии у =14 + 2х₁ + 12х₂. ►

Для проверки значимости уравнения регрессии необходимо при заданных значениях провести несколько экспериментов, чтобы получить некоторое среднее значение функции Y. В этом случае экспериментальный материал представляется, например, в виде табл. 4.7.

№	Уровни факторов		Значение функции Y при параллельных опытах			Опытное среднее значение у,
	х\	х2	У\	>’2	Уз
1	1,0	0,2	18,2	18,6	18,7	18,5
2	2,0	0,4	21,6	23,4	23,7	22,9
3	2,5	0,3	22,0	23,0	22,5	22,5

Число параллельных опытов, как.правило, должно быть более трех

Р Проверка значимости уравнения регрессии проводится но F-критерию. Для этого вычисляется остаточная дисперсия

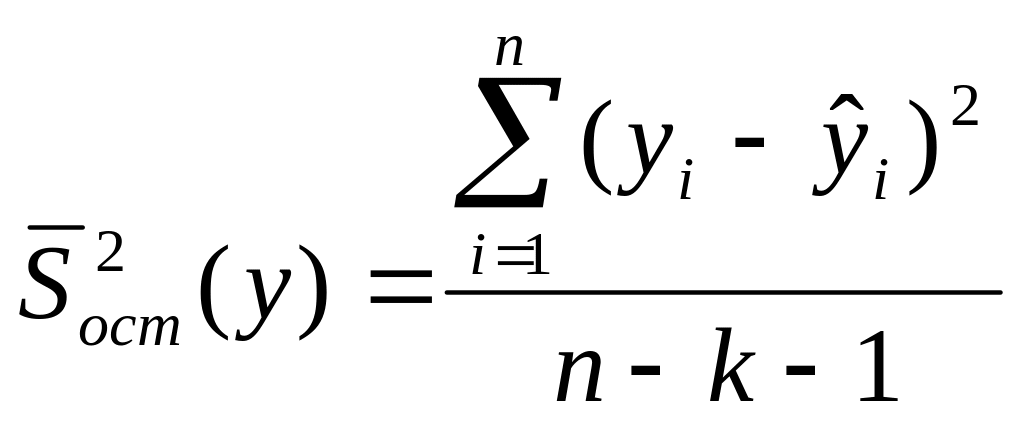
и статистика

которая сравнивается с табличным значением при уровне значимости

и числе степеней свободы (определяется по таблицам Фишера).

Гипотеза о значимости уравнения регрессии принимается при условии

.

Значимость коэффициентов регрессии проверяется по критерию.

Статистика сравнивается с табличным значением при уровне значимости и числе степеней свободы ( определяется по таблицам Стьюдента).

Погрешность коэффициента регрессии

(4.40)

где диагональный элемент матрицы

Доверительный интервал для коэффициентов регрессии определяется по формуле

(4.41)

где B- значение коэффициента регрессии в генеральной совокупности.

Пример 4.9. По данным табл. 4.7 получено уравнение регрессии Проверить значимость уравнения регрессии.

Решение. Данные табл. 4.7 представим в виде, удобном для вычислений (табл. 4.8).

Определим остаточную дисперсию.

Дисперсия для

Номер опыта	Уровни (рак то­ров		Значение функции		Опытное среднееV,	Значение Уiuiуравнения регрессии	(>’ - 3’,)	(У,“ V, У
	х\	х7	У/	2 У<
1			18,2	331,24			-0,2	0,04
2	1,0	0,2	18,6	345,96	18,5	18,4	0,2	0,04
3			18,7	349,69			0,3	0,09
4			21,6	466,56			- 1,2	1,44
5	2,0	0.4	23,4	547,56	22,9	22,8	0,6	0,36
6			23,7	561,69			0,9	0,81
7			22,0	484,00			- 0,6	0.36
8	2,5	0,3	23,0	529,00	22,5	22,6	0,4	0.16
9			22,5	506,25			- 0,1	0,01
Сумма			191,7	4121,95				3,31

Таблица 4.8.

Вычислим статистику:

При уровне значимости и числе степеней свободы и (приложение 8) находим

Так как

то гипотеза о значимости уравнения регрессии принимается.

40