L7. Work, Energy and Linear Momentum

Concept of Work Done: Transfer of energy to a system by an external force.

For constant force:

For variable force:

Work-Kinetic Energy Theorem

The total work done by the net external force on a system or object equals the change in kinetic energy (KE) of the system or object. (proof)

Instantaneous Power: the energy transfer rate or work done per unit time

Average Power: The total energy transferred or work done over the total time

if is constant and in the same direction as

Kinetic Energy (KE):

Potential Energy (PE): “stored” energy retrievable at a later time. It depends on the:

1. relative positions of masses or electric charges in a force field;

2. masses or charges in a force field;

3. magnetic or nuclear properties of particles in the force field.

• Reference position: is chosen. The PE is calculated relative to a reference level or position;

• The PE of an object in the force field is equal to the work required to take the object from the reference position to its position in the field;

In any isolated system of objects interacting only through conservative forces, the total mechanical energy of the system E = KE + PE is constant in time (conserved)

The total mechanical energy is the sum of kinetic energy (KE) and potential energy (PE). It does not include heat loss or work done by friction;

The total energy E might change form in time, but its numerical value remains the same;

There are no external forces in an isolated system, only internal forces.

Momentum and Impulse

Momentum: =m

Impulse – is a change in momentum Δp

“In an isolated system the total momentum is constant at any time” OR “In an isolated system the change in total momentum is zero”

• A collision is elastic if the KE and momentum are conserved;

• Momentum may be conserved, but the KE is not conserved in inelastic collisions.

L8. Conservative and Non-conservative Forces. Potential Energy Functions

Conservative Forces

• The work done by a conservative force in moving a particle between any two points is path independent.

• Total energy is conserved in a conservative force field.

Where the circle in the above integral indicates a closed path.

Non-conservative Forces

• Energy is lost from (not conserved in) a system subject to or interacting through non-conservative forces;

• Energy is not conserved in a non-conservative force field.

Examples: friction, air drag, viscous forces, electric forces in the presence of time-varying magnetic fields.

Conservative Forces and Potential Energy

• Define a potential energy function U(r) such that:

• W_C is work done by the conservative field force

• ΔU is negative when and (displacement vector) are in the same direction, e.g. mass lowered in a gravitational field

• The conservative force is related to the potential energy function by:

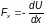
Stable Equilibrium – U(x) has a minimum value when F(x) = 0.

Unstable Equilibrium – U(x) has a maximum value when F(x) = 0.

L9. Torque

Torque

Torque, τ, is the tendency of a force to rotate an object about some axis. Therefore, a torque (also called ‘moment’ of a force) gives a measure of how much ‘turning effect’ a force has about a given axis.

The direction of  is perpendicular to the plane of r and F.

The direction is given by the thumb when using the right hand rule

A couple is a special case of a torque with two equal but oppositely directed parallel forces acting at different points of a body.

• A couple acts on a rigid body, that is, a body in which none of the internal parts move relative to one another.

• Note 1: We can consider torques about any point between the forces.

• Note 2: Although there is no resultant force, there will be acceleration

Condition for equilibrium

• Sum of all forces applied on a mass should be zero: ΣF = 0

• The sum of torques acting to give a clockwise rotation should equal the sum of torques acting to give an anti-clockwise rotation: Σ = 0

Center of mass of the body

• The object is divided up into a large number of very small particles of weight (m_ig)

• Each particle will have a set of coordinates indicating its location (x_i,y_i) with respect to some origin.

• We wish to locate the point of application of the single force whose magnitude is equal to the weight of the object, and whose effect on the rotation is the same as that of all the individual particles.

• This point is called the center of mass of the object.