Раздел I. Физические основы классической механики

1. Кинематика материальной точки и абсолютно твёрдого тела

Механика. Представление о свойствах пространства

Механика – раздел физики, изучающий механическое движение, т. е. изменение положения тела в пространстве относительно других тел с течением времени.

Система отсчёта – тело отсчёта, система координат, выбранный способ измерения времени.

При этом должны быть заданы свойства пространства:

1. однородность, т. е. все точки пространства эквивалентны;

2. изотропность, т. е. все направления пространства эквивалентны;

3. все точки пространства обладают евклидовой геометрией, т. е. точки пространства не пересекаются.

ПДСК (прямоугольная декартовая система координат)

← разложение вектора по базису

x, y, z – длины составляющих на соответствующие оси

Векторные величины

Векторная величина – направленный отрезок, который характеризуется точкой приложения, направлением в пространстве и модулем.

Сложение векторов:

• по правилу треугольника

• по правилу параллелограмма

Вычитание векторов:

Умножение вектора на число:

Скалярное произведение векторов:

Векторное произведение векторов:

Для нахождения направления вектора пользуются правилом правовинтового буравчика:

Если вращать рукоятку буравчика по кратчайшему расстоянию от первого вектора ко второму, то остриё при этом укажет направление результирующего вектора.

Модуль результирующего вектора равен площади параллелограмма, построенного на векторах и .

Кинематика. Основные кинематические характеристики

Кинематика – раздел механики, изучающий движение тел в пространстве и во времени без учета причин (сил), вызывающих это движение.

– перемещение, – путь

Средняя векторная скорость:

Средняя путевая скорость:

Среднее векторное ускорение:

Мгновенное значение скорости и ускорения:

Прямая и обратная задачи кинематики

1) Прямая задача

Прямая задача кинематики решается дифференцированием.

2) Обратная задача (основная):

– дифференциал 2-го порядка

Чтобы найти закон движения, следует это выражение проинтегрировать дважды, с точностью до начальных постоянных:

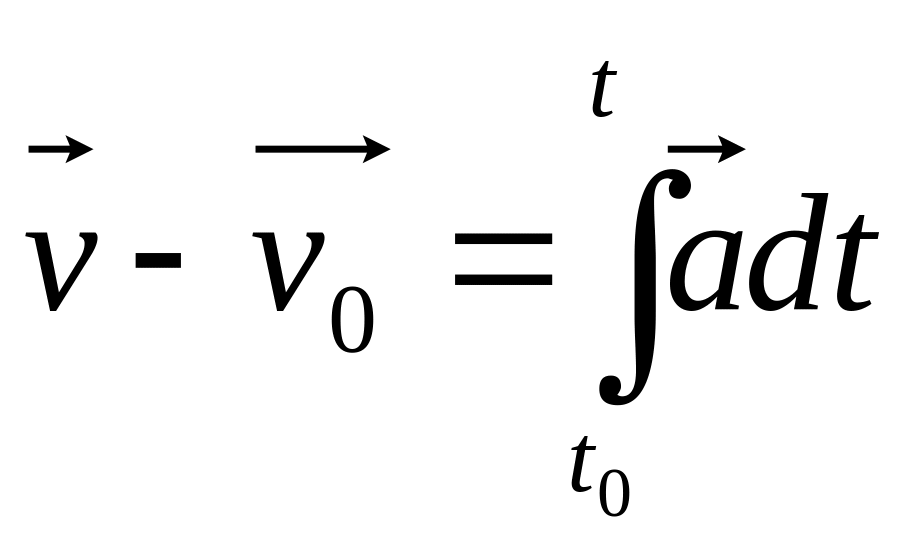
Кинематика вращательного движения

Тангенциальное и нормальное ускорение

Вспомним, что мгновенная скорость сонаправлена с вектором касательной траектории (единичный вектор касательной траектории )

I)

Тангенциальное ускорение характеризует изменение скорости по величине и сонаправлено с вектором касательной к траектории при ускоренном движении и противоположно направлено при замедленном движении.

II) – нормальное ускорение , где – единичный вектор нормали

Нормальное ускорение характеризует изменение скорости по направлению и направлено по нормали к центру мгновенной окружности:

Движение материальной точки по окружности. Угловая скорость

Если угол поворота бесконечно мал, то имеем дело с вектором.

Направление этого элементарного угла поворота задаётся правилом правовинтового буравчика:

Если направление рукоятки указывает обращение радиуса окружности, то при этом остриё, располагающееся перпендикулярно плоскости вращения, укажет направление угла .

Угловая скорость – величина векторная.

– связь угловой скорости и периода

Пусть

– среднее значение угловой скорости

Связь линейной и угловой скоростей

– мал, =>

Учитывая направление, получим:

Угловое ускорение. Связь между линейным и угловым ускорениями

Угловое ускорение – векторная величина

– угловое ускорение (мгновенное)

Угловое ускорение характеризует изменение угловой скорости.

Покажем связь между линейным и угловым ускорениями: