Тест Гольфельда-Куандта для перевірки гетероскедантичності моделі.
Завдання:
Перевірити чи залишки гомоскедантичні
чи гетероскедантичні та знайти матриці
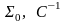використовуюси тест Гольфальда-Квандта.
Існує два варіанти тесту Гольдфельда-Квандта.
а) У першому варіанті :
Спостереження сортуємо по змінні - пояснююча змінна, від якої гіпотетично залежить умовна дисперсія залишків.
Всі спостереження
ділять
на дві групи об’ємом
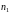та
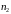(пополовині)
. Припускається, що збурення спостережень
в 1-ій групі мають меншу дисперсію, ніж
у другій.Для кожної із груп будуть лінійні рівняння регресії
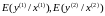за допомогою МНК.В кожній із груп знаходять залишки
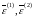.Обчислюють статистику:
(5)Дана статистика (5) є статистикою Фішера
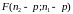роподіленою.
Ставимо нульову гіпотезу
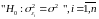(залишки
однакові- існує гомоскедантичність ).Гіпотеза відхиляється, якщо
-
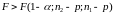критичне значення статистики Фішера
обчислене за таблицями.
Тест може бути застосований, якщо:
*)
; **)
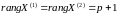
В
цьому випадку
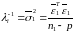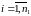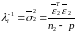для
,
для
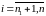
Улммр з автокорельваними залишками (побудова матриць ).
В найпростішому випадку при автокореляції збурень в регресійному рівнянні (при автокореляції) має місце автокореляіцйна залежність між збуреннями першого порядку:
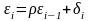(1)
де
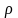- деяке число,
,
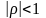а випадкові величини
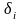задовільняють вимоги до залишків
класичної моделі:
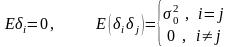(2)
(вважається, що співвідношення (11.1) справедливе для любого "моменту часу" і скільки завгодно віддаленого в майбутнє чи минуле, тобто і може пробігати всі цілочислові значення від -∞ до +∞)
Визначимо
в цьому випадку
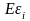і
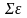(середнє значення і коваріаційну
матрицю). З (11.1) випливає :
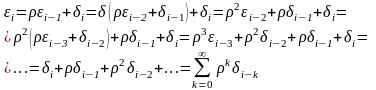(3)
З (11.3) з врахуванням (11.2) випливає :
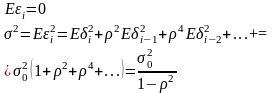(4)
Для
обчислення коваріацій
запишемо добуток з врахуванням (11.3)
у вигляді :
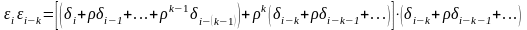Враховуючи,
що із взаємної корельованості
випливає взаємна некорельованість
величин
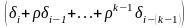і
,
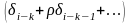дістаємо:
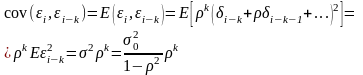(5)
Отже матрия в даній моделі має вигляд:
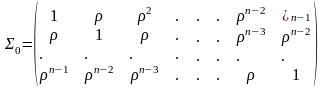(6)
Обернена
матриця
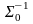має вигляд:
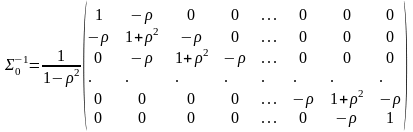(7)
УЛММР перетворюється в класичну шляхом домноження на матрицю перетворень С. Для моделі з автокореляцією першого порядку матриця С може бути вибрана у вигляді :
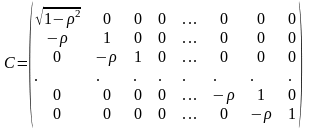(8)
Зауважимо, що у випадку циклічних коливань у спостережених даних можуть бути розглянуті автокореляційні процеи більш високого порядку. Наприклад, при обробці піврічних даних за наявності в них сезонних коливань природними є автокореляції залишків другого порядку :
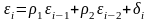
(збурення
при цьому вільні від автокореляції,
якщо
).
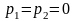При роботі з квартальними даними може бути доіцльним розгляд авторегресійного процесу четвертого порядку :
