Коваріаційна матриця мнк – оцінок.
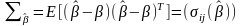
З
допомогою
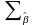підраховують основні показники варіацій
оцінок
біля істинних значень і одночасно
характеристики оцінок:
діагональні елементи задають середні квадрати відповідних оцінок
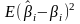(це є дисперсії оцінок)
-
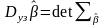узагальнена дисперсія (визначається,
як визначник коваріантної матриці)степінь тісноти парних лінійних зв’язків між компонентами
(
)
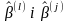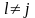визначає коефіцієнт кореляції
,
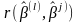який визначається через елементи
коваріаційної матриці
.
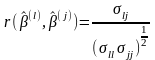Обчислимо коваріаційну матрицю
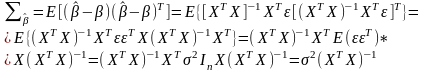(5)
Зауважимо, що в практиці часто користуються не самою матрицею, а її оцінкою
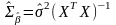(6)
де визначається (5.4).
Маючи
(5.6) можна обчислити середньоквадратичне
відхилення
,
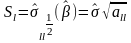де
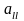діагональні елементи матриці
.
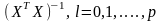Перевірка наявності зв’язку між екзогенними і ендогенною змінними за критерієм Фішера. Перевірка значимості коефіцієнтів моделі за критерієм Стьюдента.
Узагальнення теореми Фішера
є
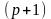-мірно
нормально розподіленою випадковою
величиною, з вектором середніх значень
рівним істинним значенням аналізованих
параметрів
,
і з коваріаційною матрицею
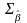(5.6), тобто
(5.10)випадкова величина
є
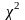-розподіленою
з
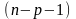степенями свободи, тобто
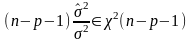(1)
оцінки і є статистично незалежними.
Наслідок з теореми Фішера.
Нехай
- істинне (гіпотетичне) значення
го
коефіцієнта регресії моделі .
Тоді статистика
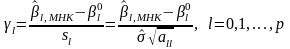(2)
розподілена
по закону Стьюдента (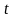
-розподіл)
з
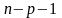степенями свободи.
95%
інтервал довіри в границях
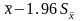до
.
-
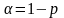рівень значимості.
Для нормального розподілу:
- відповідає інтервалу довіри.
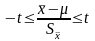
Правило
перевірки гіпотез виду
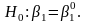
Нехай
-
задане гіпотетичне значення
-того
коефіцієнта регресії. По заданому рівні
значимості критерію
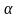з таблиць процентних точок
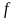розподілу знаходимо
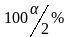точку розподілу Стьюдента з
ступінню свободи
.
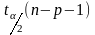Якщо
,
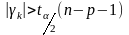то гіпотезу
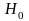відкидаємо. В протилежному випадку
)
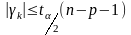гіпотеза
не відкидається. В поширеному частковому
випадку перевірки гіпотези
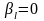рішення про прийняття чи відхилення
даної гіпотези приймається на основі
порівняння величини
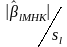із значенням
;
при
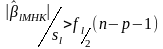гіпотеза
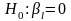відкидається.
Побудова
інтервала довіри для невідомого значення
коефіцієнта регресії
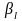
З
(5.12) випливає, що з імовірностю
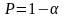істинне значення
-го
коефіцієнта регресії повинно задовільняти
нерівності
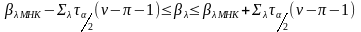(3)
Перевірка гіпотези про відсутність будь-якого лінійного зв’язку між і сукупністю пояснюючих змінних . В припущенні справедливості гіпотези
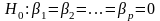
(проти
альтернативної гіпотези
:
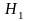хоча б одне з
відмінне від нуля)
статистика
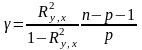розподілена згідно
-
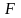розподілу з числами степеней свободи
чисельника і знаменника рівними
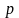і
відповідно. Тому гіпотезу
можна перевірити наступним чином. По
заданому рівню значимості критерія
визначаємо з таблиць
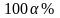-нту
точку
розподілу
.
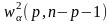Якщо
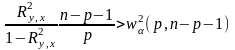(4)
то гіпотеза про відсутність лінійного зв’язку між і відкидається (з імовірністю помилитися, рівною ). В противному випадку - гіпотеза приймається