- •Класична лінійна модель множинної регресії (клммр)
- •В клммр досліджуються лінійні функції регресії (2)
- •Метод найменших квадратів (мнк) і метод максимуму правдоподібності.
- •Аналіз варіації результуючого показника
- •4.Оцінка якості статистичної моделі.
- •Статистичні властивості оцінок параметрів клммр. Обґрунтованість оцінок і .
- •Незміщеність оцінок.
- •Коваріаційна матриця мнк – оцінок.
- •Перевірка наявності зв’язку між екзогенними і ендогенною змінними за критерієм Фішера. Перевірка значимості коефіцієнтів моделі за критерієм Стьюдента.
- •Перевірка гіпотези про відсутність будь-якого лінійного зв’язку між і сукупністю пояснюючих змінних . В припущенні справедливості гіпотези
- •Мультиколінеарність та способи відбору найбільш суттєвих пояснюючих змінних.
- •3. Версія покрокового відбору змінних.
- •1) Версія всіх можливих регресій.
- •2) Версія покрокового підбору змінних.
- •Помилки специфікації клммр моделі, пов’язані із вибором пояснюючих змінних.
- •Узагальнена лінійна модель множинної регресії (улммр з гетероскедантичними та автокорельованими регресійними залишками).
- •Узагальнений метод найменших квадратів (умнк).
- •Тест Спірмана для перевірки гетероскедантичності моделі.
- •Тест Глейcера для перевірки гетероскедантичності моделі.
- •Тест Гольфельда-Куандта для перевірки гетероскедантичності моделі.
- •Улммр з автокорельваними залишками (побудова матриць ).
- •Статистика Дарбіна –Уотсона
- •17. Оцінка авторегресійного параметра в моделі з автокорельованими залишками.
- •18. Двокроковий метод Дарбіна оцінки авто регресійного параметру.
- •Нелінійні моделі. Деякі властивості нелінійних залежностей, які підлягають безпосередній лінеаризації (моделі гіперболічного, експоненціального, степеневого та логарифмічного типів.
- •20. Підбір лінеаризуючого перетворення (підхід Бокса-Кокса)галіме!!!!
- •Точковий прогноз та побудова інтервалів довіри прогнозу на основі регресійних моделей.
- •22. Дослідження точності моделі в реальній ситуації (розбиття вибірки на дві підвибірки, метод ”ковзного екзамену”).
- •Умови ототожнення слвр (умови 1,2,3).
- •Умови ототожнення окремого рівняння слвр (умови 4,5).
- •???26.Оцінювання структурних параметрів окремого рівняння двокроковим методом найменших квадратів.
Класична лінійна модель множинної регресії (клммр)
КЛММР
реалізує собою найпростішу версію вимог
до загального вигляду функції регресії
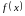 ,
природи пояснюючих змінних
,
природи пояснюючих змінних
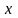 і статистичних регресійних залишків
і статистичних регресійних залишків
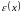 в загальній регресійній моделі.
в загальній регресійній моделі.
В рамках КЛММР ці вимоги формулюються наступним чином:
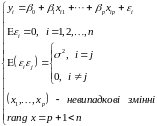 (1)
(1)
З (1) випливає:
В клммр досліджуються лінійні функції регресії (2)
де
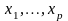 - невипадкові параметри, від яких залежить
закон розподілу імовірностей результуючої
змінної
- невипадкові параметри, від яких залежить
закон розподілу імовірностей результуючої
змінної
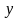 .
Це означає, що у вибіркових спостереженнях
.
Це означає, що у вибіркових спостереженнях
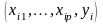 єдиним джерелом збурень значень
єдиним джерелом збурень значень
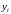 є збурення регресійних залишків
є збурення регресійних залишків
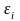 .
.
Постулюється взаємна некорельованість залишків (
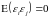 для
для
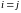 ).
Припущення відносно
).
Припущення відносно
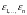 є основним припущенням КЛММР і є
природнім в широкому класі реальних
задач (особливо для просторових вибірок).
Це означає, що збурення, які отримуються
при спостереженнях над іншими і навпаки.
є основним припущенням КЛММР і є
природнім в широкому класі реальних
задач (особливо для просторових вибірок).
Це означає, що збурення, які отримуються
при спостереженнях над іншими і навпаки.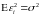 (не
залежить від спостереження ) означає
незміщеність дисперсій регресій них
залишків. Така властивість називається
гомоскедантичністю регресій них
залишків.
(не
залежить від спостереження ) означає
незміщеність дисперсій регресій них
залишків. Така властивість називається
гомоскедантичністю регресій них
залишків.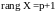 -
немає залежностей між змінними.
-
немає залежностей між змінними.
Запишемо модель (1) в матричній формі:
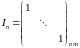
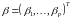 - вектор-стовпець невідомих значень
параметрів
- вектор-стовпець невідомих значень
параметрів
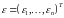 -
вектор – стовпець регресійних залишків
-
вектор – стовпець регресійних залишків
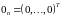 -
вектор нулів
-
вектор нулів
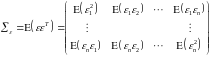 -
коваріаційна матриця
-
коваріаційна матриця
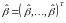 -
вектор оцінок невідомих параметрів
-
вектор оцінок невідомих параметрів
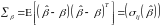 ,
,
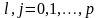 - коваріаційна матриця незміщених оцінок
- коваріаційна матриця незміщених оцінок
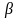 невідомих параметрів
невідомих параметрів
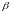 .
.
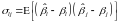
Тоді матрична форма КЛММР має вигляд
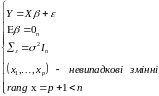 (1/)
(1/)
У
випадку, коли до умови (2.1) чи (2.1/)
постулюють нормальний розподіл
регресійних залишків
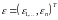 (що записуються у вигляді
(що записуються у вигляді
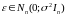 ),
тоді говорять що
і
зв’язані нормальною КЛММР. Метою
регресійного аналізу є визначення
(статистична оцінка) величини
і
),
тоді говорять що
і
зв’язані нормальною КЛММР. Метою
регресійного аналізу є визначення
(статистична оцінка) величини
і
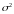 .
.
Метод найменших квадратів (мнк) і метод максимуму правдоподібності.
Основа
МНК: підібрати такі оцінки
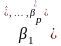 для невідомих значень параметрів
функції регресії
для невідомих значень параметрів
функції регресії
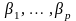 при яких регресійні значення результуючого
показника
при яких регресійні значення результуючого
показника
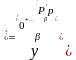 (1)
(1)
як
можна менше відрізняються від
спостережуваних величин
 .
Введемо за міру розбіжності різницю:
.
Введемо за міру розбіжності різницю:
 ,
(2)
,
(2)
де
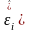 -нев'язка.
-нев'язка.
 Коефіцієнти
Коефіцієнти
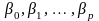 слід підбирати так, щоб вони мінімізували
деяку характеристику нев'язок. За таку
характеристику приймемо величину:
слід підбирати так, щоб вони мінімізували
деяку характеристику нев'язок. За таку
характеристику приймемо величину:
 (3)
(3)
Тоді
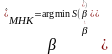 (4)
(4)
Запишемо
(2) в матричній формі:
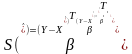 (5)
(5)
Запишемо
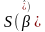 у вигляді :
у вигляді :
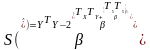 (5*)
(5*)
(величина
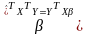 ).
).
Необхідні умови оптимальності мають вигляд:
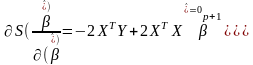 (6)
(6)
Відносно диференціювання:
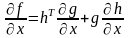
Тоді
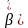 знаходиться із системи рівнянь
знаходиться із системи рівнянь
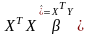 (7)
(7)
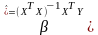 (8)
(8)
Запишемо
систему (6) для випадку парної регресії
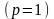 . В цьому випадку :
. В цьому випадку :
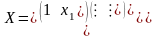 ,
,
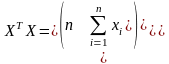 ,
,
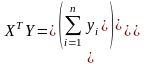
Тоді система (7) для матиме вигляд:
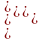 (9)
(9)
Якщо
додатково до умов КЛММР постулюється
нормальність регресійних залишків
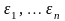 ,
то для оцінки параметрів
може бути застосований метод максимальної
правдоподібності (ММП) ( цей метод
застосовується, коли задається закон
розподілу імовірностей вибіркових
даних).
,
то для оцінки параметрів
може бути застосований метод максимальної
правдоподібності (ММП) ( цей метод
застосовується, коли задається закон
розподілу імовірностей вибіркових
даних).
В
цьому випадку (враховуючи некорельованість
залишків) функція правдоподібності в
термінах залишків
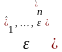 має вигляд:
має вигляд:
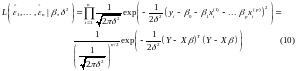 Оцінки
Оцінки
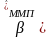 і
і
 визначають такі значення
і
визначають такі значення
і
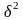 ,
при яких функція правдоподібності
,
при яких функція правдоподібності
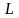 (або логарифмічна функція правдоподібності
(або логарифмічна функція правдоподібності
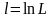 )
досягає своєї максимальної величини.
Тоді необхідні умови оптимальності для
логарифмічної функції правдоподібності
)
досягає своєї максимальної величини.
Тоді необхідні умови оптимальності для
логарифмічної функції правдоподібності
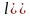 (10')
(10')
мають вигляд:
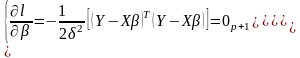 (11)
(11)
З першої умови знаходимо
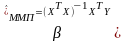 ,
(12)
,
(12)
що співпадає з оцінкою по МНК. Друга умова (11) дозволяє обчислити ММП-оцінку для :
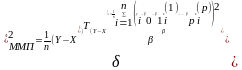 (13)
(13)