Лабораторна робота 10 аналітичне конструювання оптимального детермінованого регулятора для неперервних систем
Мета роботи – навчитися в пакеті MATLAB створювати аналітичну модель оптимального регулятора для неперервних систем та навчитись визначати показник якості.
Основні теоретичні відомості
Важливим аспектом у розробці систем управління є стійкість системи. Вона повинна бути забезпечена в усіх випадках використання системи.
Розглянемо питання поліпшення динамічних властивостей системи за допомогою зворотного зв’язку [10].
Розглянемо лінійну систему, яка описується диференціальним рівнянням
,
де
– вектор змінних стану системи,
– вектор змінних управління,
– матриця стану системи, розмірність
якої n,
–
матриця управління системи.
Керуюча змінна описується рівнянням
,
де
– вектор вимірюваних змінних,
– матриця спостереження, розмірність
якої
.
Допустимо,
що всі змінні вимірюються, тобто повний
стан
об’єкта управління може бути точно
виміряний у будь-який момент часу та
використаний для створення зворотного
зв’язку.
Отже,
на першому етапі синтезу оптимального
детермінованого регулятора слід задати
четвірку матриць, які описують стан
системи
,
причому, розмір матриці
має збігатися з розміром матриці
,
тобто
.
Матриця D здебільшого є нульовою.
Регулятор треба синтезувати для послідовного з’єднання об’єкта та виконавчого механізму, оскільки динаміка руху літака та рульових органів описується окремими системами рівнянь.
Розв’яжемо задачу побудови детермінованого оптимального регулятора, який мінімізує квадратичний інтегральний критерій
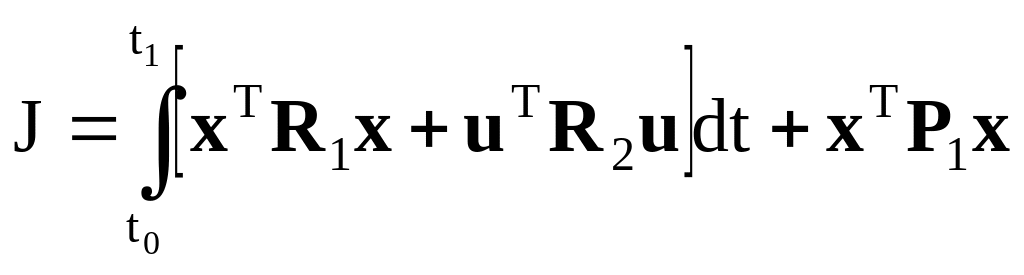, (10.1)
де
,
,
– невід’ємно визначені симетричні
матриці.
,
де
– додатна визначена симетрична матриця.
У критерії (10.1) перша складова
є мірою відхилення від нульового стану
системи в момент часу
.
Другий член критерію (10.1)
враховує витрати потужності на управління.
Термінальний член
входить до критерію, якщо потрібно
забезпечити максимальну близькість
термінального стану
до нульового значення.
Корінь квадратний із цього рівняння називається -нормою.
Оскільки
розглядається випадок, коли параметри
системи незмінні в часі, тобто
сталі, то можна представити інтегральний
квадратичний критерій у вигляді:
. (10.2)
Для мінімізації критерію (10.2) слід розв’язати рівняння Рікатті.
Знайдений
розв’язок
для даного випадку є сталим і є розв’язком
алгебраїчного рівняння Ріккаті
. (10.3)
Для цього рівняння отримаємо закон управління
,
де
.
Отже, на другому етапі синтезу мінімізується інтегральний квадратичний показник якості (10.2). Для цього задаються вагові коефіцієнти та , які враховують значення кожного з параметрів під час управління, та розв’язується алгебраїчне рівняння Ріккаті (10.3).
У
результаті синтезу отримуємо регулятор
у вигляді коефіцієнтів
,
при яких показник якості (10.2) буде мати
мінімальне значення.
У пакеті програм MATLAB можна побудувати оптимальний детермінований регулятор, використовуючи оператор lqr:
[F,P,E]=lqr(A,B,Q,R)
Для розв’язання цієї задачі треба задати вагові матриці Q, R (остання в цьому випадку – скаляр) та матриці об’єкта управління (A, B). Після виконання цього оператора отримуємо:
матрицю F оптимальних коефіцієнтів підсилення регулятора;
матрицю P, що є рішенням рівняння Ріккаті;
вектор Е, що містить власні числа матриці станів замкненої системи A-BF.
У пакеті програм MATLAB можна порахувати показник якості, використовуючи оператор normh2:
H2=normh2(Ao,Bo,Co,Do).