Порядок виконання роботи

1. Зібрати модель слідкуючої системи за схемою, що зображена на рис. 8.1.

Рис. 8.1.

Задати такі значення параметрів елементів: К₂=1; Т₃=0,1с; Т₄=0,2с; f₁=10В.

1. Зняти осцилограми перехідних процесів у системі при таких значеннях ширини лінійної частини характеристики нелінійного елемента: а₅=20; 10; 5 і 2.

2. Встановити стале значення а₅=2. Зняти осцилограму автоколивань у тій же системі при наступних значеннях сталої часу виконавчого двигуна Т₄=0,1; 0,2; 0,5; 1с.

3. Скориставшись методом гармонічного балансу (Гольдфарба-Попова), визначити за якого значення а₅ в системі виникнуть автоколивання, якщо параметри інших елементів відповідатимуть п.1. Порівняти отримане значення а₅ з результатами експерименту за п.2.

4. Зібрати модель релейної системи регулювання за схемою, яка зображена на рис. 8.2. Встановити такі значення параметрів елементів: К₆=2; К₇=0,5; Т₈=10с.

5. Зняти осцилограми автоколивань у системі за таких значень ширини петлі гістерезису: а₉=0,5; 2; 10 і при f₁=0В. Визначити масштаби, у яких знято осцилограми.

6. Встановити стале значення а₉=2, зняти осцилограми автоколивань у тій же системі за таких значень коефіцієнта підсилення: К₇=0,2; 1; 5 і при f₁=0В.

7. Задати постійне значення параметрів елементів К₆=2; а₉=2; К₇=0,5; Т₈=10с. Зняти осцилограми автоколивань у системі за таких значень зовнішнього впливу: f₁=0,5; 2; 10В.

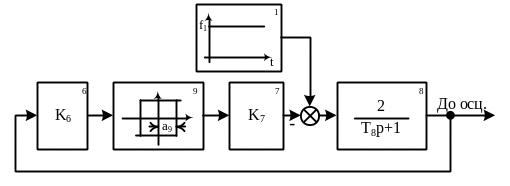Рис. 8.2.

Контрольні запитання

1. Які системи відносять до нелінійних?

2. Які характеристики відносять до істотно нелінійних?

3. На які групи поділяють методи аналізу нелінійних систем?

4. Який режим роботи нелінійної системи називається автоколивальним?

У чому полягає суть методу гармонічного балансу, які його переваги та недоліки?

Лабораторна робота 9 відновлення стану системи. Оптимальний стохастичний спостерігач (фільтр калмана)

Мета роботи – навчитись відновлювати вектор стану системи при стохастичних збуреннях за допомогою стохастичного спостерігача (фільтр Калмана).

Основні теоретичні відомості

Припустимо, що рівняння реальної системи має вид

, (9.1)

. (9.2)

Через позначається шум, який збурює стан, а через - шум спостережень чи вимірювань.

Отже, на першому етапі слід задати матриці системи в просторі станів, а також матриці коваріацій шумів стану та вимірювань [10].

Розглянемо випадок синтезу оптимального стохастичного спостерігача для літального апарата. Стан системи збурюється турбулентністю атмосфери, яка є кольоровим шумом. Стандартна задача синтезу оптимального стохастичного спостерігача припускає, що на систему діє білий шум. Для приведення поставленої задачі до стандартного вигляду варто включити формуючий фільтр (фільтр, на вхід якого надходить білий шум , а на виході є кольоровий шум , спектральні щільності якого описують турбулентність атмосфери) до структури об’єкта (тобто розширити об’єкт). Тобто, для синтезу ми використовуватимемо об’єкт з розширеним простором стану, що описується матрицями .

Припустимо, то спостерігач повного порядку типу

відповідає системі, що описується рівняннями (9.1), (9.2).

Тоді помилка відновлення визначається виразом

. (9.3)

Задача оптимального вибору величини називається задачею оптимального спостереження (задачею побудови оптимального спостерігача), тобто нам необхідно вибрати такі коефіцієнти спостерігача, щоб мінімізувати вираз (9.3).

Матрицю можна отримати, вирішивши алгебраїчне рівняння Ріккаті для спостерігача

,

де – розв’язок рівняння Ріккаті; , – інтенсивності білого шуму.

Тоді матриця коефіцієнтів підсилення оптимального спостерігача дорівнюватиме

Отже, на другому етапі здійснюємо синтез фільтра Калмана [10].

У результаті синтезу отримаємо спостерігач, що описується четвіркою матриць у просторі стану, на виході якого маємо відновлений вектор стану системи.

Схему з’єднання об’єкта зі спостерігачем зображено на рис.9.1.

Р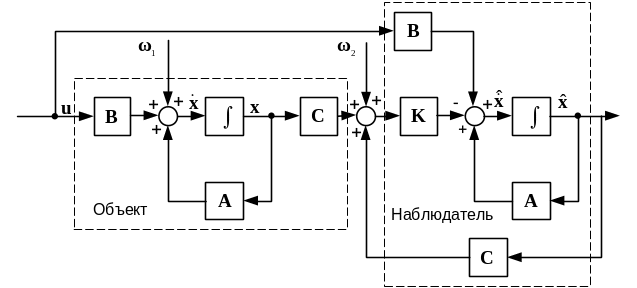 ис.9.1. Схема з’єднання об’єкта з оптимальним стохастичним спостерігачем