3.5 Сили пружності. Закон Гука для деформації розтягування (стискування)

Деформацією називається зміна форми, або розмірів тіла під дією зовнішніх сил. Розрізняють два ідеальних види деформацій: абсолютно пружні і абсолютно пластичні. При абсолютно пружній деформації форма і розміри тіла повністю відтворюються після припинення дії зовнішньої сили. При абсолютно пластичній, навпаки, форма і розмір тіла після припинення дії сили повністю зберігають набутий при деформації стан.

Сили, які виникають при пружних деформаціях, називаються пружними силами. Деформації бувають: розтягування (стискування); згинання; закручування; зсуву. Різні види деформацій можна звести до двох основних: розтягування (стискування) і зсув.

Розглянемо спочатку деформацію розтягування (стискування). Англійський фізик Р.Гук у 1660 році експериментально встановив закон, який носить його ім’я: при малих пружних деформаціях сила пружності пропорційна величині деформації

, (3.6)

k – коефіцієнт жорсткості, - величина деформації. Знак (-) мінус вказує, що сила пружності направлена в сторону, протилежну деформації, тобто має такий напрямок, щоб зменшити деформацію.

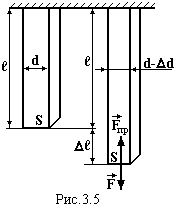
Нехай стержень довжиною ℓ площею перерізу S і поперечним розміром d закріплений за один кінець, а до другого прикладена розтягуюча зовнішня сила (рис.3.5). Внаслідок цього довжина стержня збільшується на величину ∆ℓ, а поперечний розмір зменшується на ∆d. Виникає пружна сила . Експерименти показують, що абсолютне видовження ∆ℓ прямо пропорційне силі , довжині стержня ℓ і обернено пропорційне площі перерізу S . (3.7)

Е – модуль пружності, або модуль Юнга, вимірюється в Н/м². Він характеризує пружні властивості матеріалу і являється величиною сталою для кожного матеріалу.

Відношення абсолютної деформації ∆ℓ до початкового розміру

називається відносною деформацією , величина безрозмірна.

Відношення сили F до площі поперечного перерізу S називається механічною напругою , вимірюється в Н/м². Рівняння (3.7) закону Гука приймає вид

. (3.8)

Механічна напруга пропорційна відносній деформації.

З’ясуємо фізичний зміст модуля Юнга Е. При ε = 1, тобто коли ∆ℓ = ℓ, Е = σ. Отже, модуль Юнга, це така механічна напруга, при якій довжина стержня подвоїться. Значення модуля Юнга можна знайти в довідникових таблицях.

Відношення зміни поперечного розміру ∆d до початкового значення d, тобто відносна зміна поперечного розміру, називається коефіцієнтом поперечного стискування .

Відношення коефіцієнта поперечного стискування ε_п до відносного видовження ε називається коефіцієнтом Пуассона

. Він також являється величиною сталою для кожного матеріалу і разом з модулем Юнга повністю характеризує пружні властивості речовини.

3.6 Закон Гука для деформації зсуву

Деформація зсуву виникає під дією сколюючої зовнішньої сили F, яка паралельна закріпленій площині (рис.3.6). Виникає пружна сила F_пр, яка паралельна площинам зсув і протилежна зовнішній силі. Експерименти показують, що абсолютний зсув ∆а прямо пропорційний зовнішній силі F, відстані ℓ між площинами ковзання і обернено пропорційний площі S площин ковзання

. (3.9)

G – модуль зсуву.

Відношення сколюючої сили до площі називається сколюючою механічною напругою, відношення абсолютного зсуву до відстані між площинами ковзання називається відносним зсувом . Отже, закон Гука для деформації зсуву прийме вид

. (3.10)

Сколююча напруга пропорційна відносному зсуву.

Модуль зсуву G – це така сколююча механічна напруга, при якій відносний зсув дорівнює 1, тобто . Це означає, що кут зсуву θ = 45^о. Модуль зсуву зв’язаний з модулем Юнга і коефіцієнтом Пуассона співвідношенням

. (3.11)