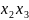Міністерство освіти і науки України

Київський Національний Університет технологій та дизайну

Кафедра електромеханічних систем

Лабораторне заняття №1

з навчальної дисципліни «Моделювання електромеханічних систем»

Тема: «Отримання математичної моделі за результатами експериментальних досліджень»

Варіант 21

Завдання 1. Виконати обробку результатів ПФЕ типу 2³ (за заданим варіантом) і знайти математичну залежність цільової функції Y від параметрів процесу Х1, Х2, Х3 (побудувати рівняння регресії).

Завдання 2. Виконати аналіз розрахованого рівняння регресії з метою отримання адекватної математичної моделі.

Завдання 3. Виконати перетворення факторів рівняння регресії до реальних (фактичних) величин за відповідними численними формулами переходу кожного фактора.

Виконав: студент групи БЕМч-12

Цуркан О.О.

Київ 2015

Початкові дані: Х₁₀ = 50; Х₂₀ = 100; Х₃₀ = 45;

∆Х₁/ Х₁₀ = 40%; ∆Х₂/ Х₂₀ = 20%; ∆Х₃/ Х₃₀ = 70%.

Досліди дублювалися рівномірно в кожній точці плану m = 3

Виконання завдання 1.

1) Розрахувати мінімальне та максимальне значення кожного фактора (параметра) в реальних (фактичних) одиницях вимірювання за умови, що значення Хі0 задано в реальних одиницях; позначити їх Х_{і мін} та Х_{і мах}.

Визначаємо значення інтервалу варіювання кожного фактора:

∆Х₁ = 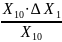= = 20 (H м);

∆Х₂ = = = 20 (В) ;

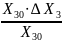∆Х₃ = = = 31,5 (А);

Розраховуємо значення Х_{і мін} та Х_{і макс}:

Х_{1 мін} = Х₁₀ - ∆Х₁ = 50 – 20 = 30 (H м);

Х_{1 макс} = Х₁₀ + ∆Х₁ = 50 + 20 = 70 (H м);

Х_{2 мін} = Х₂₀ - ∆Х₂ = 100 – 20 = 80 (В);

Х_{2 макс} = Х₂₀ + ∆Х₂ = 100 + 20 = 120 (В);

Х_{3 мін} = Х₃₀ - ∆Х₃ = 45 – 31,5 = 13,5 (А);

Х_{3 макс} = Х₃₀ + ∆Х₃ = 45 + 31,5 = 76,5 (А);

2) Скласти робочу матрицю експерименту. Позначити її «Таблиця 1»

Таблиця 1

Робоча матриця експерименту

№ досліду	Х1 (H м)	Х2 (В)	Х3 (А)	Yu1	Yu2	Yu3
1	70	120	76,5	86,02	89,62	88,82
2	30	120	76,5	75,5	74,93	76,76
3	70	80	76,5	57	57,46	57,2
4	30	80	76,5	68,25	68,11	68,57
5	70	120	13,5	84,62	84,42	84,2
6	30	120	13,5	72,46	74,72	76,5
7	70	80	13,5	60	60,1	60,77
8	30	80	13,5	67,84	67,02	67,1

3) Скласти розширену матрицю планування типу 23 та результатів розрахунків з врахуванням умов проведення паралельних дослідів. Позначити «Таблиця 2».

Таблиця 2

Матриця планування і результати розрахунків

№	Планування							Результат
								Y1	Y2	Y3
1	1	1	1	1	1	1	1	86,02	89,62	88,82
2	1	-1	1	1	-1	1	-1	75,5	74,93	76,76
3	1	1	-1	1	-1	-1	-1	57	57,46	57,2
4	1	-1	-1	1	1	-1	1	68,25	68,11	68,57
5	1	1	1	-1	1	-1	-1	84,62	84,42	84,2
6	1	-1	1	-1	-1	-1	1	72,46	74,72	76,5
7	1	1	-1	-1	-1	1	1	60	60,1	60,77
8	1	-1	-1	-1	1	1	-1	67,84	67,02	67,1