1. n-мерный вектор. Основные понятия: нулевой вектор, равенство векторов, ортогональные, сонаправленные, противоположно направленные, коллинеарные, компланарные вектора.

Любой упорядоченный набор из n действительных чисел называется n-мерным вектором или вектором в пространстве R ⁿ и обозначается в виде , а числа , составляющие этот набор, называются его координатами.

Вектор с нулевыми координатами называется нулевым вектором

Два вектора и называются равными, если равны их соответствующие координаты

Если векторы и перпендикулярны, то и . Тогда скалярное произведение =0. Векторы называются ортогональными, если их скалярное произведение равно нулю. Равенство =0 выражает условие перпендикулярности (ортогональности) двух векторов.

Если , то векторы и называются сонаправленными. В этом случае и

Векторы, лежащие на одной прямой или на параллельных прямых, называются коллинеарными.

Три вектора называются компланарными, если они лежат на одной плоскости или на параллельных плоскостях.

2)Операции над векторами.

Линейные операции над любыми векторами удовлетворяют следующим свойствам:

1⁰. 2⁰.

3⁰. 4⁰.

5⁰ 6⁰.

7⁰. 8⁰.

Суммой двух векторов одинаковой размерности n называется вектор ,

Произведением вектора на действительное число называется вектор , координаты , .

Скалярным произведением двух арифметических векторов называется число,: =

Скалярным произведением двух геометрических векторов и называется число, равное произведению длин этих векторов на косинус угла между ними: .

3)Модуль вектора

Длина (модуль) вектора определяется через проекции (координаты) по формуле : .

4)Условие коллинеарности, ортогональности и компланарности векторов.

Условие коллинеарности: Координаты этих векторов должны быть пропорциональны, т.е.

= = = к .

Условие ортогональности: Скалярное произведение векторов равно 0.

Условие компланарности:

1)Если смешанное произведение =0, то три вектора комплонарны.( Если три вектора комплонарны то и их смешанное произведение =0.)

2)Три вектора компланарны если они линейно зависимы.

5)Линейная комбинация системы векторов, линейная зависимость векторов.

Линейной комбинацией векторов (9) называется вектор вида

= ,где - любые действительные числа.

Система векторов называется линейно зависимой, если существуют числа , не равные одновременно нулю, такие что =

Если это равенство для данной системы векторов возможно лишь при , то эта система векторов называется линейно независимо.

6)Базис n-мерного пространства.Разложение вектора по базису. Максимально независимая подсистема системы векторов называется ее базисом.

Линейная комбинация называется разложением вектора по векторам , а числа называются коэффициентами этого разложения.

7)Определители и их свойства. Вычисление определителя 3-го порядка по методу треугольника. Любой квадратной таблице чисел размером nхn ставится в соответствие по определенному закону некоторое число, называемое определителем n-го порядка. Обозначение определителя илиОсновные свойства определителей:

1⁰. При транспонировании матрицы определитель не меняется.

2⁰. При перестановке двух строк (столбцов) определитель меняет знак на противоположный.

3⁰. Общий множитель элементов любой строки (столбца) можно вынести за знак определителя.

4⁰. Если некоторая строка или столбец определителя состоит из нулей, то определитель равен нулю.

5⁰. Определитель равен нулю, если элементы каких-нибудь двух строк (столбцов) его пропорциональны.

6⁰. Если определитель содержит одинаковые строки (столбцы), то он равен нулю.

7⁰. Определитель не изменится, если к элементам любой строки (столбца) прибавить соответствующие элементы другой строки (столбца), умноженные на любое число.

8) Миноры и алгебраические дополнения. Вычисление определения разложения по элементам строки или столбца.

Минором М_ij элемента а_ij называется определитель, полученный вычеркиванием i -ой строки и j-го столбца. Алгебраическим дополнением элемента а_ij называется число Определитель равен сумме произведений элементов любой строки (столбца) на их алгебраические дополнения.

.

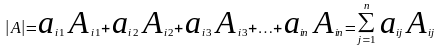9) Матрица и ее разновидности прямоугольная, квадратная, диагональная,единичная,нулевая,транспонирования,присоединенная.Матрицей называется упорядоченная таблица чисел. (А_{m x n}) m-число строк, n –число столбцов. Числа стоящие в матрице называются ее элементами. Виды матриц:

Квадратная матрица- матрица у кот. число строк равно числу столбцов. Н:

Матрица строка состоит из одной строки.

Матрица столбец состоит из одного столбца.

Диагональная матрица- квадратная матрица все элементы кот. кроме диагональных =0.

Диагональные элементы- элементы у кот. номер строки = номеру столбца:

Единичная матрица- диагональная матрица у кот. диагональные элементы =1

Транспонированием матрицы называется замена строк матрицы на ее столбцы с сохранением их порядка.