Параметри і числові характеристики неперервних законів розподілу

Нехай випадкова величина Т вимірюється або спостерігається кілька разів. Припустимо, що t набуває дискретних значень. Їх розглядають як реалізацію випадкової величини Т. Випадкові події утворюють розподіл, який повністю описується функцією щільності розподілу f(t) та інтегральною функцією розподілу F(t).

Функція щільності розподілу (інакше диференціальний закон розподілу) f(t) – це відносна частота появи значення t. Вона показує імовірність, з якою з’являється певне значення t. Інтегральна функція розподілу F(t) показує імовірність того, що випадкова величина Т є менша або дорівнює аргументу t:

Інтегральна функція розподілу монотонно збільшується, поки не досягне значення 1.

Функція щільності розподілу – це похідна від інтегральної функції розподілу, а інтеграл від функції щільності розподілу ймовірностей є інтегральною функцією:

Імовірність того, що неперервна величина точно набуває значення t, дорівнює нулю.

Дискретний розподіл найбільше виявляється тоді, коли значення згруповані та впорядковані за різноманітними класами. Як правило, сукупність N значень ознак рекомендується впорядковувати по √ N класів. На відміну, при неперервному розподілі випадкова змінна Т набуває будь-яких значень t.

Наведемо приклади деяких неперервних законів розподілу.

Рівномірний розподіл (інакше прямокутний) має широке застосування у математичній статистиці. Його використовують для опису випадкових величин, значення яких лежать у межах визначеного інтервалу і які мають однакову імовірність. Щільність розподілу f(t) постійна у деякому інтервалі (a, b) і дорівнює нулю поза його межами:

Інтегральна функція розподілу F(t) має вигляд:

Математичне очікування рівномірного розподілу

середнє квадратичне відхилення

Закон розподілу однопараметричний: це границі зміни випадкової величини (a, b).

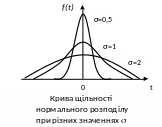
Нормальний розподіл (розподіл Гаусса) застосовують, коли випадкова
величина є результатом дії значного числа факторів за умови, що всі фактори мають однаково незначний вплив. Аргумент t розподілу Гаусса - це неперервна змінна. Закон двопараметричний: a - математичне очікування випадкової величини, центр розсіювання, характеризує положення розподілу на осі абсцис;  - середнє квадратичне відхилення СКВ, характеризує форму розподілу.

Функція щільності розподілу f(t) імовірності та інтегральна функція розподілу F(t) мають вигляд:

Нормальний розподіл описує неперервні розподіли, для яких площа під кривою щільності розподілу завжди дорівнює одиниці.

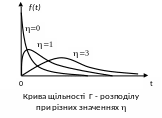
Гамма-розподіл описує час, необхідний для появи рівно  незалежних
подій, якщо вони відбуваються з постійною інтенсивністю . Розподіл 2-параметричний:  - параметр форми,  - параметр масштабу. Числові характеристики: математичне очікування і дисперсія: Гамма-розподіл характеризується щільністю імовірності

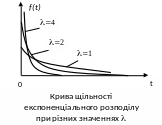
Експоненціальний розподіл – окремий випадок Г- розподілу при =1.
Описує час до появи однієї події, якщо події відбуваються з постійною інтенсивністю . Закон розподілу однопараметричний: параметр =а-1; числові характеристики а==-1. Функція щільності експоненціального (інакше показникового) розподілу

Параметри і числові характеристики дискретних законів розподілу

Наведемо стислі характеристики деяких дискретних законів розподілу.

Розподіл Пуассона – граничний випадок біноміального розподілу.
При найпростішому потоці число подій на фіксованому проміжку часу розподілено за законом Пуассона: Це імовірність того, що за час t відбудеться рівно х подій. При цьому інтервали між подіями розподілено за експоненціальним законом:

Існують розрахункові таблиці для значень функції f(t) для різних х при різних a=t. Параметр  - це щільність вхідного потоку подій та числова характеристика розподілу Пуассона a=t.

Особливість закону Пуассона: дисперсія випадкової величини дорівнює її математичному очікуванню. Цю властивість часто застосовують на практиці при перевірці гіпотези про пуассонівський розподіл.

Біноміальний розподіл описує результат експерименту, при якому можуть з’явитися лише дві події, що взаємно виключають одна одну, тобто можливі лише два наслідки: успіх і невдача. Функція щільності розподілу P(m) визначає імовірність m успіхів при n експериментах (випробуваннях, замірах), а інтегральна функція розподілу F(m) виражається як сума комбінацій з n по m:

де n - число замірів; m - число успішних замірів; p - імовірність успіху;

(1-p) - імовірність невдачі; (1-p)=q.

Параметр розподілу p і числові характеристики – математичне очікування а та дисперсія D – визначаються наступним чином:

При p=0,5 (тобто успіх і невдача рівноімовірні) розподіл симетричний і може бути апроксимований нормальним.

Геометричний розподіл описує результат експерименту, в якому при m замірах після (m-1) невдалих замірів з’являється вдалий наслідок з імовірністю

Параметр розподілу p і числова характеристика – математичне очікування а– визначаються наступним чином: