3.8. Розкриття деяких невизначеностей

Як бачимо з прикладу 5.5, у найпростіших випадках знаходження границі зводиться до підстановки у функцію граничного значення аргументу . Але часто така підстановка приводить до невизначених виразів. Це такого типу вирази:

1. відношення двох нескінченно малих величин – невизначеність вигляду ;

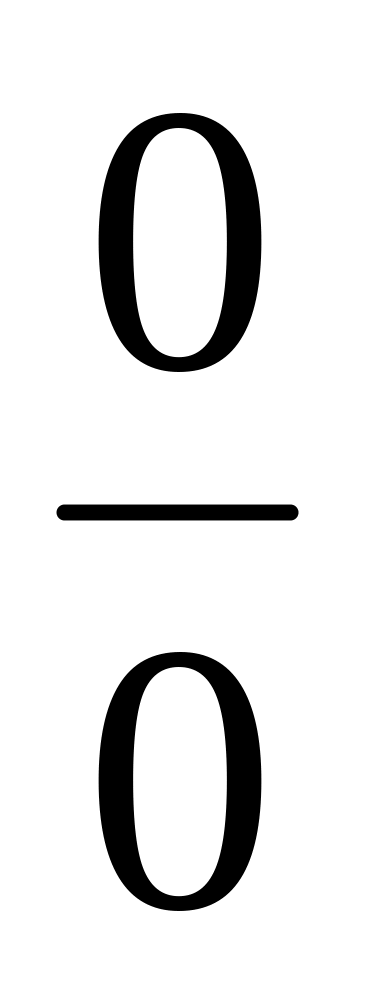2. відношення двох нескінченно великих величин – невизначеність вигляду ;

3. різниця двох нескінченно великих величин – невизначеність вигляду та інші.

Операцію знаходження границі у цих випадках називають розкриттям невизначеності.

Розглянемо деякі окремі випадки.

1. Невизначеність вигляду , задана відношенням двох многочленів

Приклад 5.7. Знайти .

Розв’язування. Маємо:

границя чисельника ,

границя знаменника ,

тому застосувати теорему про границю частки не можна, оскільки маємо невизначеність . Щоб розкрити дану невизначеність, застосуємо загальний прийом; розкладемо чисельник і знаменник на множники, серед яких обов’язково буде множник :

, .

Підставивши, одержані розклади в границю дістанемо

.

Скорочення на ( ) можливе, тому що при визначені границі значення (у даному прикладі ).

Множник , через який чисельник і знаменний прямують до нуля, інколи називають критичним множником.

Узагальненням даного випадку є відшукання границі дробово-раціональної функції , коли граничне значення аргументу є коренем чисельника і знаменника кратності k.

Виділивши у чисельнику і знаменнику множник , дістанемо

.

Оскільки многочлени і не мають спільних множників, то границя знаходиться підстановкою значення в одержаний вираз дробово-раціональної функції.

2. Невизначеність вигляду , задана ірраціональними виразами

Приклад 5.8. Знайти .

Розв’язування. При маємо невизначеність , отже – критичний множник. Позбудемося ірраціональності в чисельнику. Помножимо чисельник і знаменник на спряжений вираз до чисельника. Маємо

.

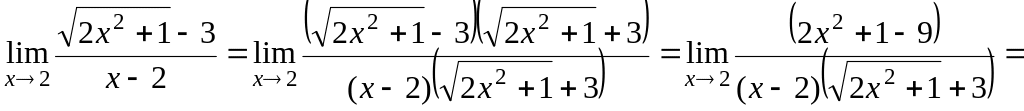
3. Невизначеність вигляду , задана відношенням двох многочленів

Нехай потрібно знайти границю дробово-раціональної функції

.

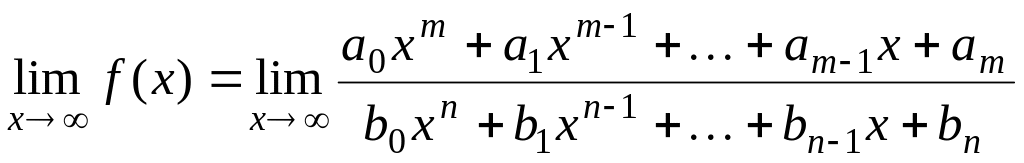Розглянемо такі випадки:

1) Нехай , тоді, розділивши чисельник і знаменник на , знаходимо

.

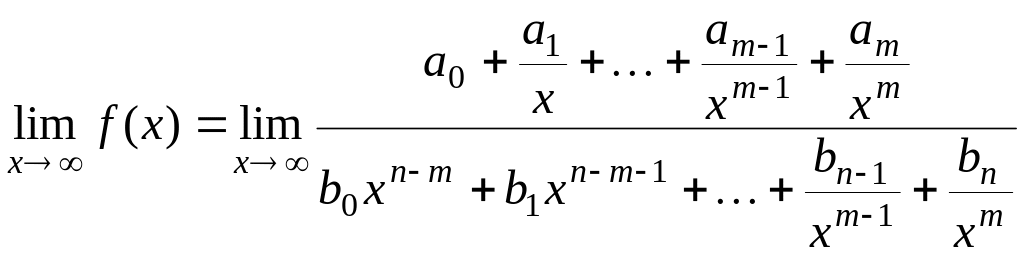Якщо тепер перейти до границі у кожному доданку чисельника і знаменника, то у чисельнику дістанемо число , а у знаменнику – нескінченність. Відношення скінченого числа до нескінченної величини є нескінченно мала величина, тобто .

2) Нехай , тоді, розділивши чисельник і знаменник на , дістанемо

.

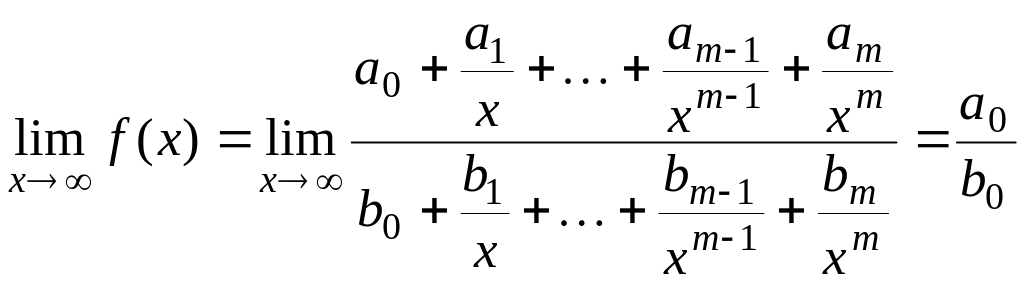3) Нехай , тоді, розділивши чисельник і знаменник на , знаходимо

.

Якщо тепер перейти до границі у кожному доданку чисельника і знаменника, то у чисельнику дістанемо нескінченність, а у знаменнику – число . Таке відношення дає нескінченно велику величину, тобто . Отже,

.

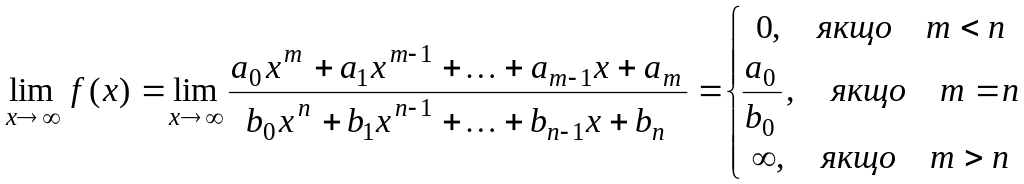Приклад 5.9. Знайти .

Розв’язування. Маємо невизначеність . Поділимо чисельник і знаменник дробу на .

.

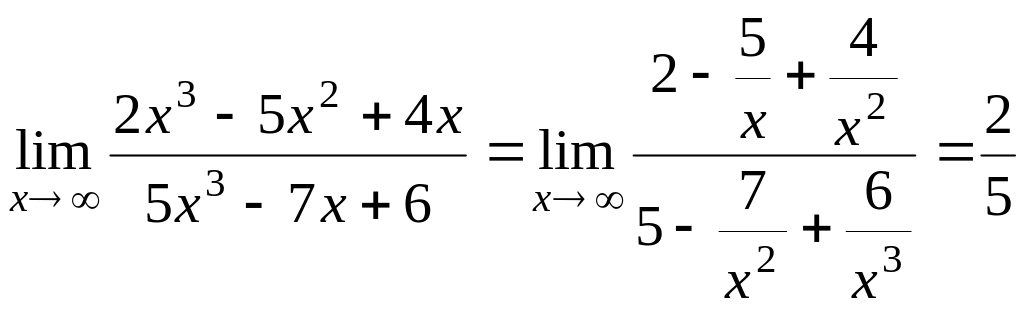3.9. Дві важливі (чудові) границі Перша важлива границя: .

Доведення. Функція визначена в області . Оскільки має місце рівність , то функція парна, з чого випливає, що вона симетрична відносно осі ординат. Тому, якщо в точці існують однобічні границі, то вони рівні між собою, тобто:

Рис. 5.16

Розглянемо границю цієї функції в точці справа і доведемо, що .

Побудуємо у першій чверті координатної площини коло одиничного радіуса (рис. 5.16) і візьмемо кут х , який дорівнює аргументу функції.

Тоді:

1) ; 2) ;

3) .

Порівнюючи площі трикутників ОАС, ОВС і кругового сектора ОАС, маємо

, звідки

.

Розділивши останні нерівності на , дістанемо

або .

Оскільки , то згідно теореми Гур’єва, маємо .

Приклад 5.10. Знайти границю функції , при .

Розв’язування. Зведемо дану границю до першої важливої границі, помноживши та поділивши дріб на а, і ввівши позначення :

.

Друга важлива границя , .

Доведено, що е – ірраціональне число і не є коренем ніякого алгебраїчного рівняння з цілими коефіцієнтами. Його наближене значення з точністю до дорівнює 2,718281828459045. Логарифми чисел за основою е називаються натуральними і позначаються .

При обчисленні границь, пов’язаних з числом е, часто застосовують таке твердження: якщо існують границі і , причому , то існує також границя , яка обчислюється за формулою

.

Приклад 5.11. Знайти границю функції .

Розв’язування. Зведемо дану границю до другої важливої границі:

.
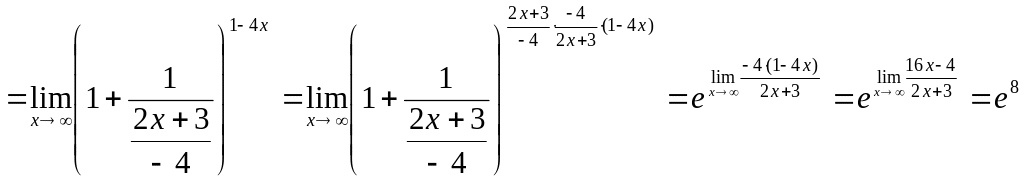