§ 3. Границя функції

3.1. Числова послідовність

В попередньому параграфі ми розглядали функції, областю визначення яких були числові проміжки. Такі функції називають функціями неперервного аргументу. Ці функції найчастіше використовуються для характеристики різних фізичних процесів.

Разом з тим, на практиці часто застосовуються функції, задані на множині натуральних чисел, тобто функції вигляду , де . Відомо, наприклад, що сума внутрішніх кутів -кутника в радіанах визначається формулою , отже є функцією натурального аргументу.

Означення 1. Числовою послідовністю називається числова функція , аргумент якої належить множині натуральних чисел .

Якщо ― натуральне число, ― значення послідовності в точці , то кажуть, що ― номер числа , а саме число називається -м членом послідовності. Часто замість пишуть або .

Приклад 5.2. Написати перші чотири члени послідовності , якщо:

1) ; 2) , .

Розв’язування. 1) Підставляючи почергово в формулу для загального члена послідовності, знаходимо: , , , .

2) У відповідністю з формулою маємо: , , .

Означення 2. Число називають границею послідовності , якщо для довільного, як завгодно малого, числа існує такий номер , що для всіх , , виконується нерівність .

Якщо це виконується, то пишуть і кажуть, що послідовність , має границю і є збіжною.

Приклад 5.3. На основі означення довести, що границя послідовності дорівнює 1.

Розв’язування. Позначимо і виберемо довільне число . Тоді для вибраного знайдеться номер , що для виконується нерівність .

Нехай . Тоді і нерівність буде виконуватись для . Знайшли , починаючи з якого нерівність виконується. Якщо . Тоді . Отже нерівність буде виконуватись для звідки . Одержані результати підтверджують, що задана послідовність має границю 1, тобто .

3.2. Границя змінної величини

Стале число є границею змінної величини , якщо для кожного наперед заданого довільно малого числа можна вказати таке значення змінної , що всі наступні значення змінної будуть задовольняти нерівність .

Якщо число є границею змінної величини , то кажуть, що прямує до границі , і пишуть або .

Якщо порівняти означення границі послідовності й границі змінної, то в означенні границі послідовності йдеться про номер того члена послідовності , починаючи з якого виконується нерівність , а в означенні границі змінної йдеться про числове значення цієї змінної, починаючи з якого виконується нерівність .

3.3. Границя функції в точці

Нехай функція задана в деякому околі точки , крім, можливо, самої точки _.

О

Рис. 5.10

значення 3. Число b називається границею функції при x, що прямує до (або в точці ), якщо для будь-якого (як завгодно малого), знайдеться таке додатне число , що для всіх х, таких, що виконується нерівність .

Коротко це означення записують так .

В подальшому, для скорочення записів, будемо вживати три найпростіші символи або квантори:

― означає "для будь-якого", "для всякого"; ― означає "існує", "знайдеться"; ― означає "виконується", "слідує".

Тоді на мові кванторів означення границі запишеться так:

.

На рис. 5.10 показано геометричну інтерпретацію границі функції в точці: число b є границею функції при , якщо для довільного ε-околу точки b знайдеться δ- окіл точки , такий, що коли значення аргументу х взяти з множини , то відповідні значення функції лежатимуть в ε-околі точки b.

Приклад  5.4. Довести, що .

Розв’язування. Згідно означення границі, маємо:

.

З останньої нерівності випливає, що . Для того, щоб виконувалась остання нерівність достатньо взяти .

Зауваження. Якщо функція має границю число , лише при умові, що зліва, то використовується запис: , а число називається однобічною границею функції зліва.

Якщо функція має границю при справа, то використовується запис .

Для існування границі функції в точці необхідно і достатньо, щоб .

Рис. 5.11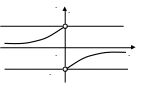

Якщо в деякій точці лівостороння границя функції не дорівнює правосторонній, то функція має розрив в цій точці.

Наприклад, функція в точці має різні односторонні границі: .