3.3. Погрешности потенциометрических преобразователей.

1. Абсолютная погрешность.

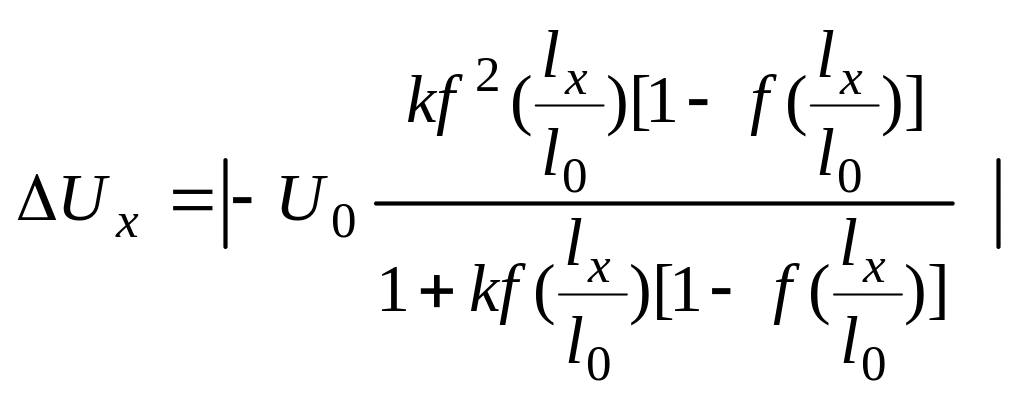(5.12)

Рис. 5.5. Зависимость абсолютной погрешности от положения ползунка потенциометрического преобразователя при различных значениях коэффициента нагрузки.

2. Относительная погрешность.

С учетом вышеприведенных выражений получим

(5.13)

Рис. 5.6. Зависимость относительной погрешности от положения ползунка потенциометрического преобразователя при различных значениях коэффициента нагрузки.

3. Приведенная погрешность.

с учетом того, что U_max=U₀ получим следующее выражение.

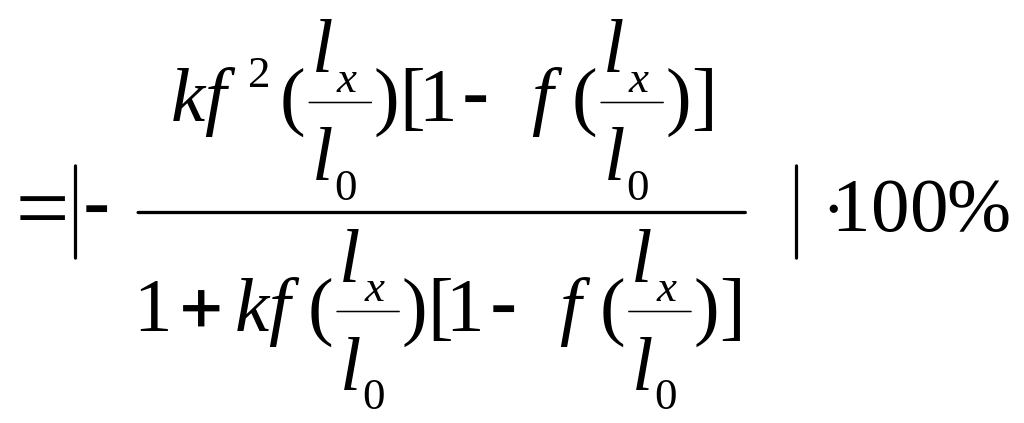(5.14)

Рис. 5.7. Зависимость приведенной погрешности от положения ползунка потенциометрического преобразователя.

Из анализа работы потенциометрических преобразователей следует, что если требуются строго линейные характеристики, сопротивление нагрузки R_н выбирается в десятки раз больше, чем сопротивление потенциометрического преобразователя.

Приведенные выше потенциометрические преобразователи являются нереверсивными, так как при любом положении ползунка знак выходного напряжения или его фаза не меняются.

Различные варианты двухтактных (реверсивных) схем включения потенциометров представлены на рис. 5.8.

Возможность уравновешивания схемы с помощью ползунка делает ненужным применение постоянных сопротивлений в дифференциальной схеме (рис. 5.8, а) и мостовой схеме с двумя потенциометрами (рис. 5.8, б). Возможность осуществления второго (постоянного) контакта с витками потенциометра приводит к предельно простой реверсивной схеме (рис. 5.8, в).

Заметим, что в варианте с двумя потенциометрами лучшие результаты дает схема, изображенная на рис. 5.8, г с двумя дополнительными соединенными между собой постоянными контактами.

Рис. 5.8. Реверсивные схемы включения потенциометров и их передаточные характеристики: а, д – дифференциальная; б, е – мостовая с двумя потенциометрами; в, ж – простейшая; г, з – мостовая с двумя потенциометрами со средней точкой.

Это объясняется тем, что при нулевом положении ползунка выходные сопротивления этих схем равны нулю и поэтому для малых отклонений ползунка они дают линейную статическую характеристику, мало зависящую от величины нагрузки. По той же причине эти схемы дают и более высокий КПД.

Основным недостатком потенциометрических датчиков является наличие скользящего контакта, снижающего надежность работы. Достоинство потенциометров заключаются в конструктивной простоте, небольших габаритах и весе, а так же в возможности питания как постоянным, так и переменным током.

4. Расчет потенциометрических датчиков.

При расчете потенциометрических датчиков применительно к условиям их работы в системах автоматического регулирования обычно требуется определить статическую характеристику и температуру обмотки.

Найдём уравнение статической характеристики U_вых=f(x_вх) для схемы, приведенной на рис. 5.8, в, полагая, что потенциометр является линейным, т.е. все его витки имеют одинаковую длину.

Составим эквивалентную схему (рис. 5.9) и определим общее сопротивление цепи r_э относительно входных зажимов, обозначив полное сопротивление самого потенциометра r₀ :

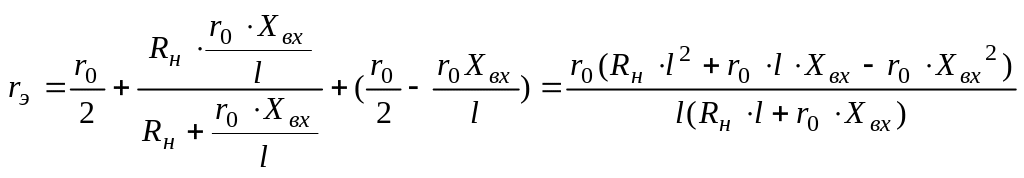
Отсюда общий ток цепи

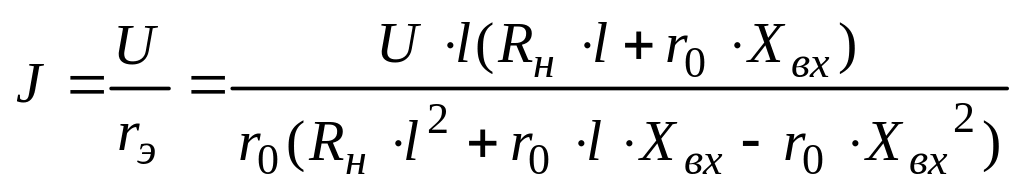(5.15)

а выходное напряжение в предположении, что источник, питающий цепь, обладает нулевым внутренним сопротивлением,

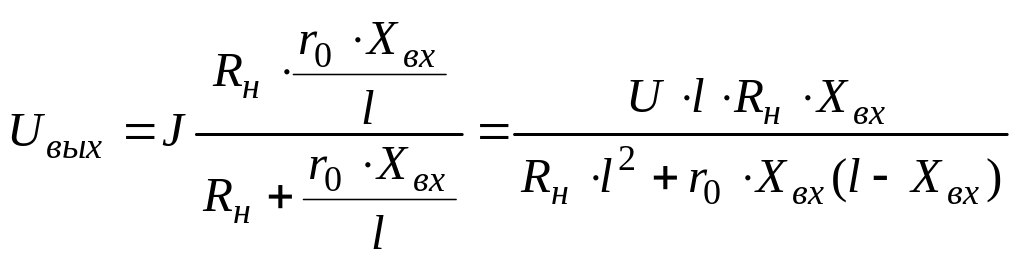(5.16)

Зависимость U_вых=f(X_вх) изображена на рис. 5.10 (кривая 2).

При Х_вх=Х_{вх max}=

(5.17)

Представив выражение (5.17) в виде

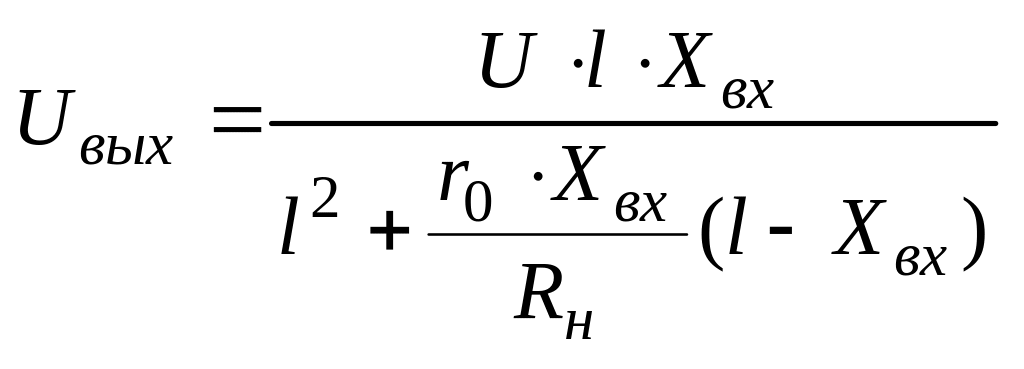
заметим, что при соблюдении условия R_н>>r₀ второй член знаменателя будет значительно меньше первого и им можно пренебречь. В этом случае выражение (5.16) приводится к виду:

(5.18)

и зависимость U^I_вых=f(X_вх) есть прямая, проведенная из начала координат под углом (кривая 1). Практически выражение (5.18) дает достаточно точные результаты уже при соотношении R_н>(8…10)r₀

В некоторых случаях, когда вероятные отклонения ползунка в процессе работы системы автоматического регулирования достаточно велики, большую точность может дать линеаризация статистической характеристики методом секущей. Секущая 3 проводится из начала координат в точку А^I с координатами (Х_{вх max} U^I_{вых max}), соответствующую наиболее вероятному максимальному отклонению ползунка. В этом случае

Рис 5.9. Эквивалентная схема потенциометра, включенного по схеме изображенной на рис. 5.8, в.

Рис. 5.10. Статистические характеристики линейного потенциометра включенного по схеме, показанной на рис. 5.8, в.

1 – нагруженный потенциометр; 2 – потенциометр с нагрузкой;

3 – линеаризованная характеристика нагруженного потенциометра.

где 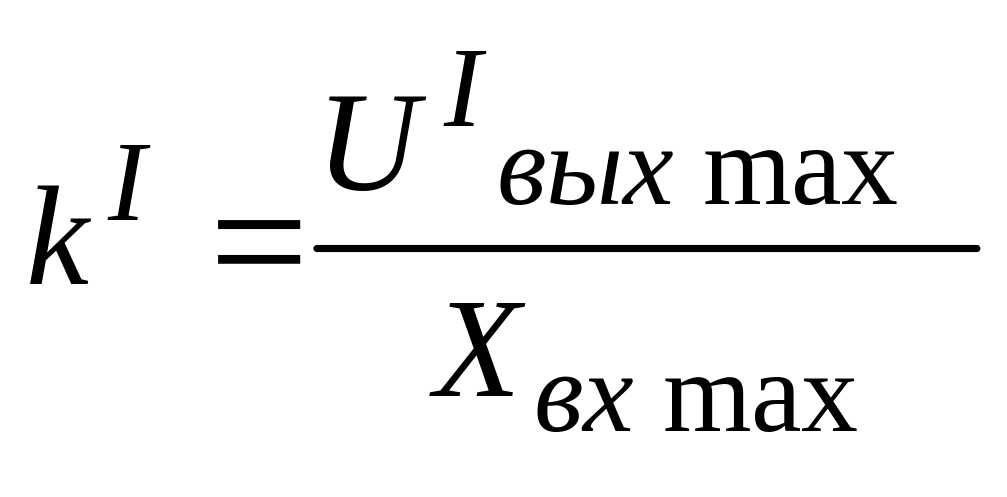(5.19)

Предполагая, что ток нагрузки достаточно мал, а температурный коэффициент сопротивления провода незначителен, перегрев обмотки можно найти из уравнения теплового баланса

(5.20)

где S – площадь поверхности резистора;

- коэффициент теплоотдачи;

- перегрев обмотки;

r₀ – сопротивление обмотки;

в – коэффициент рассеяния.

При выборе допустимой температуры обмотки потенциометра этот вопрос необходимо рассмотреть с двух точек зрения: работы скользящего контакта и возникающих в обмотке механических напряжений.

Желательно, чтобы температура контактных поверхностей не превышала 200⁰ С, так как при более высоких температурах для многих материалов начинается интенсивное окисление.

Надежное контактирование можно обеспечить только в результате правильного выбора натяжения проволоки в процессе намотки. Для этого, помимо конструктивных данных потенциометра, необходимо знать минимально и максимально возможную температуру его обмотки и каркаса.

Для определения конструктивных размеров потенциометра рекомендуется следующая последовательность расчета, которая будет дана для тороидальной конструкции каркаса (см. рис. 5.11), включенного по схеме, приведенной на рис. 5.8, в.

Будем полагать, что заданы:

максимальная величина входного перемещения в одну сторону α_вх.max (рад), чувствительность К; допустимый входной момент М_вх; величина сопротивления нагрузки R_н.

Рис. 5.11. Устройство потенциометра с тороидальным каркасом.

1 – каркас; 2 – обмотки; 3 – ползунок

Предположим, что условие R_н>>r₀ может быть выдержано. Требуемая величина питающего напряжения определяется из выражения:

или с учетом запаса по перемещению (порядка 1,3…1,8)

U=3Kα_{вх max} (5.21)

Далее, задавшись материалом обмотки и контактирующей части ползунка, из соотношения

M_вх=RF_n=RFμ (5.22)

можно выбрать радиус потенциометра R и величину контактного давления F.

Здесь μ – коэффициент трения контактирующих поверхностей; F_n – усилие требуемое для перемещения ползунка.

Выбор радиуса потенциометра определяет и длину дуги каркаса (см. рис.5. 10).

(5.23)

Если далее задаться допустимым перегревом обмотки , то высота каркаса h и его толщина b определяются выбором диаметра провода обмотки d.

Действительно, учитывая, что в первом приближении

S=2(h+b) ,

а так же что

(5.24)

где - удельное сопротивление;

q – площадь поперечного сечения провода

На основании выражения (20) будем иметь.

Отсюда

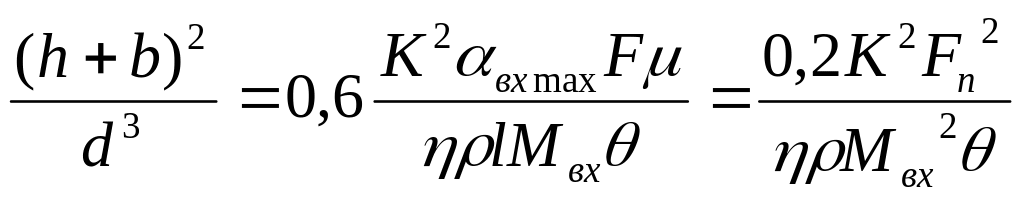(5.25)

Уменьшение диаметра проволоки желательно как с точки зрения уменьшения размеров потенциометра, таки с точки зрения уменьшения ступенчатости статической характеристики (для снижения шумов в системе автоматического регулирования). Однако при этом необходимо ориентироваться на механическую прочность проволоки и, в частности, проверить возникающие в ней напряжения температурного характера.