
- •В каких случаях в триангуляционной сети возникает геометрическое условие координат. Привести примеры.
- •Вывести формулу сферического избытка треугольника, используя формулу Лежандра.
- •Задача 1 Редуцирование треугольника триангуляции 1 класса с эллипсоида Красовского на плоскость в проекции Гаусса — Крюгера и вычисление прямоугольных координат его вершин.
- •Задача 2 Параметрическое уравнивание нивелирной сети.
- •Задача 3 Уравнивание нивелирной сети способом красных чисел ( Попова в.В.)
- •Задача 4 Уравнивание линейно-угловой сети методом последовательных приближений
Задача 1 Редуцирование треугольника триангуляции 1 класса с эллипсоида Красовского на плоскость в проекции Гаусса — Крюгера и вычисление прямоугольных координат его вершин.
Дано:
B=58034’32.299”
L=104005’07,087”
1 = 77°39’23.13”
2 = 47°35’53.88”
3 = 54°44’45.93”
S1-2 = 36312.27
A1-2 = 300°39’15.38”
1 04005’07,087”
: 6 = 18 (номер
зоны)
04005’07,087”
: 6 = 18 (номер
зоны)
L0 = 6*18 – 3 = 105º
l° = L – L0 = - 0º54’52.48”
l
=
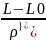 =
-0°0’0.02”
=
-0°0’0.02”
где
 = 206264.806”
= 206264.806”
широту полностью переводим в секунды
В” = (58º*3600) + (34*3600) +32.299 = 210872.299
Формулы:
x=6367558,4969 B”/p”-{a0-[0,5+(a4+a6*l2)l2 ] l2*N}*SinB*CosB
y=[1+(a3+a5* l2) l2]l*N*CosB
N=6399698,902-[21562,267-(108,973-0,612*Cos2B) *Cos2B] *Cos2B
a0=32140,404-[135,3302-(0,7092-0,0040*Cos2B) *Cos2B] *Cos2B
a4=(0,25+0,00252*Cos2B) *Cos2B-0,04166
a6=(0,166*Cos2B-0,084) *Cos2B
a3=(0,3333333+0,001123*Cos2B) *Cos2B-0,1666667
a5=0,0083-[0,1667-(0,1968+0,0040*Cos2B) *Cos2B] *Cos2B
№ действия |
Формулы |
Результат |
1 |
B0 |
58034’32.299” |
2 |
B” |
210872.299 |
3 |
B”/p” |
1,022337756 |
4 |
SinB |
0.853329193 |
5 |
CosB |
0.521372503 |
6 |
Cos2B |
0.271829286 |
7 |
l0=L-L0 |
-0054’52,48” |
8 |
l” |
-3292,48” |
9 |
l=l”/p” |
-0.015962393 |
10 |
N |
6393845,686 |
11 |
a0 |
32103,66961 |
12 |
a4 |
0.026483527 |
13 |
a6 |
-0.010567727 |
14 |
a3 |
-0.075973967 |
15 |
a5 |
-0.022391818 |
16 |
SinB*CosB |
0.444902377 |
17 |
l2 |
0.0002547979 |
18 |
N*l2 |
1629.139031 |
19 |
6367558,4969B”/p” |
6509795.465 |
20 |
x |
6495874.875 |
21 |
1+(a3+a5* l2) l2 |
0.99998064 |
22 |
[21]*l*CosB |
-0.008322192 |
23 |
y |
-53210.809 |
X1 = 6495874.875
Y1 = -53210.809
Вычисляем
сближения меридиана «
 1»
в
исходной точке 1 по формуле.
1»
в
исходной точке 1 по формуле.
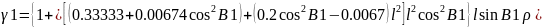 =
-0°46’49.63”
=
-0°46’49.63”
Вычислим приближенное значение дирекционного угла исходной стороны
 =
301º26’5.01”
=
301º26’5.01”
1

2 3
Далее вычисляем приближенные значения сторон по теореме синусов
S2-3 = S1-2 *sin1: sin3 = 48037,855
S1-3 = S1-2 *sin2: sin3 = 32836,384
Вычисляем приближенные значения координат
X2
=
X1
+ S1-2*cos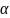 1-2
= 6514812,699 X3
=
X1
+ S1-3*cos
1-3
= 6472166,264
1-2
= 6514812,699 X3
=
X1
+ S1-3*cos
1-3
= 6472166,264
Y2 = Y1 + S1-2*sin 1-2 = -84193,704 Y3 = Y1 + S1-3*sin 1-3 = -75929,301
Где 1-3 = 1-2 - 1 = 223º46’41.8”
Вычислим поправки за кривизну геодезических линий по формулам
 =
3,04
=
3,04
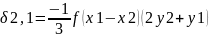 =
-3,54
=
-3,54
где f = 0,00253
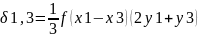 =
-3,64
=
-3,64
 =
4,10
=
4,10
 =
-8,79
=
-8,79
 =
8,49
=
8,49
Вычислим поправки в углы за кривизну геодезических линий
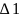 =
=
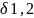 –
–
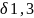 =
6,68
=
6,68
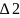 =
=
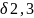 –
–
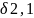 =
- 5,24
=
- 5,24
 =
=
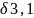 –
–
 =
- 4,39
=
- 4,39
Находим углы треугольника на плоскости
1пл = 1изм + = 77º39’29.81”
2пл = 2изм + = 47º35’48.64”
3пл = 3изм + = 54º44’41.54”
Вычислим дирекционные углы направлений
1-2
=
 1-2
+
=
301°26’8.05”
1-2
+
=
301°26’8.05”
1-3 = 1-2 - 1пл = 223º46’38.24”
2-3 = 1-2 + 2пл - 180º = 169º01’56.69”
Редуцируем исходную формулу на плоскость в проекции Гаусса по формуле

S1-2пл = 36314,417
Вычисляем другие стороны плоского треугольника по теореме синусов
S2-3пл = S1-2 *sin1 пл: sin3 пл = 48042,150
S1-3пл = S1-2 *sin2 пл: sin3 пл = 32838,058
Находим координаты пунктов «2»и «3»
X2 = X1 + S1-2*cos 1-2 = 6514814,275 X3 = X1 + S1-3*cos 1-3 = 6472164,663
Y2 = Y1 + S1-2*sin 1-2 = -84195,257 Y3 = Y1 + S1-3*sin 1-3 = -75930,050
