НОУ СПО «Волгоградский колледж газа и нефти» ОАО «ГАЗПРОМ»

Факультет «Автоматика и вычислительная техника»

Методические указания

по дисциплине

«Компьютерное моделирование»

для студентов базового уровня подготовки

СПЕЦИАЛЬНОСТЬ 220703

Лабораторная работа №1 «Матричные вычисления. Решение систем линейных уравнений»

Волгоград 2012

Рассмотрены и одобрены на заседании цикловой комиссии «Комиссия автоматизированных систем управления, вычислительной техники и прикладной математики»: Протокол №____ от «___»__________200__г.
Составитель: к.ф.-м.н., доцент Казаков Н.В. –старший преподаватель специальных дисциплин ВКГН

Содержание

«Матричные вычисления. 1

Решение систем линейных уравнений» 1

1. Цель работы: научиться проводить матричные операции и решать системы линейных алгебраических уравнений путем написания специализированных программ на языке высокого уровня. 4

6. Рекомендуемая литература 15

1. Цель работы: научиться проводить матричные операции и решать системы линейных алгебраических уравнений путем написания специализированных программ на языке высокого уровня.

2.Краткие теоретические сведения.

Системы из n линейных уравнений вида (1) решаются точными и итерационными методами. Точные методы дают точное решение за конечное число операций, если вычисления по ним выполнялись без погрешности. Число операций у итерационных методов непостоянно и зависит от заданной погрешности вычислений.

	a11x1	+	a12x2	+	...	+	a1nxn	=	b1
	a21x1	+	a22x2	+	...	+	a2nxn	=	b2
	...	...	...		...	...	...	...	...		(1)

	an1x1	+	an2x2	+	...	+	annxn	=	bn

Метод Гаусса последовательного исключения неизвестных ( предложен в 1849). Способ относится к точным методам. Простейший метод основан на приведении матрицы коэффициентов a_ij к треугольному виду (прямой ход) и дальнейшем последовательном определении переменных x_n,x_n-1,...,x₁ (обратный ход). При этом реализуется следующий алгоритм. Разделим первое уравнение на a₁₁ и приведем его к виду x₁+a₁₂⁽¹⁾x₂+...+a_1n⁽¹⁾x_n=b₁⁽¹⁾. Исключим теперь х₁ из остальных уравнений системы. Для этого последовательно умножаем первое уравнение системы на a₂₁,a₃₁,...,a_n1 и вычитаем его из второго, третьего и т.д. уравнения системы. Эти уравнения содержат теперь на одну переменную (x₁) меньше и образуют систему из n-1 уравнения. К этой системе также применяется такое же преобразование и из n-2 уравнений исключается переменная x₂. В итоге за n шагов приходим к системе (2):

	x1	+	a12(1) x2	+	..	+	a1n (1) xn	=	b1(1)
			x2	+	..	+	a2n (2) xn	=	b2(2)
	...	...	...		..	..	...	...	...	(2)

							xn	=	bn(n)

На этом заканчивается прямой ход. Осуществляя обратный ход, подставляем известное из последнего уравнения значение x_n в предпоследнее и находим x_n-1. Затем полученные значения двух неизвестных подставляют в третье с конца уравнение и т.д. В результате получаются все значения неизвестных.

Однако, если коэффициенты a_ij малы (близки к 0), то на k-ом шаге k-ая строка умножается на большое число 1/a_kk^(k) , что приводит к значительным ошибкам округления и даже может вызвать аварийный останов ЭВМ от переполнения. Кроме того, сильно ухудшается точность решения из-за конечной длины машинного счета. Это является существенным недостатком простейшей реализации метода Гаусса.

Метод Гаусса с выбором главного элемента заключается в том, что перед началом решения производится выбор наибольшего по модулю коэффициента в строке, столбце или во всей матрице. Наиболее часто применяется выбор главного элемента по всей матрице и осуществляется перестановка строк и столбцов так, чтобы этот элемент оказался в верхнем левом углу матрицы коэффициентов. После чего производится счет по ранее рассмотренному алгоритму. Этот способ повышает точность решения при наличии ошибок округления. Для правильности расчетов на ЭВМ с числами с плавающей запятой достаточен выбор A(i,i)0.

Метод вращения является разновидностью метода Гаусса обладающей повышенной устойчивостью к погрешностям промежуточных вычислений и заключается в преобразовании системы координат, приводящем исходную матрицу коэффициентов к треугольному виду. Он реализуется в следующей последовательности.:

После введения a_ij и b_i вычисляем параметры

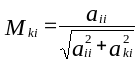и ,

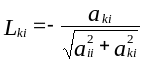причем, если a_ii=a_ki=0, то M_ki=1 и L_ki=0. После чего проводятся преобразования системы по формулам:

M_kiy_i-L_kiy_k=M_kib_i-L_kib_k

L_kiy_i-M_kiy_k=L_kib_i-M_kib_k

где i=1,2,...,n+1, k=i+1,...,n, y_i и y_k - левые части, а b_i и b_k правые части i-го и k-ого уравнений соответственно. После n(n-1)/2 шагов приходим к системе с верхней треугольной матрицей. После чего проводим обратный ход

Метод простых итераций (от латинского iteratio - повторение) или метод последовательных приближений заключается в задании первоначальных значений искомых переменных и последовательном вычислении их всё более точных значений по одним и тем же формулам. Суть метода состоит в реализации итерационного процесса по следующей формуле:

X_i^(k+1)=f_i(X_i^(k)),

применяемой после преобразования системы уравнений общего вида F(X_i)=0 к виду X_i=f_i(X_i). В этих формулах i - номер переменной (1,2,....N), k - номер итерации. Вычисления ведутся до тех пор, пока выполняется условие X_i^(k+1) - X_i^(k)0.

Сходимость метода простых итераций гарантируется, если значения диагональных элементов матрицы коэффициентов превосходят остальные.

Метод Зейделя (предложен в 1874) отличается от метода простых итераций тем, что уточненные X_i(n+1) сразу подставляются в последующие уравнения системы. Обычно это обеспечивает лучшую сходимость. .

Необходимость преобразования вида системы уравнений и трудности с обеспечением быстрой и гарантированной сходимости ограничивают применение методов простых итераций и его модификаций. Однако программная реализация их довольно проста. Кроме того, итерационные методы обладают свойством самоисправления погрешностей вычислений и могут применяться в особых случаях, когда матрица коэффициентов A_ij сильно разрежена (т.е. содержит много нулей) или имеет другие особенности.

Метод минимизации целевой функции заключается в формировании неотрицательной целевой функции вида F(x₁,x₂, ... ,x_n)=f₁ (x₁,x₂,...,x_n)+ f₂ (x₁,x₂,...,x_n)+... f_n (x₁,x₂,...,x_n), компоненты которой формируются из уравнений решаемой системы:

f1(x1,x2,...,xn)	=	a11x1	+	a12x2	+	a1nxn	-	b1
f2(x1,x2,...,xn)	=	a21x1	+	a22x2	+	a2nxn	-	b2
	...	...	...	...	...	...	...	...
fn(x1,x2,...,xn)	=	an1x1	+	an2x2	+	annxn	-	bn

Если x₁,x₂,...,x_n - искомое решение системы линейных уравнений, то функция F(x₁,x₂, ... ,x_n) принимает значение равное нулю (в случае наличия решения) или примет значение, минимизирующее целевую функцию. Целевая функция может быть составлена не только из модулей функций f_i , но и из их квадратов. Подобный подход позволяет решать системы уравнений с переопределенной матрицей. Поскольку, в общем случае число уравнений в системе может быть больше чем число неизвестных, то система может быть несовместной. Её решением в смысле наименьших квадратов считается такой вектор неизвестных, при котором скаляр, определяемый выражением (AX-B)(AX-B) принимает наименьшее значение. Таким образом, решение переопределенной системы сводится к решению новой системы [A^tA][X]=[A^tB], где A^t - транспонированная матрица А. После чего решение может быть проведено любым рассмотренным ранее способом.

Аналогично, приближенное вычисление нормального решения системы линейных уравнений с вырожденной (т.е. определитель которой равен нулю) матрицей осуществляется в предположении, что матрица коэффициентов и матрица свободных членов заданы с некоторым приближением t. Т.е., система уравнений CX=D сводится к системе AX=B, так что c_ij - a_ijt, b_i-d_it. Для решения системы вычисляется параметр =nt. За решение системы принимаются компоненты вектора X_n , получаемые из решения следующей системы [(A^tA+E)][X_n]=[A^tB], где Е -единичная матрица, A^t- транспонированная матрица коэффициентов.