1.3.3 Нестійка аперіодична ланка першого порядку

Диференціальне рівняння цієї ланки

(1.49)

відрізняється від рівняння стійкої аперіодичної ланки першого порядку тільки знаком мінус перед вихідною величиною y.

Передавальна функція

. (1.50)

Використовуючи перетворення Лапласа, одержуємо рішення диференціального рівняння (1.49)

. (1.51)

Координати початкових і кінцевих точок графіка зміни вихідної величини будуть: при t = 0; y= 0 і при ; . Отже, при подачі на вхід ланки стрибкоподібної функції х вихідна величина при прагнутиме також нескінченності і перехідний процес буде незатухаючим, значить, така САР буде нестійкою (рисунок 1.12).

Рисунок 1.13 – Амплітудно-фазова характеристика нестійкої аперіодичної ланки першого порядку.

П

а – графік зміни вхідної величини; б- графік зміни вихідної величини.

Рисунок 1.12 – Графік перехідного процесу нестійкої аперіодичної ланки першого порядку.

ідставляючи в рівняння передавальної функції значення , одержуємо після нескладних перетворень рівняння амплітудно-фазової характеристики

.

Початкова точка цієї характеристики при матиме координати на комплексній площині і , а кінцева точка при — координати і . Отже, амплітудно-фазова характеристика нестійкої аперіодичної ланки першого порядку являє собою півколо, розташоване в третьому квадранті комплексної площини, яке проходить через початок координат і спирається своїм діаметром на від’ємну частину дійсної осі (рисунок 1.133).

1.3.4 Стійка коливальна ланка

Стійкою коливальною ланкою називається така ланка, яка при стрибкоподібній зміні величини на вході прагне на виході до нового усталеного значення, здійснюючи відносно нього затухаючі коливання.

Диференціальне рівняння цієї ланки

, (1.52)

де і — постійні часу ланки в сек.

Передавальна функція

. (1.53)

Характеристичний поліном ланки

. (1.54)

Корені цього рівняння

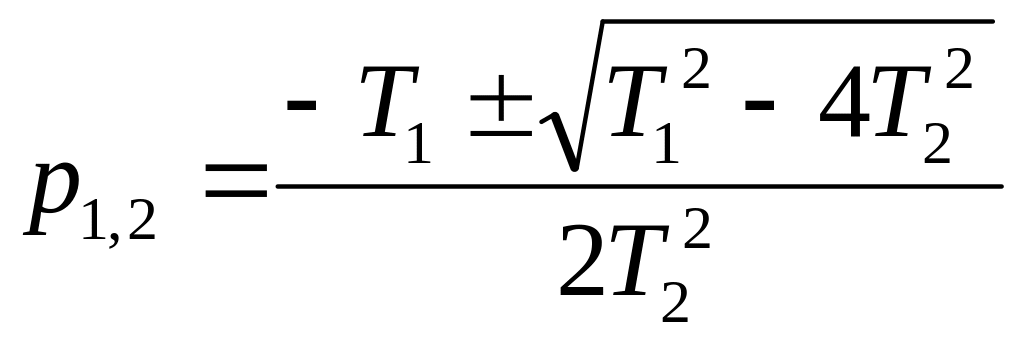. (1.55)

Вираз під коренем, взятий з протилежним знаком, називається дискримінантом

. (1.56)

Розв’язок диференціального рівняння (1.52) в загальному вигляді

. (1.57)

Залежно від величини дискримінанта будуть різні корені характеристичного рівняння (1.54) і, отже, різні розв’язки диференціального рівняння (1.52). При цьому можуть бути три випадки.

1. Дискримінант від’ємний

.

У цьому випадку характеристичне рівняння (1.54) матиме два різних, дійсних і від’ємних кореня.

2. Дискримінант рівний нулю

.

У цьому випадку характеристичне рівняння (1.54) матиме два співпадаючі (кратні) і від’ємні корені.

3. Дискримінант позитивний

.

У цьому випадку характеристичне рівняння (1.54) матиме два спряжені комплексні корені з від’ємними дійсними частинами.

П

а – зміна вхідної величини;

б – зміна вихідної величини.

Рисунок 1.14 – Графік перехідного процесу коливального контуру при D<0.

а – зміна вхідної величини;

б – зміна вихідної величини.

Рисунок 1.15 – Графік перехідного процесу коливального контуру при D=0.

ри від’ємному дискримінанті одержуємо наступне рішення рівняння (1.52):

. (1.58)

Це рівняння показує, що при подачі стрибкоподібного збурення на вхід коливальної ланки у разі D <0 його вихідна величина змінюватиметься по кривій подвійної кривизни і не матиме коливань (рисунок 1.14). Цей випадок має велике значення в практичних дослідженнях, оскільки по кривих такого типу відбувається розгін багатьох технологічних установок.

При дискримінанті рівному нулю одержуємо другий розв’язок рівняння (1.52)

. (1.59)

Це рівняння показує, що при подачі стрибкоподібного збурення на вхід коливальної ланки у разі D = 0 його вихідна величина змінюватиметься по деякій кривій (рисунок 1.19) і не також матиме коливання.

При позитивному дискримінанті одержуємо третє рішення рівняння (1.52)

, (1.60)

де

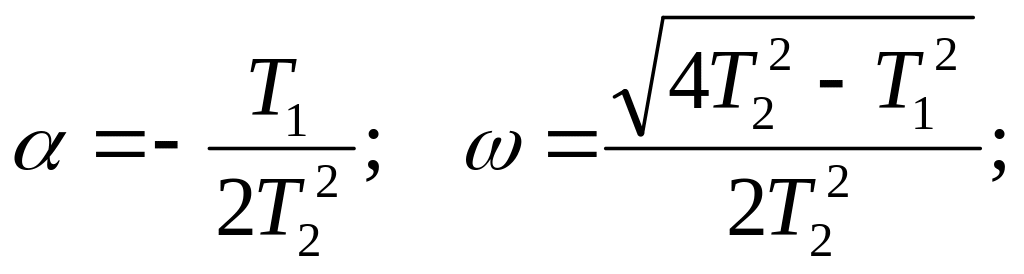
Рівняння (1.60) показує, що при подачі на вхід коливальної ланки стрибкоподібної функції х в разі D > 0 його вихідна величина прагнутиме усталеного значення kx (при ), роблячи при цьому відносно нього затухаючі синусоїдальні коливання із змінною амплітудою (рисунок 1. 16).

О

Рисунок 1.17 – Амплітудно-фазова характеристика коливальної ланки.

тже, тільки у випадку додатного дискримінанта коливальна ланка матиме коливання. Причому ці коливання

б

а — зміна вхідної величини; б — зміна вихідної величини.

Рисунок 1.16 – Графік перехідного процесу коливальної ланки

при D > 0.

удуть затухаючими, якщо дійсна частина комплексного кореня буде від’ємною , і зростаючими, якщо дійсна частина комплексного кореня буде позитивною.

Рівняння амплітудно-фазової характеристики

а — відцентровий маятник; б — електричний коливальний контур RLC; в — диференціальний манометр поплавця.

Рисунок 1.18 – Приклади конструктивного виконання коливальної ланки.

коливальної ланки (рисунок 1.17) одержимо шляхом підстановки в передавальну функцію ланки (1.53) значення . Після звільнення від уявної частини в знаменнику і невеликих перетворень одержуємо

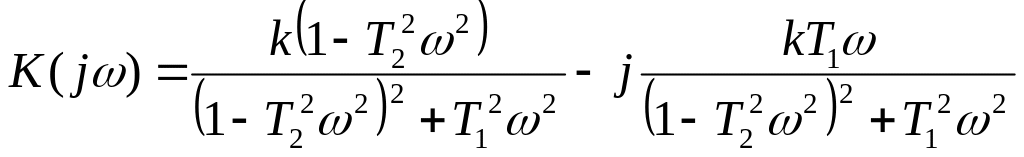. (1.61)

Прикладами конструктивного виконання коливальної ланки можуть служити, наприклад, відцентровий маятник, електричний коливальний контур RLC, поплавковий диференціальний манометр (рисунок 1.18).