9.3. Средние показатели рядов динамики.
Абсолютные и относительные характеристики ряда динамики, рассчитанные по уровням ряда, изменяются во времени. Они варьируют по годам, что требует их обобщения и расчета средних показателей: среднего уровня ряда, средних абсолютных приростов, средних темпов роста и прироста. Часто использование средних показателей ряда динамики становится просто необходимым. Например, сельскохозяйственная продукция в огромной степени зависит от погодных условий данного года, и сравнение годовых показателей становится нецелесообразным. Правильнее сравнивать среднегодовые уровни, среднегодовые абсолютные приросты и темпы роста за определенные промежутки времени.
К среднегодовым показателям приходится прибегать и при невозможности сопоставить абсолютные данные. Например, чтобы определить производство продукции на душу населения, необходимо абсолютный размер производства разделить на численность населения, которая для данного промежутка времени не является постоянной.
Средний уровень интервального ряда динамики определяется как простая средняя арифметическая из уровней за равные промежутки времени:
(9.10)
где п – количество уровней ряда динамики.
Если дан моментный ряд и промежутки времени между датами равны, то средний уровень моментного ряда вычисляется по формуле:
(9.11)
Если дан моментный ряд и промежутки времени между датами не равны, то средний уровень моментного ряда определяется как средняя арифметическая взвешенная.
(9.12)
Средний абсолютный прирост (абсолютное изменение) определяется как средняя арифметическая простая из абсолютных изменений за равные промежутки времени (цепных абсолютных изменений) или как частное от деления базисного абсолютного изменения на число осредняемых отрезков времени от базисного до сравниваемого периода:
(9.13)
где п – число цепных абсолютных приростов.
Средний годовой темп роста определяется как средняя геометрическая цепных темпов роста за п лет (когда известны все показатели) или из общего (базисного) темпа роста за п лет (когда данные пропущены):
(9.14)
Средний темп прироста определяется как разность между средним темпом роста и единицей:
(9.15)
Рассмотренные относительные показатели ряда динамики имеют широкое применение в практической и научной работе. Многие показатели экономического и социального развития государства представлены в виде показателей ряда динамики – общих абсолютных приростов, темпов роста, темпов прироста, средних уровней ряда, средних абсолютных приростов, средних темпов роста и прироста.
Применение перечисленных показателей динамики является первым этапом анализа динамических рядов, позволяющим выявить скорость и интенсивность развития явлений, которые представлены в виде динамического ряда. Дальнейший анализ рядов динамики социально-экономических показателей связан с более сложными обобщениями, с определением основной тенденции, колеблемости уровней и связи рядов.
9.4. Анализ тенденций развития методом укрупнения интервалов.
Одной из задач, возникающих при анализе рядов динамики, является выявление закономерности изменения уровней изучаемого показателя во времени, т.е. выявление основной (общей) тенденции ряда динамики или, иначе говоря, тренда.
Уровни ряда динамики формируются под совокупным влиянием множества длительно и кратковременно действующих факторов и в том числе различного ряда случайных обстоятельств. Тренд – основная закономерность изменения уровней ряда – показывает плавное изменение явления во времени, свободное от всевозможных колебаний и отклонений, вызванных разными причинами. Выявление тренда называется в статистике также выравниванием ряда динамики, а методы выявления основной тенденции – методами выравнивания или сглаживания. На практике выравнивание ряда динамики осуществляется чаще всего следующими методами: укрупнением интервалов, скользящей средней и аналитическим выравниванием. Рассмотрим эти методы.
Если рассматривать уровни экономических и социальных показателей за короткие промежутки времени, то в силу влияния различных факторов, действующих в различных направлениях, в рядах динамики наблюдается их снижение и/или повышение. Из-за этого трудно заметить основную тенденцию развития явления. Одним из наиболее простых приемов обнаружения общей тенденции развития явления является метод укрупнения интервалов ряда динамики. Смысл приема заключается в том, что первоначальный ряд динамики преобразуется и заменяется другим, показатели которого относятся к большим по продолжительности периодам времени, например, ряд, содержащий данные о месячном выпуске продукции, может быть преобразован в ряд квартальных данных. Вновь образованный ряд может содержать либо абсолютные величины за укрупненные по продолжительности промежутки времени (эти величины получают путем простого суммирования уровней первоначального ряда абсолютных величин), либо средние величины. При суммировании уровней или выделении средних по укрупненным интервалам отклонения в уровнях, обусловленные случайными причинами, взаимопогашаются, сглаживаются и более четко обнаруживаются действие основных факторов изменения уровней (общая тенденция)
Пример. В табл. 9.5 приведены сведения о выпуске продукции машиностроительным предприятием за последние десять лет.
Таблица 9.5
Выпуск продукции за последние 10 лет (млн. грн.)
Годы |
1991 |
1992 |
1993 |
1994 |
1995 |
1996 |
1997 |
1998 |
1999 |
2000 |
Объем продукции |
1,25 |
1,03 |
1,35 |
1,20 |
1,25 |
1,31 |
1,40 |
1,07 |
1,52 |
1,21 |
Из-за значительной колеблемости показателя, трудно заметить основную тенденцию выпуска продукции, а значит, сделать вывод о характере работы предприятия.
Выявим тренд с помощью метода укрупнения интервалов, представленный в табл. 9.5 ряд имеет 10 уровней (10 лет). Весь этот временной период разделяем на два равных полупериода (по 5 лет) и для каждого полупериода вычисляем среднюю арифметическую выпуска продукции.
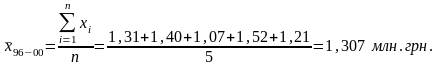
Так как средняя арифметическая за второй период больше средней арифметической первого периода, то можно сделать вывод, что наблюдается устойчивая тенденция к увеличению объема выпуска продукции.