Тема 7. Выборочное наблюдение и проверка гипотез

Цель занятия: сформировать системное представление о выборочном методе.

В результате проведения занятия студент должен:

Знать: сущность таких понятий как выборочный метод, генеральная совокупность, выборка, репрезентативность, основа выборки, бесповторная и повторная выборка, вероятностная и невероятностная выборка, стандартная ошибка статистики, стандартная ошибка среднего, доверительный интервал, уровень доверительности, доверительный интервал предвидения.

Понимать: что выборочный метод является одним из основных методов исследования социально-экономических явлений и потребность в его использовании для выработки вероятностных суждений в современной отечественной практике непрерывно расширяется.

План

7.1. Основные понятия.

7.2. Виды выборок.

7.3. Понятие об ошибке выборки.

7.4. Задачи, решаемые при применении выборочного метода.

7.5. Примеры применения выборочного метода.

7.1. Основные понятия.

Выборочный метод – это система научных принципов случайного отбора определенной части совокупности, которая представляла бы всю совокупность и характеристики которой служили бы надежной основой статистического вывода.

Генеральная совокупность (N) – это изучаемая совокупность (люди, объекты и т.п.) из которой отбираются элементы для обследования.

Выборка (n) – это меньший набор элементов, извлеченных из генеральной совокупности, который подвергается непосредственному обследованию. У отдельных единиц генеральной совокупности должна быть равная возможность попасть в число единиц, подлежащих обследованию, и поэтому отбор производится случайным образом. Выборку используют для изучения системы, которая является настолько большой, что ее полное исследование стоит слишком дорого. Выборка называется малой, если численность ее единиц не превышает 30 ( ).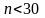

Статистическое наблюдение – это первая стадия всякого статистического исследования, представляющая собой научно организованный по единой программе учет фактов, характеризующих явления и процессы общественной жизни, и сбор полученных на основе этого учета массовых данных.

Единицей наблюдения называется составная часть объекта наблюдения, которая служит основой счета и обладает признаками, подлежащими регистрации при наблюдении.

При выборочном наблюдении имеют дело с двумя категориями обобщающих показателей: долей и средней величиной.

Доля дает характеристику совокупности по альтернативно варьирующему признаку и исчисляется как отношение числа единиц совокупности, обладающих интересующим нас признаком, к общему числу единиц совокупности. Доля в генеральной совокупности обозначается латинской буквой 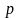, а выборочная доля – .

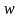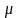Среднее значение варьирующего признака во всей совокупности называется генеральной средней , а среднее значение признака у единиц, которые подверглись выборочному наблюдению, – выборочной средней .

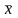Выборку называют репрезентативной, если каждое свойство (или комбинация свойств) наблюдается в выборке с той же частотой, что и в генеральной совокупности.

Многие неверно считают, что большой объем выборки гарантирует ее репрезентативность. Они задают вопрос: как обследование незначительного числа респондентов может дать точные сведения о большом числе людей, которые не были опрошены? Чем больше людей будет опрошено, тем более точные результаты будут получены, считают они.

Однако репрезентативность не зависит от объема выборки. Репрезентативность достигается только тогда, когда в выборку отобраны объекты из разных групп, при условии, что их доли в генеральной и выборочной совокупности равны. Репрезентативность выборки зависит только от методики отбора единиц из генеральной совокупности в выборочную совокупность и не зависит от объема последней. Конечно, чем больше объем выборки, тем выше ее точность, однако, неверно распределенная выборка в 5000 единиц намного хуже, чем хорошо распределенная выборка в 500 единиц.

Чем более однородна генеральная совокупность, тем меньший объем выборочной совокупности потребуется для получения точных результатов. Если, например, в генеральной совокупности все респонденты имеют одинаковый доход, то будет достаточно опросить одного респондента, чтобы узнать средний доход по совокупности. Чтобы определить вкус каши достаточно съесть одну ложку, а не всю тарелку, конечно, при условии, что каша хорошо перемешана.

О выборке, которая не является репрезентативной, говорят, что она имеет смещение. Поскольку выборочная совокупность неточно воспроизводит структуру генеральной, то выборочные оценки также не совпадают с характеристиками генеральной совокупности. Поэтому распространение результатов выборки на всю совокупность связано с ошибкой репрезентативности. Репрезентативность выборки определяется двумя компонентами: ошибками регистрации и случайными ошибками.

Случайные ошибки внутренне присущи выборочному методу – это следствие случайности отбора элементов совокупности для обследования. Они появляются в результате того, что обследуются не все единицы совокупности, а только выборка, и, следовательно, результат будет неточен, так как единицы совокупности не тождественны между собой. Значение случайной ошибки можно сравнительно легко вычислить, используя аппарат, разработанный в статистической теории выборочного метода.

Ошибки регистрации возникают в связи с неправильным установлением факта в процессе наблюдения и бывают двух типов.

Систематической ошибкой регистрации называется ошибка, выражающая некоторые существенные связи, возникающие в процессе регистрации между объектом, субъектом и условиями проведения наблюдения. Систематические ошибки появляются, если при формировании выборочной совокупности нарушен принцип случайности отбора (преднамеренный отбор элементов, несовершенная основа выборки и т.п.). Характерным примером систематической ошибки являются данные о женатых мужчинах и замужних женщинах во Всесоюзной переписи 1970 г. По результатам переписи в целом по Союзу оказалось 53,0 млн. женатых мужчин и 54,2 млн. замужних женщин. Систематическая ошибка, зафиксированная в этой переписи, образовалась из-за погрешностей в ответах, возникающих от различной оценки своего семейного положения мужчинами и женщинами.

Случайные ошибки регистрации отражают менее существенные связи между объектом, субъектом и условиями регистрации и складываются из различных статистических погрешностей в процессе наблюдения. Погрешности, имея различную направленность в отдельных единицах наблюдения, проявляют тенденцию к взаимному погашению при обобщении результатов регистрации по всей исследуемой совокупности.

Для организации простых схем отбора необходима информация обо всех элементах генеральной совокупности или хотя бы их перечень.

Основой выборки называют перечень элементов генеральной совокупности, если он удовлетворяет требованиям полноты, точности, адекватности, удобства работы с ним, отсутствия дублирования единиц наблюдения. Основой могут служить алфавитные списки сотрудников учреждения, номера пропусков, по которым можно идентифицировать определенные единицы, телефонные справочники и т.п.

Бесповторная выборка – если никакой элемент генеральной совокупности не может быть отобран в выборку более одного раза, т.е. единицы совокупности, попавшие в выборку, в дальнейшем в выборке уже не участвуют и численность единиц генеральной совокупности в процессе выборки сокращается.

Повторная выборка – если элемент генеральной совокупности может быть отобран в выборку более одного раза, т.е. единицу генеральной совокупности, попавшую в выборку, после регистрации снова возвращают в генеральную совокупность, и она сохраняет равную возможность с другими единицами при отборе вновь попасть в выборку. При этом методе отбора численность единиц генеральной совокупности остается неизменной. Повторная выборка на практике применяется достаточно редко, т.к. ошибка выборки при бесповторном отборе всегда меньше.

Выборку, которая включает всю совокупность (n = N), называют переписью.

Статистикой, или выборочной статистикой, называют любое число, вычисленное из данных выборки. Параметром или параметром генеральной совокупности, называют любое число, рассчитанное для всей генеральной совокупности.

Оценочная функция (оценка) – это выборочная статистика, которая используется, как предполагаемое значение параметра генеральной совокупности (например, среднее значение выборки). А ее фактическое значение, вычисленное из данных выборки, называют оценкой параметра совокупности.

В практике выборочных наблюдений используют два типа выборочных оценок – точечные и интервальные. Точечная оценка – это значение параметра по данным выборки: выборочная средняя или выборочная доля . Интервальная оценка – это интервал значений параметра, рассчитанный по данным выборки для определенной вероятности, т.е. доверительный интервал.

Случайную выборку, или простую случайную выборку, извлекают таким образом, что: (1) все элементы генеральной совокупности имеют одинаковые вероятности быть отобранными и (2) элементы генеральной совокупности отбираются независимо друг от друга.

Таблица случайных чисел – это, последовательность цифр, в которой все цифры от 0 до 9 появляются независимо друг, от друга и с одинаковой вероятностью 1/7. Использование такой таблицы для последовательного отбора различных элементов генеральной совокупности служит одним из способов извлечения случайной бесповторной выборки.

Всякая статистика, вычисленная на данных случайной выборки, характеризуется вероятностным распределением, которое называют выборочным распределением этой статистики.

Процесс обобщения данных выборки, который приводит к вероятностным утверждениям обо всей генеральной совокупности, называют статистическими выводом.