Тензор напряжений
Рассмотрим точку сплошной среды Р, расположенную на произвольной элементарной поверхности S, определяемой нормалью n (рис. 45). Пусть fi - результирующая сила, с которой материал действует через поверхность на среду, расположенную с положительной стороны поверхности. Средняя сила на единицу площади равна fi /S. Ее величина имеет ненулевой предел, когда AS стягивается в точку Р (принцип Коши). Этот предел называется вектором напряжений или вектором сопротивления Т. Но Т зависит от ориентации площадки элемента поверхности, т.е. от направления нормального вектора n. Таким образом, может показаться, что существует бесконечное количество независимых способов описания напряженного состояния в точке Р. Однако, что оно полностью определяется, если задать компоненты векторов напряжений на трех произвольных взаимно перпендикулярных площадках, проходящих через точку Р, т.е. для полного описания напряженного состояния необходимо знать девять компонент — по три для каждого вектора. Каждую компоненту можно описать двумя индексами: i и j.
Первый индекс указывает ориентацию площадки, второй — направление действия силы.
На рисунке 45 изображены три компоненты для трех плоскостей декартовых координат. Девять компонент векторов напряжения образуют декартов тензор второго порядка - тензор напряжений. Более того, некоторые аргументы, основанные на принципах механики, экспериментальные наблюдения, а также молекулярные теории приводят к заключению, что тензор напряжений симметричен (это справедливо, только для систем в которых отсутствует диффузия, химические реакции и др.):
τij=τji (62)
Рисунок 45 - Компоненты тензора напряжений
12.1 Тензор скоростей деформации
В общем случае течения, возможно девять ненулевых направлений градиента скорости. Каждая из трех компонент скорости может изменяться в трех координатных направлениях, что и дает девять возможных компонент градиента. Таким образом, можно ввести тензор градиентов скорости v, который в декартовых координатах записывается в виде:
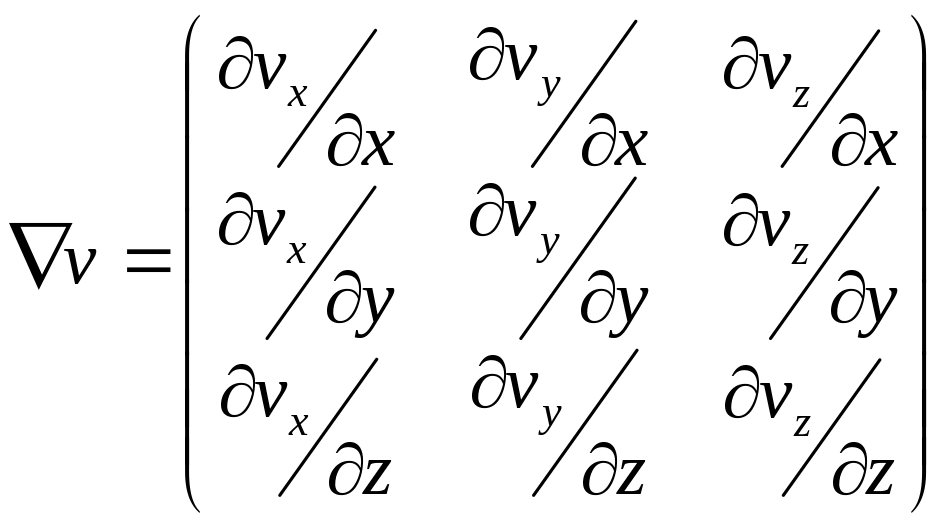(63)
Общие граничные условия и упрощающие предположения
Смазочная аппроксимация
В процессах переработки полимеров часто встречаются ползущие течения в постепенно сходящихся относительно узких каналах. Эти течения обычно аппроксимируются хорошо известным «смазочным» приближением, рассмотренным Осборном Рейнольдсом в его оригинальной работе, в которой он заложил теоретические основы гидродинамики смазки.
Теория рассматривает гидродинамическое поведение тонких пленок жидкости толщиной от долей микрометра до десятков микрометров. В пленках, в результате относительного движения ограничивающих жидкость поверхностей, могут возникать значительные давления (порядка миллионов ньютонов на квадратный метр). При переработке полимеров толщина «пленок», как правило, на несколько порядков больше, но применение для расчета этих процессов допущений, лежащих в основе теории смазки, достаточно обосновано, поскольку вязкость полимерных расплавов на несколько порядков выше вязкости смазочных масел. Вот почему следует кратко рассмотреть основы гидродинамики смазки.
Допущения, на которых основана теория, заключаются в следующем:
а) течение ламинарное;
б)
течение, установившееся во времени (
);
в) течение изотермическое;
г) жидкость несжимаема;
д) жидкость ньютоновская;
е) на стенке нет проскальзывания;
ж) инерционные силы в жидкости пренебрежимо малы по сравнению с силами вязкого сопротивления;
з) любое перемещение жидкости в направлении, нормальном к поверхностям, пренебрежимо мало по сравнению с перемещением в направлении, параллельном ограничивающим поверхностям;
и) течение в поперечном направлении отсутствует.
Приведенная выше система допущений и уравнений (неразрывности и движения) представляет собой смазочную аппроксимацию. Физически это равнозначно утверждению, что, описав локально полностью развившийся поток между параллельными плоскостями с зазором, равным локальному зазору, можно описать фактическое течение.
Однако, применение смазочной аппроксимации при анализе течения вязкоупругих жидкостей не дает достаточной точности.
Тем не менее, подходы и допущения, применяемые в этой теории сильно упрощают решение некоторых практических задач моделирования.
Кроме упомянутых допущений целесообразно ввести еще несколько пунктов:
к) теплоемкость расплава постоянна (не зависит от температуры и давления);
л) теплопроводность расплава постоянна (не зависит от температуры и давления).
В процессах переработки полимеров, где имеют место как теплопередача, так и течение, типичное изменение температуры составляет около 200 °С, а давление изменяется на 50 МПа. При этих условиях плотность типичного полимера будет изменяться на 10 — 20 % в зависимости от того, кристаллический он или аморфный, в то время как вариации k и Ср более значительны и составляют 30 — 40 %.