Розв’язання. 1) Запишемо матрицю

де , і — відповідно сонячна, вітряна та дощова погода.

2) Щоб визначити та , потрібна фундаментальна матриця Z, яка подається через граничну матрицю

Тепер маємо:

звідки

Для визначення знаходимо:

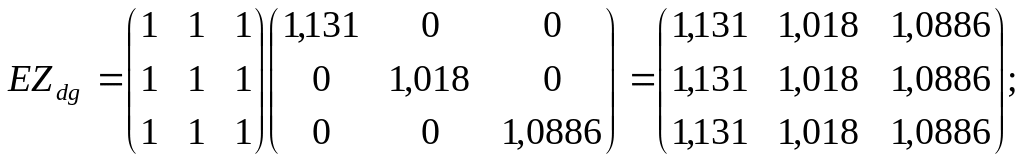
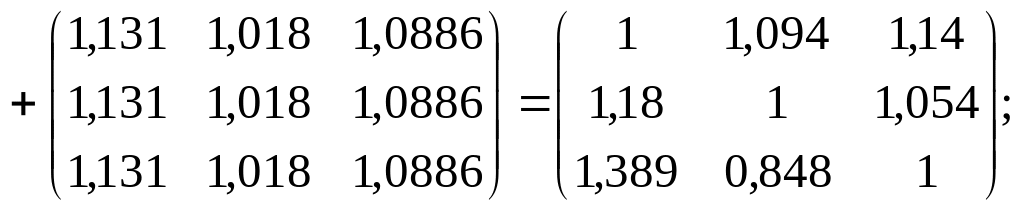
Остаточно маємо:

Отже, якщо сьогодні, наприклад, погода тиха й сонячна, то середня кількість днів до найближчого вітряного дня становитиме 3,6, а до похмурої дощової погоди — 6 (5,905).

Коли ж дощова погода, то середня кількість днів до тихої сонячної погоди наближено дорівнює 3 (2,795).

Щоб визначити , знайдемо:

;

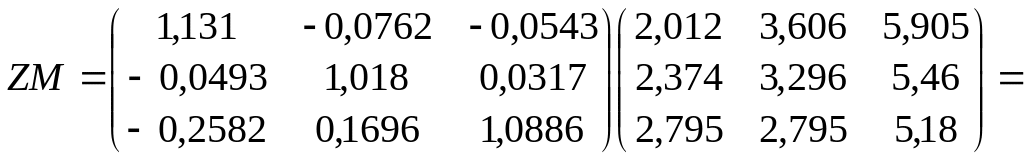
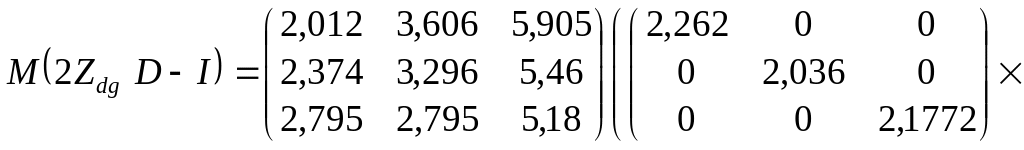
Отже, остаточно дістаємо:

З апитання за темою

1. Означення марковського випадкового процесу.

2. Означення марковського випадкового процесу з дискретними станами та дискретним часом.

3. Що називається ергодичним станом марковського процесу?

4. Який стан марковського процесу називають нестійким?

5. Що називається поглинальним станом?

6. Що називають ланцюгом Маркова?

7. Імовірнісна матриця переходів та її властивості.

8. Що називають умовними ймовірностями переходу системи з одного стану до іншого?

9. Що називають однорідними ланцюгами Маркова?

10. Що називають однокроковою матрицею переходу системи?

11. Як визначаються ймовірності n-крокових переходів системи з одного стану до іншого?

12. Що називають вектором початкового стану системи? Властивості компонентів цього вектора.

13. Що називають поглинальним ланцюгом Маркова?

14. Що називають ергодичним ланцюгом Маркова?

15. Що називають циклічним ланцюгом Маркова?

16. Що називають регулярним ланцюгом Маркова?

17. Імовірнісні моделі та їх властивості.

18. Канонічна форма матриці  для поглинального ланцюга Маркова.

19. Матриця Q та властивості її елементів. Властивості матриці Q.

20. Матриця R та властивості її елементів.

21. Фундаментальна матриця та її властивості.

22. Середнє значення загальної кількості разів перебування системи в одному зі станів

23. Дисперсія перебування системи в одному зі станів

24. Середня кількість кроків, що їх здійснить система, перш ніж набуде поглинального стану; її дисперсія.

25. Визначення ймовірностей, за яких система набуває поглинального стану.

26. Регулярні ланцюги Маркова. Означення стаціонарних імовірностей для цих ланцюгів.

27. Стаціонарний вектор та його властивості.

28. Матриця стаціонарних імовірностей.

29. Фундаментальна матриця для регулярних ланцюгів Маркова.

30. Визначення матриці M.

31. Bластивості елементів матриці M.

32. Визначення матриці

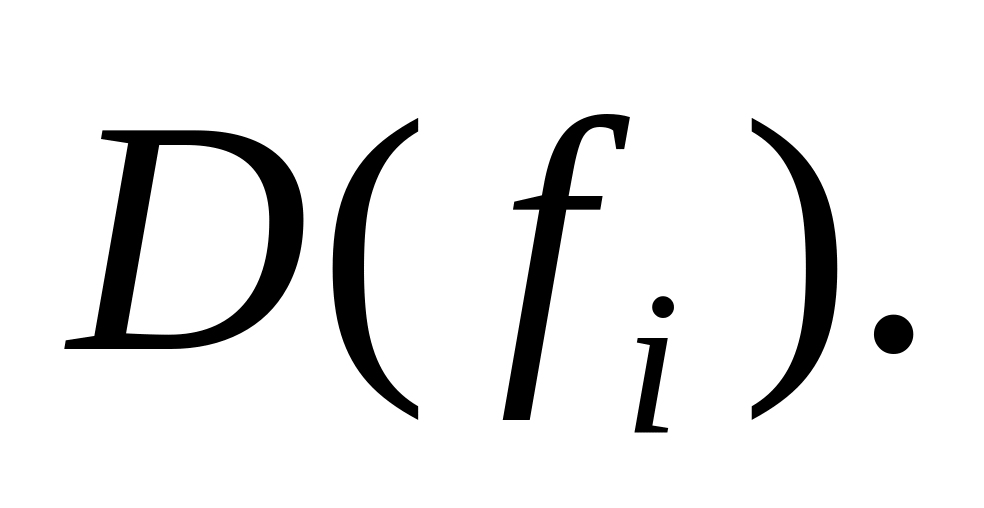
33. Властивості елементів матриці

З адачі за темою

1. На колі розміщено 6 рівновіддалених точок. Із заданої точки (вибраної навмання) процес починає рухатися за таким алгоритмом: імовірність потрапляння в одну з найближчих точок становить 0,4, а в діаметрально протилежну точку — 0,2.

Записати однокрокову матрицю ймовірностей переходу системи та визначити клас ланцюга Маркова, що його моделює матриця. Визначити основні числові характеристики для цього випадкового процесу.

2. За даною матрицею однокрокового переходу

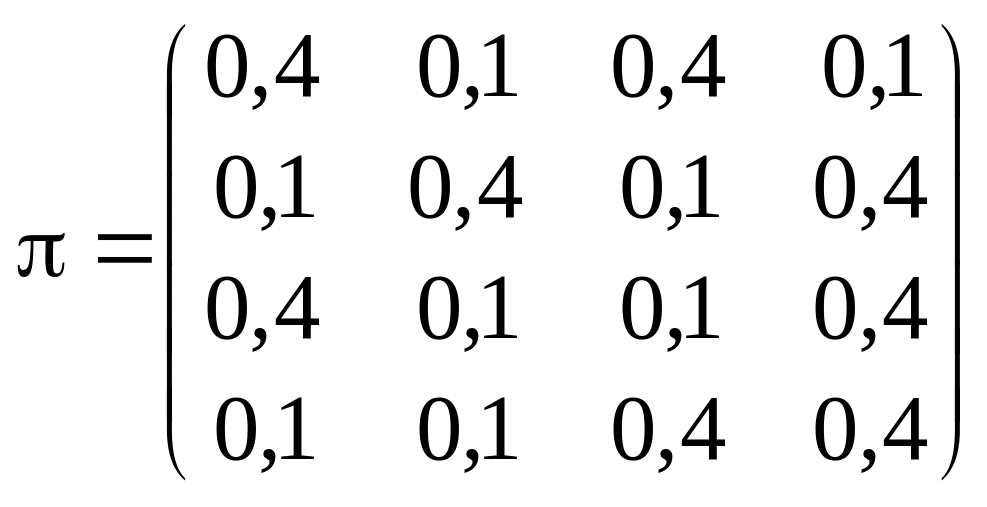
знайти M, D.

3. Матриця  описує поглинальний ланцюг Маркова з чотирма станами серед яких стан є поглинальним. Знайти якщо

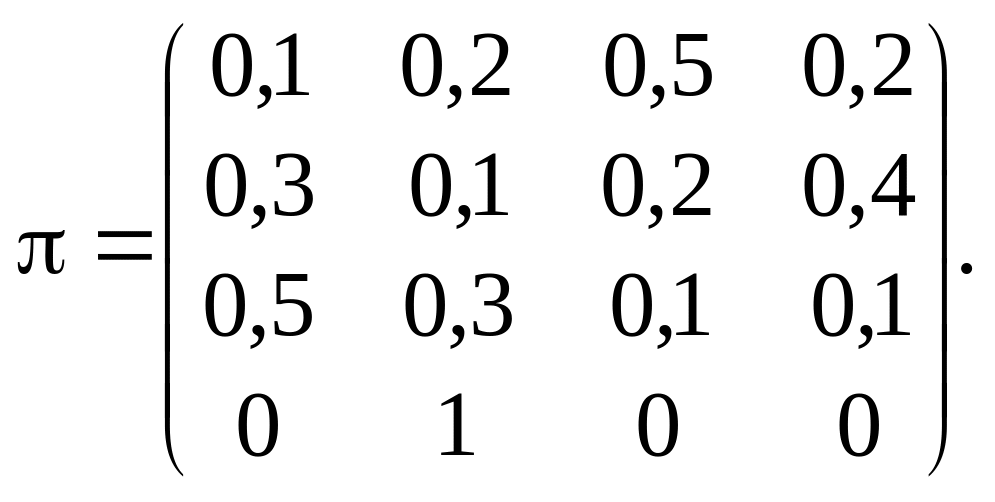
4. За даною однокроковою матрицею

,

яка описує регулярний ланцюг Маркова, знайти стаціонарні ймовірності.

5. За даною матрицею

що описує регулярний ланцюг Маркова, обчислити M і D.