1. Канонічна форма матриці π

Розглядаючи поглинальні ланцюги Маркова, стани процесу нумерують так, щоб поглинальні дістали перші номери.

З огляду на це матриця — вона в такому разі називається канонічною формою матриці π — у загальному випадку подається у вигляді:

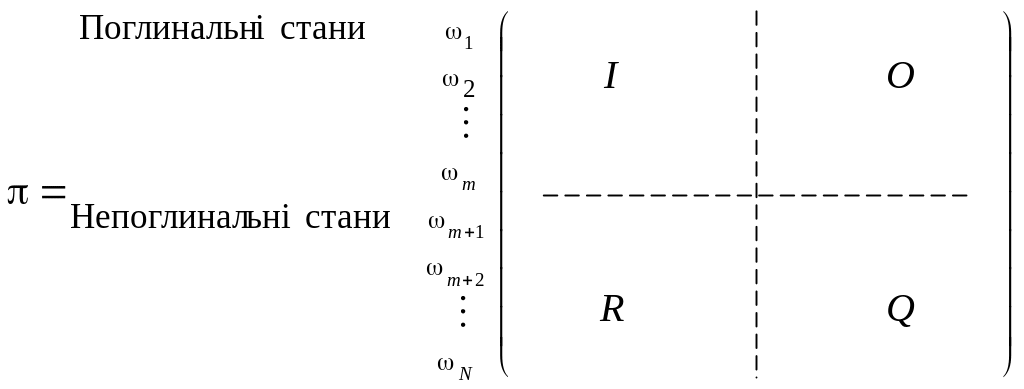. (24)

Тут I — одинична матриця розміром m×m;

O — матриця розміром усі елементи якої дорівнюють нулю;

Q — матриця розміром елементами якої є ймовірності переходів системи з непоглинальних станів до непоглинальних;

R — матриця розміром елементами якої є ймовірності, що визначають перехід системи з непоглинального стану до поглинального.

Приклад 11. За даною матрицею ймовірностей однокрокового переходу поглинального ланцюга Маркова

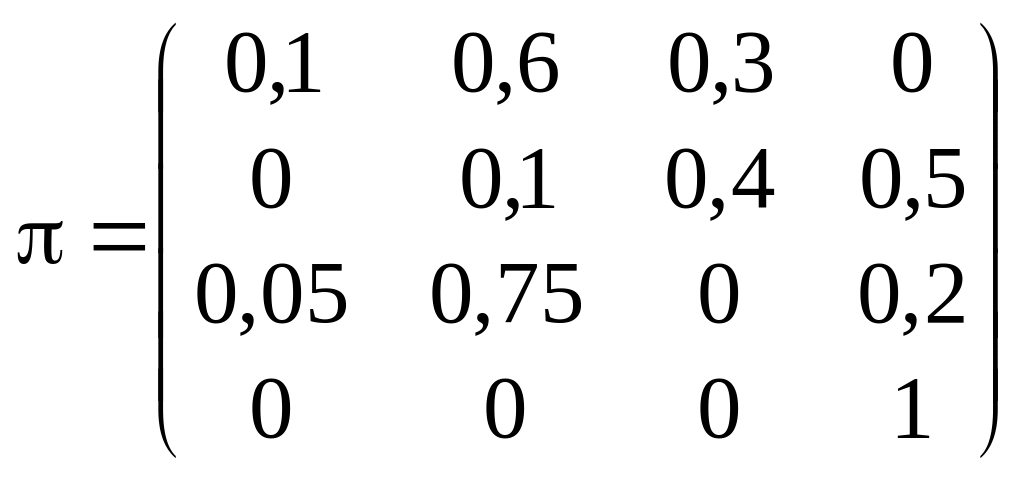
побудувати її канонічну форму.

Розв’язання. Матриця π описує поглинальний ланцюг Маркова з чотирма станами із яких стан є поглинальним.

Тому для матриці

канонічна форма набирає такого вигляду:

,

де

.

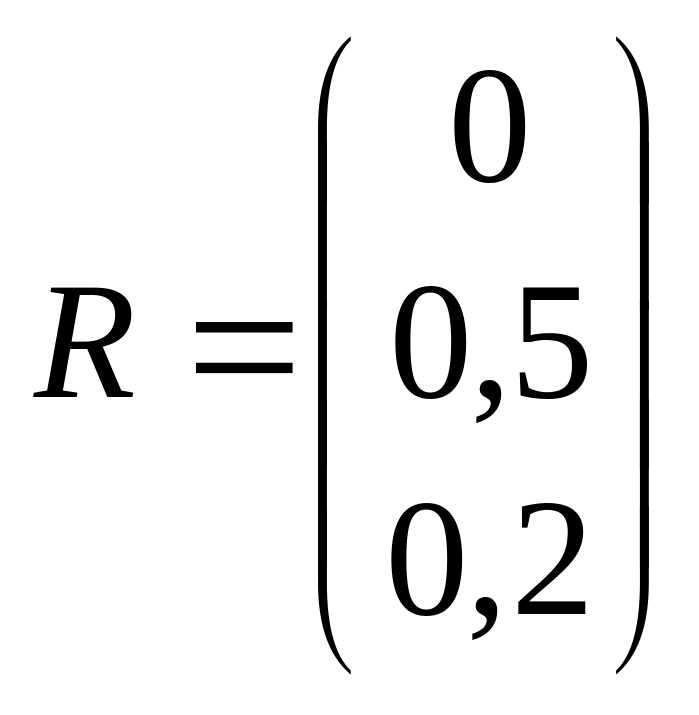Приклад 12. За даною матрицею ймовірностей однокрокового переходу системи

побудувати канонічну матрицю.

Розв’язання. Канонічна форма матриці буде така:

,

де .

2. Фундаментальна матриця

Для поглинального ланцюга Маркова з однокроковою матрицею ймовірностей, поданою в канонічній формі (24), справджуються такі твердження:

1) де О — нульова матриця, всі елементи якої нулі;

2) матриця де І — одинична матриця, має обернену;

3) . (25)

Для поглинального ланцюга Маркова ймовірність переходу системи (процесу) в поглинальний стан зі збільшенням числа кроків переходу k прямує до одиниці. А тому і буде виконуватися рівність

. (26)

Приклад 13. За даною однокроковою матрицею ймовірностей

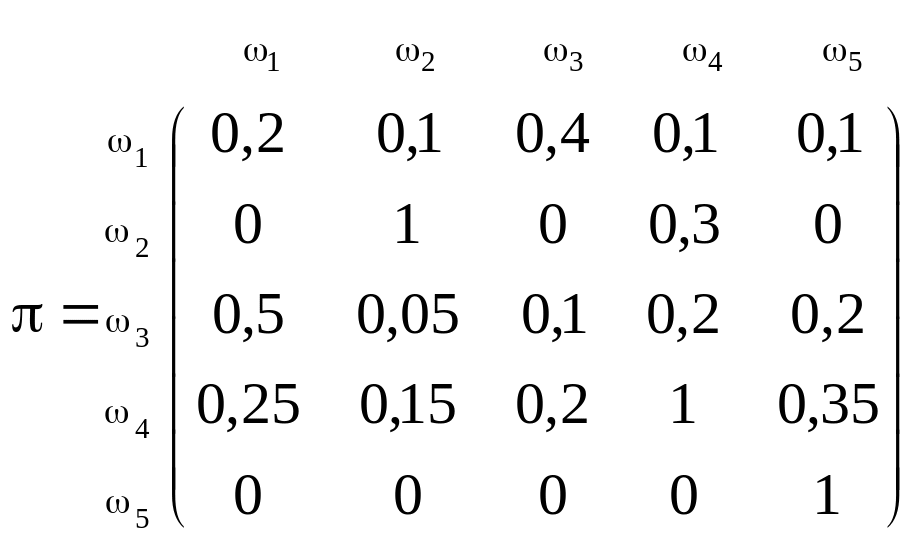
установити, як змінюються значення ймовірностей переходу з одного стану до іншого зі зростанням кількості кроків k.

Розв’язання. Перейдемо від матриці π до її канонічної форми, беручи до уваги, що стани і поглинальні:

.

Отже, маємо:

…

— матриця, елементи якої є ймовірності переходів системи з непоглинальних станів до поглинальних

— матриця, елементами якої є ймовірності переходів системи з непоглинальних станів до непоглинальних (тобто система перебуває лише у станах

Простежимо, як змінюються значення ймовірностей переходу для матриць R і Q зі зміною кількості кроків.

1)  :

.

2)  :

.

Як бачимо, зі зростанням кількості кроків імовірності матриці R збільшуються, а ймовірності матриці Q зменшуються. І вже за матриця набирає такого вигляду:

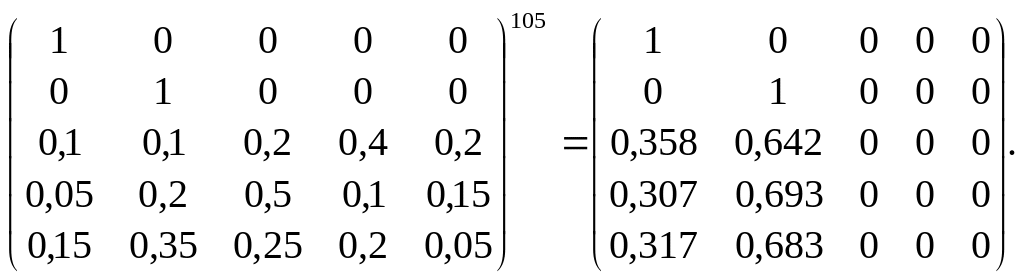
Отже, коли кількість кроків , усі елементи матриці Q дорівнюють нулям, і система може перебувати лише у стані із якого вона неодмінно переходить до одного з поглинальних станів — чи

Матриця матиме обернену лише за умови, що визначник її не дорівнює нулю, тобто

Доведемо, що

Скориставшись властивістю визначника

(27)

розглянемо рівність

звідки

(28) (28)

Отже, а тому для великих значень n (кількості кроків)

Із (27) і (28) випливає, що

Оскільки то матриця має обернену. Із (28) маємо: . Звідси при дістаємо

На практиці обернену матрицю знаходять, здебільшого, традиційними методами.

Матрицю називають фундаментальною для поглинального ланцюга Маркова.

Елемент, який у матриці N міститься на перетині і-го рядка і j-го стовпця, характеризує середнє значення кількості випадків перебування системи (процесу) у стані і позначається .

Фундаментальну матрицю N можна дістати й іншим методом. Справді, нехай — функція, значення якої дорівнює загальній кількості моментів часу, протягом якого система (процес) перебуватиме у стані а — функція, яка може набувати лише двох значень: 1 — з імовірністю коли система на k-му кроці перебуватиме у стані і 0 — з імовірністю у протилежному випадку.

Тоді дістаємо:

(29)

Приклад 14. За даною однокроковою матрицею

,

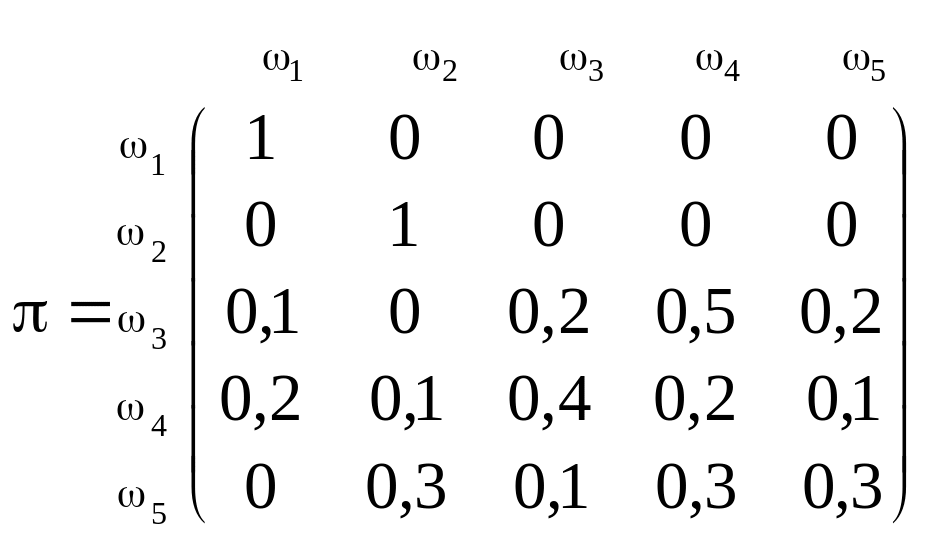яка описує поглинальний марковський процес, знайти фундаментальну матрицю N.

Розв’язання. Визначаємо матрицю Оскільки

то

Звідси

Приклад 15. За результатами обробки статистичної інформації про навчальний процес деякого вищого навчального закладу України дістали такі дані про його середньостатистичного студента:

• студент 1-го курсу з імовірністю 0,1 припиняє навчання через неуспішність, з імовірністю 0,25 ще на рік залишається першокурсником та з імовірністю 0,65 переходить на 2-й курс;

• студент 2-го курсу з імовірністю 0,15 відсівається через неуспішність, з імовірністю 0,3 залишається повторно студіювати 2-й курс, з імовірністю 0,55 переходить на 3-й курс;

• студент 3-го курсу відсівається з імовірністю 0,22, з імовірністю 0,31 стає другорічником, з імовірністю 0,57 переходить на 4-й курс;

• студент 4-го курсу відсівається з імовірністю 0,12, з імовірністю 0,2 стає другорічником, з імовірністю 0,68 переходить на 5-й курс;

• студент 5-го курсу відсівається з імовірністю 0,05, з імовірністю 0,15 стає другорічником, з імовірністю 0,8 захищає дипломну роботу і залишає вуз дипломованим фахівцем.

Побудувати матрицю імовірностей переходу та записати фундаментальну матрицю

Розв’язання. Розглянемо умовно студента як деяку ймовірнісну систему, що може перебувати в одному із семи несумісних станів: — відсіятися через незадовільне навчання; —навчатися на 1-му курсі; — навчатися відповідно на 2-му, 3-му, 4-му та 5-му курсах; — залишити вищий навчальний заклад дипломованим фахівцем. За умовою задачі будуємо матрицю ймовірностей переходу:

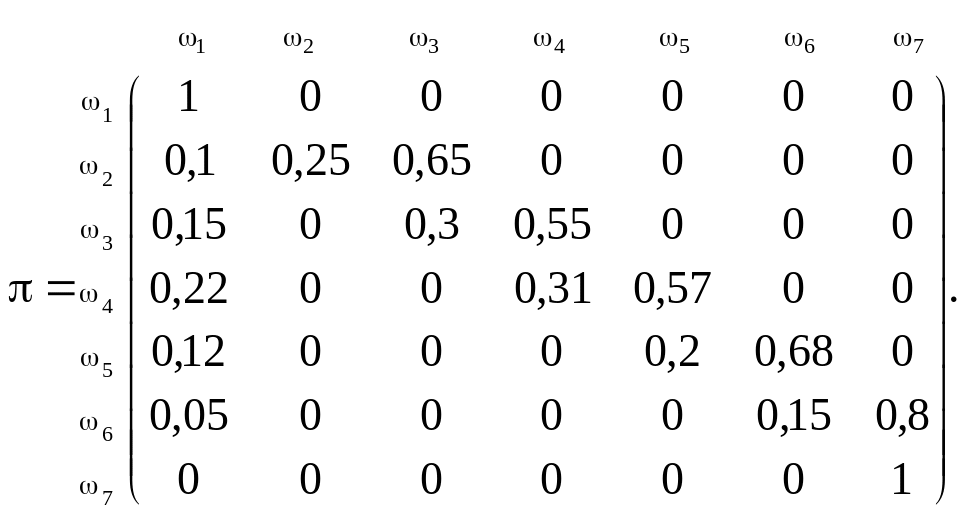
У канонічній формі ця матриця подається так:

Матриця

Матриця

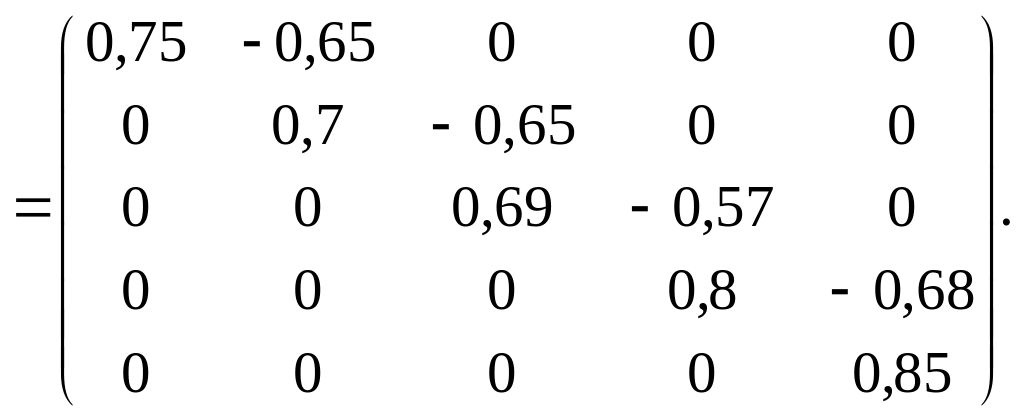
Тоді

Отже, середнє значення (математичне сподівання) часу, протягом якого система (процес) перебуває в одному зі станів , визначається відповідним елементом матриці Так, у розглядуваному прикладі середньостатистичний студент у середньому на 1-му курсі може перебувати 1,33 одиниці часу, на 2-му— 1,24, на 3-му — 1,17, на 4-му — 0,83 і на 5-му курсі — 0,67.

Фундаментальна матриця N застосовується для визначення інших числових характеристик: дисперсії загального часу перебування системи в одному зі станів середньої кількості кроків, що їх зробить система до моменту, коли вона набуде поглинального стану; дисперсії ймовірності того, що система перейде з непоглинального стану до поглинального.