2.7. Класифікація однорідних ланцюгів Маркова
Усі ланцюги Маркова можна поділити на два класи: на ті, які мають нестійкі стани, і на ті, які таких станів не мають.
Ланцюг Маркова називають поглинальним, якщо серед множини станів відповідної системи існує хоча б один, набувши якого з певною ймовірністю, система перебуватиме в ньому й надалі. Отже, поглинальними є такі ланцюги Маркова, для яких стійкими станами є поглинальні.
Приклад 8. Існує гра, яку називають револьверною рулеткою. Правила її такі. Револьвер із шестизарядним барабаном заряджається одним патроном. Гравець натискує курок. У разі першого експерименту можливі два наслідки: — постріл здійсниться; — не здійсниться. Побудувати матриці ймовірностей π та імовірнісний граф.
Розв’язання. Розглянемо цю гру як систему, що має лише два несумісні стани. Тоді матриця ймовірностей переходу складатиметься з двох рядків:
У першому рядку
— імовірність того, що постріл не
відбувся, а тому гра триватиме;
— імовірність того, що постріл відбувся
і гра на цьому закінчилася; другий рядок
Імовірнісний граф зображено на рис. 16.
Рис. 16
Ланцюг Маркова називається ергодичним, якщо він має лише одну ергодичну множину станів системи.
Ергодичні ланцюги Маркова бувають двох типів: циклічні та регулярні.
Ланцюг Маркова називається циклічним, якщо кожного свого стану система може набувати з певною ймовірністю через певні однакові інтервали — періоди.
Приклад 9. За даною матрицею ймовірностей переходу
визначити тип ланцюга Маркова та побудувати імовірнісний граф.
Розв’язання.
Система може
перебувати в трьох несумісних станах
а перейшовши зі стану
до стану
або
,
вона циклічно робитиме перехід
Отже, ланцюг Маркова буде циклічним.
Імовірнісний граф для цього ланцюга зображено на рис. 17.
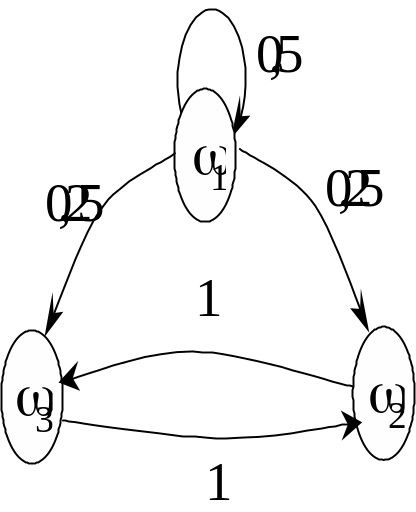
Рис.17
Ланцюг Маркова
називається регулярним,
якщо за певної кількості кроків n
матриця
не матиме нульових елементів, тобто
можливий перехід між будь-якими станами
за n
кроків.
Приклад 10. Споживання електроенергії влітку тісно пов’язане з температурою повітря. Тому, плануючи на кожний день виробництво та використання електроенергії, енергокомпанія, яка забезпечує населення міста електроживленням, має брати до уваги ймовірність спекотної, помірної чи прохолодної погоди. Багаторічні спостереження показали: імовірність того, що завтра буде спекотна, помірна чи прохолодна погода, залежить лише від того, яка погода сьогодні — спекотна, помірна чи прохолодна. Перехідні ймовірності зазначено на ймовірнісному графі (рис. 18), де — спекотна погода, — помірна і — прохолодна.
Побудувати матрицю ймовірностей однокрокового переходу та визначити тип ланцюга Маркова.
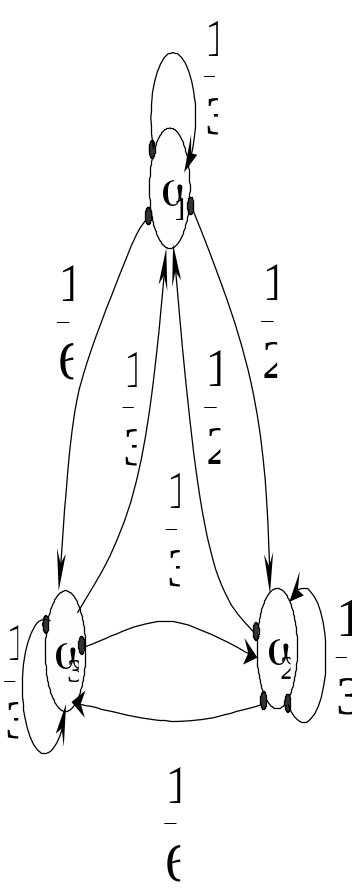
Рис. 18
Розв’язання. Із графа (див. рис. 18) визначаємо ймовірності переходу для рядків матриці π:
Отже, ця матриця матиме такий вигляд:
,
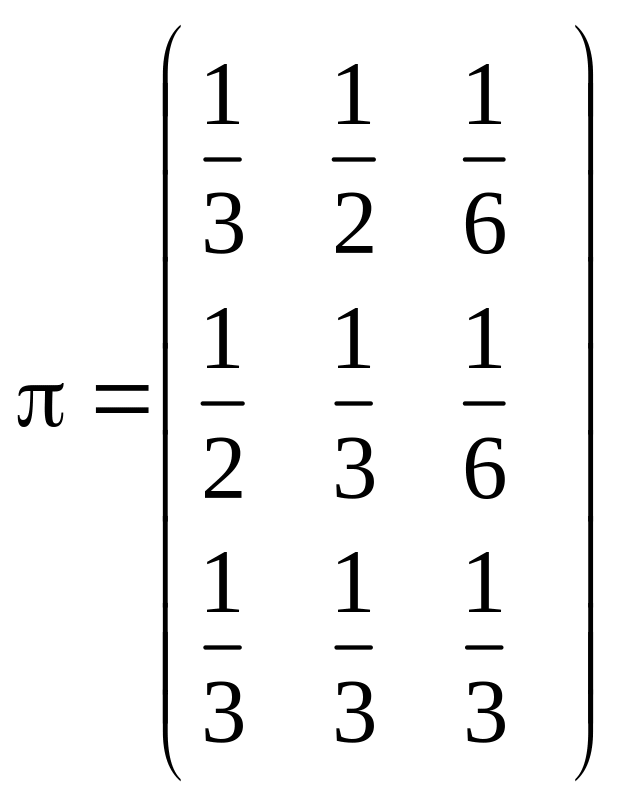тобто дістанемо регулярний ланцюг Маркова.
2.8. Поглинальні ланцюги Маркова та їх основні числові характеристики
Вивчаючи поглинальні ланцюги Маркова, визначають:
1) імовірності переходу до поглинального стану за умови, що процес почався з непоглинального стану;
2) середнє значення часу перебування процесу в непоглинальному стані, перш ніж він перейде до одного з поглинальних станів, за умови, що в початковий момент часу процес був у непоглинальному стані;
3) середню кількість зроблених кроків, перш ніж процес перейде до поглинального стану, якщо початковий стан процесу був непоглинальним.