Тема 2. Марковські випадкові процеси із дискретними станами і часом. Ланцюги Маркова

2.1. Значення марковського випадкового процесу

Серед випадкових процесів марковські становлять окремий клас. Вони посідають важливе місце серед інших з огляду на те, що для них добре розроблено математичний апарат, який дає змогу розв’язувати широке коло прикладних задач. За допомогою марковських процесів можна достатньо точно описати функціонування й розвиток реальних фізичних, економічних, екологічних, соціологічних систем.

Випадковий процес , , називають марковським, якщо для моментів часу умовна функція розподілу для моменту часу випадкового процесу

залежить лише від функції розподілу для моменту часу цього процесу і не залежить від функцій розподілу для

Отже, для марковського випадкового процесу справджується така рівність імовірностей:

. (13)

Таким чином, для марковського випадкового процесу його майбутнє в момент часу залежить від теперішнього моменту часу в якому процес перебуває, а через нього також і від того, в якому стані цей процес перебував у момент часу в минулому. Цю закономірність унаочнює рис. 10.

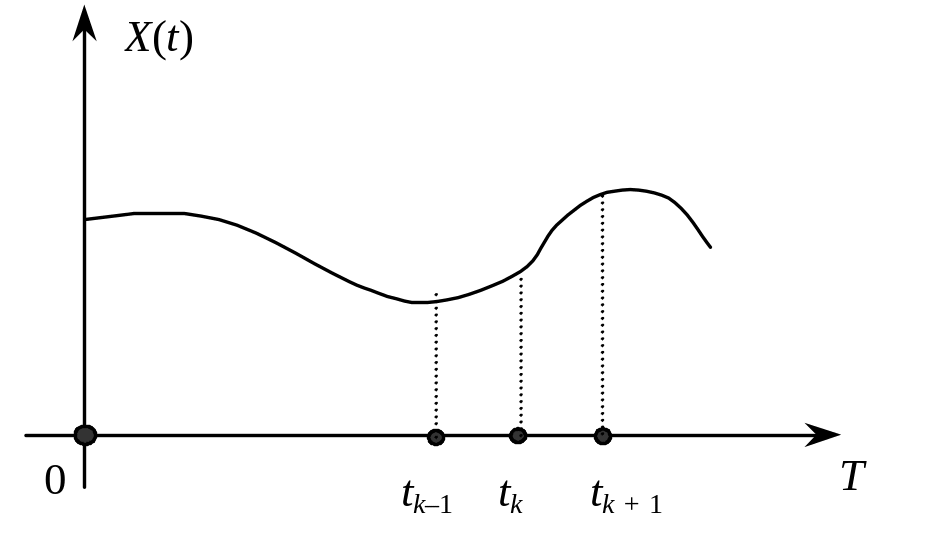
Рис. 10

Наприклад, розвиток енергогенеруючих систем у 2003 році (майбутнє) залежить від діяльності в 2002 році (теперішнє), який, у свою чергу, залежить від їх стану в 2001 році (минуле).

Отже, для марковського випадкового процесу його майбутнє залежить від його минулого лише через теперішнє.

2.2. Марковські випадкові процеси з дискретними станами і дискретним часом. Ланцюги Маркова

Вивчаючи марковські процеси, часто з метою наочного висвітлення цього питання розглядають певну економічну або будь-яку іншу систему А, котра в кожний фіксований момент часу може перебувати в одному з несумісних станів , причому перехід цієї системи з одного стану до іншого може відбуватися в моменти часу  .

Нехай випадковий перехід системи А із одного стану в будь-який можливий інший здійснюється лише в певні моменти часу які називають кроками процесу. Такі процеси називаються марковськими з дискретними станами і дискретним часом. Множину всіх можливих станів системи, в яких може перебувати марковський процес, називають простором станів процесу і позначають Символами позначають конкретні стани процесу.

Запис означає перехід процесу із і-го стану до j-го. Простір станів може бути обмеженим і необмеженим. Далі розглядатимемо марковські процеси з обмеженою кількістю станів простору

Приклад 1. Футбольна команда готується до чергового матчу, результатом якого можуть бути з певною ймовірністю лише три несумісні стани (події): команда виграє — стан нічийний результат матчу — стан команда програє матч — стан Отже,

Перелічені стани є несумісними, і перехід команди в кожний із цих станів може здійснюватися з певною ймовірністю. Розглядаючи команду як систему, можна стверджувати, що в ній відбувається марковський процес із дискретними станами та дискретним часом переходу з одного стану до іншого за один крок (за один матч).

Приклад 2. Фермер купив трактор. У процесі роботи його в господарстві трактор може з певною ймовірністю перебувати в одному з несумісних станів: — роботоздатному; — нероботоздатному. Перехід із одного стану до іншого може відбуватися в дискретні моменти часу.

Отже, випадковий процес, який маємо в системі (тракторі), буде марковським процесом із дискретними станами та дискретним часом. Простір станів