1. Понятие модели. Виды математических моделей.

Для применения методов опт-ии требуется построить мат.модель. Модель - это физический или абстрактный образ моделируемого объекта, удобный для проведения исследований и позволяющий адекватно отображать интересующие исследователя физические свойства и характеристики объекта. Математическая модель – это совокупность математических объектов (числа, переменные, множества, векторы, матрицы) и отношений между ними, адекватно отображающая физические свойства исследуемого объекта.

Математическая модель состоит из:

1. Совокупности неизвестных величин, воздействием на которые систему можно соверш-ть(план задачи, или вектор управления);

2. ЦФ, кот. позволяет выбрать наилучший вариант из возможных;

3. Системы ограничений на неизвестные величины.

Классификация задач оптимизации:

1) Детерминированные; стохастические; задачи оптимизации с неопределённостью. Детерминированная модель отражает поведение системы с позиций полной определённости в настоящем и будущем. Стохастическая(вероятностная) – учитывает влияние случайных факторов на поведение системы и следовательно оценивает будущее с позиций вероятности тех или иных событий. Задача оптимизации с неопределённостью – даёт возможность изучать конфликтные ситуации, в кот. каждая из конфликтующих сторон придерживаетсяся своих взглядов, старается получить информацию о намерениях противника и действует в соответствии со складывающейся обстановкой (игровая модель).

2) Статические и динамические.Статическая модель отражает состояние, в кот. исследуемая система находится в какой-то момент времени. Динамическая – отражает изменения во времени, происходящие в экономической системе, т.е. описывает развитие системы во времени.

3) Задачи безусловной и условной оптимизации.

4) Задачи с непрерывными и дискретными переменными.

5) Однокритериальные и многокритериальные задачи оптимизации.

6) Линейные и нелинейные задачи оптимизации. Если ЦФ и система ограничений представлены линейными функциями нескольких переменных, то это задача лин.программирования. Если ЦФ или одна из функций системы ограничений нелинейны, то это задача нелинейного прогр-ия.

7) Одноэкстремальные и многоэкстремальные задачи оптимизации.

2 .Общая постановка задачи линейного программирования. Графический способ решения задачи линейного программирования.

Линейное программирование – это раздел математического программирования, применяемый при разработке методов нахождения экстремума линейных функций нескольких переменных при линейных ограничениях, налагаемых на переменные.

Главная особенность ЗЛП – экстремум целевой функции находится на границе области допустимых решений (D).

х₂

D Z(x)max

х₁

Z(x) Z(x)min

Математическая модель ЗЛП: max(min) Z = z(x); x D.

Формы записи

1.В виде функций:

Краткая форма

Развёрнутая форма: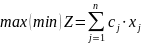

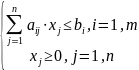
2. Векторная форма

3. Матричная форма

3. Понятие двойственности в задачах линейного программирования (ЗЛП). Правила построения двойственных задач (симметричных и несимметричных).

С каждой ЗЛП тесно связана другая линейная задача, называемая двойственной. Первоначальная задача называется прямой или исходной. Многие ЗЛП первоначально ставятся в виде исходных или двойственных задач, поэтому говорят о паре взаимно двойственных ЗЛП. Пара симметричных двойственных ЗЛП имеет следующий вид:

Прямая задача max Z=

Двойственная задача min Z=

Рассмотренная пара взаимно двойственных задач может быть экономически интерпретирована, например, так.

Прямая задача: сколько и какой продукции хj (j=1,n) надо произвести, чтобы при заданных стоимостях единицы продукции cj (j=1,n), объемах имеющихся ресурсов bi (i=1,m) и нормах расходов aij максимизировать выпуск продукции в стоимостном выражении?

Двойственная задача: какова должна быть оценка единицы каждого из ресурсов yi (i=1,m), чтобы при заданных bi, cj и aij минимизировать общую оценку затрат на все ресурсы.

Правила построения симметричных двойственных задач:

1. Если прямая на max, то двойственная к ней на min и наоборот.

2. Коэф-ты целевой ф-ии прямой задачи явл. свободными членами двойственной.

3. Свободные члены b_i ограничения прямой задачи явл. коэф-ми целевой функции двойственной задачи.

4. Матрицы коэффициентов прямой и двойственной задач явл. транспонированными друг к другу.

5. Если прямая задача на max то ее сист. ограничений представляется в виде неравенств со знаком <=. Двойственная задача решаемая на min и её сист. ограничений имеет вид неравенств со знаком >=.

6. Число ограничений прямой задачи = числу переменных двойственной, а число ограничений двойственной = числу переменных прямой.

7. Все переменные в задачах неотрицательны.

Если среди ограничений прямой задачи имеется равенство или на некоторые переменные не накладывается условие не отрицательности, то построив двойственную линейную задачу, получим пару несимметричных задач.

Правила построения несимметричных двойственных задач:

1. Если на переменную x_j прямой задачи накладывается условие неотрицательности, то j-ое условие системы ограничений двойственной задачи явл. неравенство.

2. Если на x_j прям. задачи не накладывается условие неотрицательности, то j-ое ограничение системы двойственной задачи записывается в виде строгого равенства.

3. Если в прямой задаче имеются ограничения равенства то на соотв. переменные двойственной задачи не накладываются условие неотрицательности.