
Лабораторная работа № 4
ИССЛЕДОВАНИЕ ТИПОВЫХ ДИНАМИЧЕСКИХ ЗВЕНЬЕВ
4.1. Цель работы
Целью работы является изучение свойств и процессов в типовых динамических звеньев САУ. В результате выполнения работы курсант должен знать типовые звенья САУ, их уравнения динамики и передаточные функции, особенности временных и частотных характеристик.
4.2. Теоретическая часть
Для теоретического исследования САУ удобно классифицировать их элементы (звенья) не по конструктивным признакам, а по динамическим свойствам, т.е. по их поведению в переходных процессах. Это поведение зависит от вида алгоритма, который связывает их входные и выходные величины. Динамические звенья рассматриваются как удобный «строительный» материал для разработки систем управления, поскольку процессы, протекающие в отдельных звеньях, проще поддаются описанию, чем во всей системе управления.
Особенно удобно для целей исследования разделение САУ на простейшие звенья, описываемые дифференциальными уравнениями не выше второго порядка. Такие звенья называются типовыми звеньями. Все типовые звенья можно разделить на 3 группы в зависимости от поведения их в установившемся режиме:
позиционные (в установившемся режиме выходная величина прямо пропорциональна входной);
интегрирующие (выходная величина изменяется в одном направлении до тех пор, пока на входе есть отличный от нуля сигнал),
дифференцирующие (в установившемся режиме выходной сигнал равен нулю, поскольку выходная величина определяется производной от входного сигнала).
Временные
характеристики
звеньев описывают реакцию звена на
специальные входные воздействия в виде
единичной ступенчатой функции и
единичного δ-импульса, а частотные
характеристики описывают
поведение звена в режиме вынужденных
установившихся колебаний. Эти функции
в такой же степени описывают систему,
как и передаточная функция звена
 .
Каждую из этих характеристик можно
экспериментально измерить или рассчитать,
зная передаточную функцию звена. Так,
в частности, АЧХ, которая показывает
как изменяется амплитуда установившихся
колебаний, можно вычислить как модуль
комплексно-частотной характеристики
(КЧХ)
.
Каждую из этих характеристик можно
экспериментально измерить или рассчитать,
зная передаточную функцию звена. Так,
в частности, АЧХ, которая показывает
как изменяется амплитуда установившихся
колебаний, можно вычислить как модуль
комплексно-частотной характеристики
(КЧХ)
 .,
а ФЧХ, которая определяет сдвиг фаз
входных и выходных колебаний, рассчитывается
как аргумент этой функции.
.,
а ФЧХ, которая определяет сдвиг фаз
входных и выходных колебаний, рассчитывается
как аргумент этой функции.
Временные
характеристики звеньев позволяют
рассчитать реакцию звена на произвольное
входное воздействие
 с помощью интегралов свертки Дюамеля:
с помощью интегралов свертки Дюамеля:
 (4.1)
(4.1)
или же
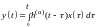 (4.2)
(4.2)
В табл. 4.1 приведена классификация динамических звеньев с указаниями выражений для их передаточных функций, а также временных и частотных характеристик.
Табл. 4.1. Типовые звенья и их передаточные функции
№ п/п |
Класс Звеньев |
Название |
Передаточная функция |
Характеристики |
1 |
Позиционные |
Безынер-ционное |
|
|
2 |
Аперио-дическое 1 порядка |
|
|
|
3 |
Аперио-дическое 2 порядка
|
|
, |
|
4 |
Коле- бательное
|
|
||
5 |
Консер- вативное
|
|
||
6 |
Интегрирующие |
Идеальное интегри- рующее |
|
|
7 |
Интегри-рующее. с замедлением |
|
|
|
8 |
Изодром- ное |
|
|
|
9 |
Дифф. |
Идеальное дифферен-цирующее |
|
высокие и узкие импульсы,
|
10 |
Дифферен- цирующее с замед- лением |
|
|
Здесь использованы следующие обозначения:
 – коэффициент усиления,
– коэффициент усиления,
 –
постоянная времени,
–
постоянная времени,
 – коэффициент демпфирования,
– коэффициент демпфирования,
 –
время интегрирования (дифференцирования)
соответственно, α и β – вещественная и
мнимая части корней характеристического
уравнения.
–
время интегрирования (дифференцирования)
соответственно, α и β – вещественная и
мнимая части корней характеристического
уравнения.
В первой части работы исследуются временные характеристики звеньев. Вначале следует получить переходную и импульсную переходную функции, используя формулы, приведенные в табл. 4.1, и сравнить с результатом вычисления по заданной передаточной функции. Такой расчет по передаточной функции звена удобно выполнять в рамках пакетов компьютерной математики Matlab или Mathcad.
В пакете Matlab расчет временных характеристик следует выполнять c использованием команд приложения CST – step и impulse.
В пакете Mathcad эта задача решается путем формул Солодовникова, которые получены из соотношений обратного преобразования Лапласа:
 (4.3)
(4.3)
 (4.4)
(4.4)
Проиллюстрируем
это на примере звена с передаточной
функцией
 .
Перепишем выражение для передаточной
функции в виде −
.
Перепишем выражение для передаточной
функции в виде −
 .
Следовательно, это апериодическое звено
1 порядка, причем
.
Следовательно, это апериодическое звено
1 порядка, причем
 и
и
 .
Переходная функция его задается
выражением
,
а импульсная переходная – выражением
.
.
Переходная функция его задается
выражением
,
а импульсная переходная – выражением
.
Пакет Matlab
k=0.4; T=0.6; t=0:0.1:5; s=tf('s'); w=2/(3*s+5);
h1=k*(1-exp(-t/T)); h2=step(w,t); h1i=(k/T)*exp(-t/T);h2i=impulse(w,t);
subplot(1,2,1); plot(t,h1,'-',t(1:5:end),h2(1:5:end),'+'); grid on;
subplot(1,2,2); plot(t,h1i,'-',t(1:5:end),h2i(1:5:end),'+'); grid on;

Рис. 1. Переходная и импульсная переходная функции звена вычисленные различными методами.
Пакет Mathcad

Рис.2. Фрагмент документа Mathcad по расчету временных характеристик звена
Заметим, что верхний предел в интегралах вместо бесконечности можно заменить на достаточно большое число.
Далее
следует рассчитать реакцию звена на
входной сигнал произвольного вида с
использованием формул свертки (4.1) –
(4.2), а затем провести проверку расчета
используя приложение Simulink.
Эти действия также удобно выполнять в
рамках одного из пакетов компьютерной
математики. В пакете
Matlab
для вычисления
интеграла свертки (4.2) удобно использовать
М-файл, текст которого приведен ниже
для вышерассмотренного апериодического
звена первого порядка и входного
воздействия в форме −

function f=Fy(t,H)
k=0.4; T=0.6;
hi=@(tau,x)(k*exp(-(x-tau)/T)./T);
X=@(tau)exp(-tau).*sin(3*tau);
y=@(tau,x)hi(tau,x).*X(tau);
y1=@(x)quad(@(tau)y(tau,x),0,x);
N=round(t/H);
t1=zeros(1,N); Y=zeros(1,N);
for m=1:N;
t1(m)=H*m;
Y(m)=y1(H*m);
end
plot(t1,Y,'r+'); hold on; grid on;
f=[t1;Y]';
Результаты расчета выходного сигнала в рамках пакета Simulink и методом вычисления интеграла свертки представлены на рис. 3 и рис.4.
Рис. 3 S-модель определения реакции апериодического звена 1 порядка на произвольный входной сигнал |
Рис.4. Выходная реакция звена апериодического звена второго порядка, вычисленная различными способами |
Аналогичные действия можно выполнить в рамках пакета Mathcad. Несложно также выполнить совмещение этого результата расчета с тем, который выполнялся в пакете Simulink.
Рис.5. Фрагмент документа Mathcad расчета реакции динамического звена на входной сигнал произвольной формы с помощью интеграла свертки |
Во второй части работы исследуются частотные характеристики звена. Необходимо двумя различными способами – по известной аналитической формуле и по заданной передаточной функции рассчитать и построить графики ЛАЧХ и ФЧХ. Проиллюстрируем это на примере изучаемого звена в рамках двух пакетов компьютерной математики.
Скрипт команд в Command Window пакета Matlab имеет вид:
>> om=0.001:0.001:10;
>> k=0.4; T=0.6; L1=20*log10(k)-20*log10((1+om.^2.*T.^2).^0.5); fi1=-atan(om*T);
>> w=tf(2,[3 5]); R=freqresp(w,om); R=R(:); A=abs(R); L2=20*log10(A); fi2=angle(R);
>> subplot(1,2,1); semilogx(om,L1,'-',om(1:250:end),L2(1:250:end),'+'); grid on;
>> subplot(1,2,2); semilogx(om,fi1,'-',om(1:200:end),fi2(1:200:end),'+'); grid on;
Рис.6. Частотные характеристики апериодического звена 1 порядка построенные различными способами |
Аналогичные операции в пакете Mathcad представлены ниже.
Рис.7. Фрагмент документа Mathcad расчета различными способами частотных характеристик динамического звена |


 ,
,
 ,
,
 ,
,
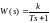
 ,
,
 ,
,
 ,
,


 ,
, ,
,





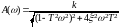









 ,
,


 ,
, ,
, ,
,

 ,
,

 ,
,

 − бесконечно-
− бесконечно-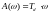 ,
,




 ,
, .
.



