Решение.

Для решения данного неравенства воспользуемся методом интервалов. Вспомним, что дробь может поменять знак лишь в тех точках, в которых или числитель или знаменатель дроби обращается в ноль. Конечно, для данного неравенства не получится применить правило чередования знаков, как это делается с обычной рациональной дробью, поэтому на каждом из интервалов знак будем проверять отдельно.

Итак, нули знаменателя:

.

Для нахождения нулей числителя решим уравнение:

Решить данное уравнение проще всего можно, возведя в квадрат обе части уравнения. Это возведение не приведет к появлению посторонних решений, так как обе части уравнения положительны.

Имеем

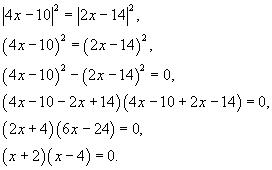
Таким образом, нулями числителя являются .

Полученные четыре значения переменной x разбивают числовую прямую на промежутки. Обозначим их на рисунке.

Точки  и  выкалываются, так как в этих точках знаменатель обращается в ноль. Точки -2 и 4 закрашиваются и включаются в множество решений неравенства, так как неравенство нестрогое.

Теперь на каждом из интервалов выбираем точку и определяем знак выражения    в этой точке.

На основании проведенных расчетов расставляем знаки неравенства:

Записываем решение неравенства: .

Выписываем целые решения неравенства: . Их сумма равна 7.

Ответ: 7

 

Задача В10. Куб вписан в правильную четырехугольную пирамиду так, что четыре его вершины находятся на боковых ребрах пирамиды. А четыре другие вершины – на ее основании. Длина стороны основания пирамиды равна 2, высота пирамиды – 6. Найдите площадь S поверхности куба. В ответ запишите значение 4S.

Решение.

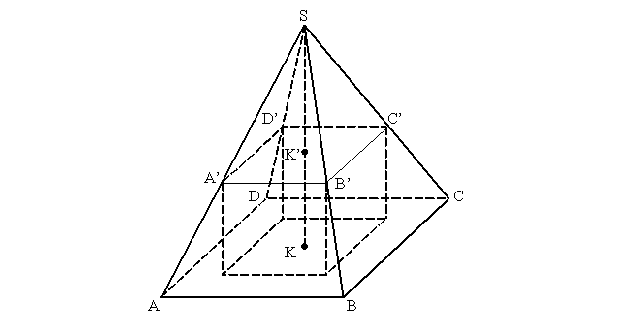
Пусть SABCD - правильная четырехугольная пирамида, в основании которой лежит квадрат ABCD. SK = 6 - высота пирамиды.

Так как 4 вершины нижней грани куба находятся на основании пирамиды, то вся грань лежит в плоскости основания. Верхняя грань куба A'B'C'D', таким образом, параллельна плоскости основания. Поэтому отсекаемая от пирамиды SABCD пирамида SA'B'C'D' подобна исходной.

Запишем соотношение подобия для этих пирамид:

Но , так как  - расстояние между гранями куба, которое равно длине ребра.

Обозначив длину ребра куба через x, получаем:

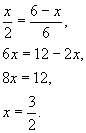
Тогда площадь грани куба: , а площадь поверхности: .

В ответ записываем .

Ответ: 54.

 

Задача В11. Найдите значение выражения .

 

Решение.

Сначала разберемся с тангенсом. Угол  (172 градуса, 30 минут) равен , так как в одном градусе 60 минут.

Тогда

.

Рассчитаем . Это можно сделать различными способами, однако, в каждом из них нам понадобятся формулы двойного угла:

.

Тогда

.

Знак «+» перед скобками выбран потому, что угол  лежит в первой четверти.

Для нахождения  можно воспользоваться формулой косинуса разности:

.

Тогда

.

Числитель и знаменатель подкоренного выражения умножим на  и воспользуемся разностью квадратов в знаменателе:

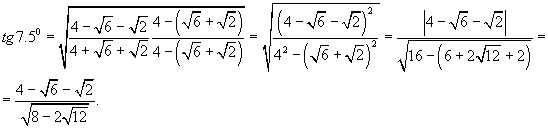
Модуль в числителе раскрыт со знаком «+», так как подмодульное выражение положительно.

Далее выделим полный квадрат под корнем в знаменателе:

При раскрытии модуля в числителе нужно поменять знак, так как подмодульное выражение отрицательно.

Числитель и знаменатель полученного выражения умножаем на , чтобы в знаменателе воспользоваться разностью квадратов и избавиться от иррациональности:

Вычисляем значение исходного выражения:

Ответ: -9.

Задача В12. Трое рабочих (не все одинаковой квалификации) выполняли некоторую работу, работая поочередно. Сначала первый из них проработал  часть времени, необходимого двум другим для выполнения всей работы. Затем второй проработал  часть времени, необходимого двум другим для выполнения всей работы. И, наконец, третий проработал  часть времени, необходимого двум другим для выполнения всей работы. Во сколько раз быстрее работа была бы выполнена, если бы трое рабочих работали одновременно? В ответ запишите найденное число, умноженное на 4.