Подробные решения задачи из варианта 1 части В. ЦТ по математике 2014 г.

25.08.14

Вариант 1

Часть В

Задача В1. Найдите сумму целых решений (решение, если оно единственное) системы неравенств

Решение.

Система из двух квадратных неравенств. По сути, ничего сложно для более или менее подготовленных абитуриентов. Каждое неравенство решается методом интервалов и находится пересечение решений.

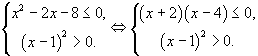
Таким образом, решение системы неравенств имеет вид:

.

Выпишем целые решения, входящие в полученный интервал:

.

Их сумма равна 6.

Ответ: 6.

 

Задача В2. Найдите произведение большего корня на количество корней уравнения .

Решение.

Преобразуем исходное уравнение:

Введем замену переменной .

Тогда уравнение примет следующий вид:

ОДЗ: .

Тогда, умножив обе части уравнения на t, получим

.

Корни этого уравнения на основании обратной теоремы Виета равны:

.

Тогда на основании введенной выше замены получаем совокупность двух уравнений:

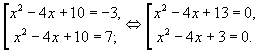
Первое уравнение совокупности не имеет решений, так как его дискриминант отрицателен.

Корни второго уравнения: .

В ответ записываем  (больший корень умножается на количество уравнений)

Ответ: 6.

 

Задача В3. В окружность радиусом 6 вписан треугольник, длины двух сторон которого равны 6 и 10. Найдите длину высоты треугольника, проведенной к его третьей стороне.

Решение.

Выполним вспомогательный чертеж для решения задачи. Пусть АВС – заданный треугольник, у которого .

Проведем высоту  треугольника.

В подобных задачах самый сложный момент – это понять, как связать параметры треугольника (углы или стороны) с параметрами окружности. Ведь задачу мы решаем про треугольник, однако, поскольку дан радиус описанной окружности, то это нужно как-то использовать для получения недостающих сведений о самом треугольнике.

Одна из самых известных связей между треугольником и описанной окружностью доказывается в теореме синусов. Запишем выводы этой теоремы для угла :

Здесь R - радиус описанной около треугольника окружности. Отсюда получаем:

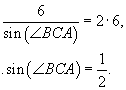
Значит, .

Высоту ВК найдем из прямоугольного треугольника BKA:

.

Ответ: 5

 

Задача В4. Найдите сумму наименьшего и наибольшего целых решений неравенства

.

Решение.

Найдем ОДЗ для x, удовлетворяющих данному неравенству.

Ограничения на x могут наложить логарифмические функции в силу их свойств. В нашем случае получаем:

.

Используя свойства логарифмов, преобразуем исходное неравенство:

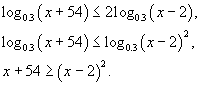
Самым «тонким» моментом в приведенной цепочке преобразований является изменение знака неравенства на противоположный. Это происходит потому, что основания логарифмов меньше единицы.

Осталось решить записанное квадратное неравенство и наложить на него условие из ОДЗ:

Корнями квадратного уравнения  являются числа , поэтому квадратный трехчлен  раскладывается на множители: .

Получаем неравенство , которое решаем методом интервалов:

На рисунке указана, также, область, соответствующая ОДЗ.

Тогда

.

Наименьшим целым числом из данного интервала является 3, а наибольшим – 10. Их сумма равна 13.

Ответ: 13.

 

Задача В5. Найдите сумму (в градусах) наименьшего положительного и наибольшего отрицательного корней уравнения .

Решение.

Преобразуем уравнение, используя формулу двойного аргумента для синуса в левой части:

Далее вспоминаем магическую фразу: «Произведение может равняться нулю только тогда, когда хотя бы один из сомножителей равен нулю».

Получаем совокупность двух уравнений:

Так как , то

Из условия задачи следует, что необходимо найти самые близкие к нулю корни уравнения. Так как n и k могут принимать любые целые значения, то, вообще, корней исходного уравнения существует бесконечное множество. Поэтому проще всего ответить на вопрос задачи можно следующим образом: перебрать все корни, близкие к нулю, и выбрать из них наибольший и наименьший.

Для этого составим таблицу:

n	-1	0		k	0	1	-1	-2

Очевидно, что при остальных n и k ближе к нулю мы уже не подойдем.

Итак, из приведенных значений наименьшим положительным является , а наибольшим отрицательным - .

Сумма полученных углов равна -15.

Ответ: -15.

 

Задача В6. Три числа составляют геометрическую прогрессию, в которой . Если второй член прогрессии уменьшить на 8, то полученные три числа в том же порядке опять составят геометрическую прогрессию. Если третий член новой прогрессии уменьшить на 25, то полученные числа составят арифметическую прогрессию. Найдите сумму исходных чисел.