2. Построение математической модели

Цель: найти план раскроя , обеспечивающий максимальное число комплектов.

Максимизировать нужно число изделий для каждого материала.

где a – изделие; i – способ раскроя; j – материал;

Ограничения будут выглядеть следующим образом:

Запишем условия задачи в виде математических формул.

1. Выберем переменные задачи: x1, x2,…, xn – количество материалов.

2. Составим ограничения задачи: Ограничения по условиям задачи должны обеспечить раскрой материала на изделия в количестве пропорциональном b1, b2,…,bm соответственно.

Так как I – й материал возможно раскроить на ai1 количество изделий, то xi - е единиц I – го материала возможно раскроить на ai1xi количество изделий.

Значит, общее количество изделий из общего числа материалов будет равно сумме:

a11x1 + a21x2+… +an1xn ≥ b1;

Записывая аналогичные условия для изделий, получим:

a11x1 + a21x2+… +an1xn ≥ b1;

a12x1 + a22x2+… +an2xn ≥ b2;

a1mx1 + a2mx2+… +anmxn ≥ bm;

Нельзя забывать очевидно вытекающие из условий задачи ограничения:

X1≥0, X2≥0, …, Xn ≥0

Эти ограничения означают, что отрицательное количество материала Xi не имеет содержательного смысла.

3. Составим целевую функцию. Так как общая длина материала L = C1X1+C2X2+,…,+CnXn, необходимо минимизировать линейную функцию L.

Итак, математическая модель рассмотренной задачи о оптимизации использования материала имеет следующий вид:

Минимизировать L = C1X1+C2X2+,…,+CnXn,

При условиях:

a11x1 + a21x2+… +an1xn ≥ b1;

a12x1 + a22x2+… +an2xn ≥ b2; (3)

a1mx1 + a2mx2+… +anmxn ≥ bm;

X1≥0, X2≥0, …, Xn ≥0.

Или в матричном виде:

cx → min, (4)

Ax ≥ b, x ≥ 0.

3. Численный метод решения задачи лп

3.1. Симплекс – метод

Рассмотрим задачу ЛП в канонической форме:

(5)

……………………… (6)

(7)

Будем предполагать, что (иначе, умножим соответствующее уравнение на -1), уравнения системы (6) линейно независимы, m<n и система (6) -(7) совместна.

При сделанных предположениях можно выбрать m неизвестных (к примеру ) таких, чтобы определитель, составленный из коэффициентов при этих неизвестных, не обращался в ноль. Тогда задача (5) - (7) может быть приведена к виду, который называется специальной формой задачи ЛП:

…………………………………….. (8)

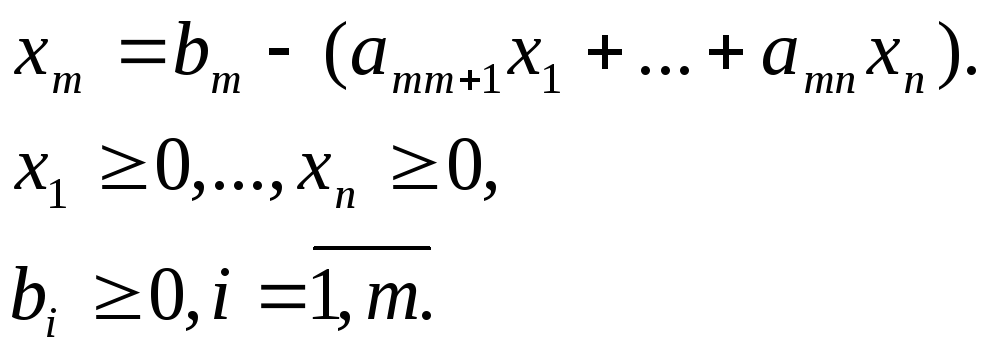
Одно из допустимых решений этой задачи можно найти, если переменные положить равными нулю. Такое решение называется допустимым базисным решением. Оно имеет вид:

Этому решению соответствует значение целевой функции . Переменные называют базисными, набор переменных называют базисом, а переменные называют небазисными или свободными. Число возможных базисов в задаче размерности n с m ограничениями не превосходит величину .

Известно, что каждому допустимому базисному решению соответствует вершина многоугольника допустимых решений и оптимальное решение задачи (при условии его существования) достигается в одной из вершин многоугольника. Поэтому оптимальное решение задачи ЛП находится среди допустимых базисных решений. Существуют рациональные способы последовательного перебора допустимых базисных решений, которые позволяют рассматривать не все допустимые базисные решения, а их минимальное число. К таким методам относится симплекс-метод [1,2,3].