2.4. Пример

Решить графически задачу ЛП, заданную в канонической форме:

(6)

(7)

(8)

Число уравнений задачи m=3, число неизвестныхn=5. Тогдаn-m=2 и задача может быть сведена к задаче на плоскости относительно свободных переменных.

Возьмем в качестве базисных переменныеи выразим их черезсвободные (небазисные переменные):

(9)

По условию (8) переменные могут принимать только неотрицательные значения, т.е. допустимой областью задачи ЛП (6) - (8) будет область, определяемая условиями (8),(9), или

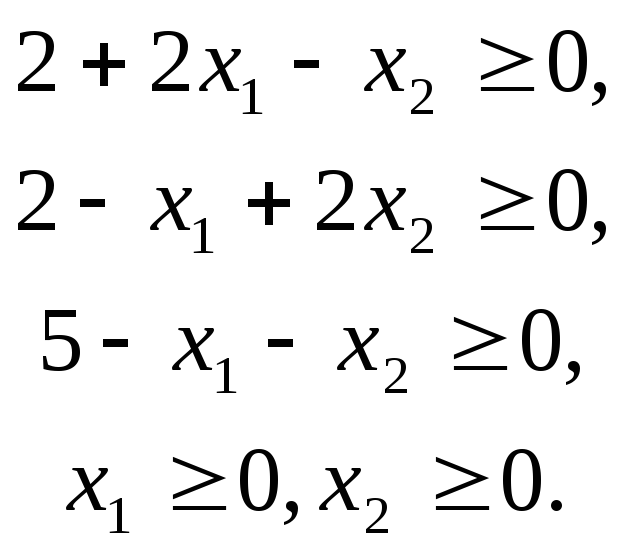(10)

Чтобы получить задачу ЛП относительно переменных x₁,x₂, подставим значения базисных переменных (9) в целевую функцию (6). В результате получим

(11)

Задача (10), (11) эквивалентна задаче (6) - (8), поэтому решая графически задачу (10), (11), получим решение задачи (6) - (8).

Этап 1.Построение допустимой области.

Каждое из неравенств (10) определяет некоторую полуплоскость :

Так, неравенство определяет правую полуплоскость. Неравенствоопределяет полуплоскость, лежащую по ту сторону от прямой, где. Подставляя значенияв это неравенство, получим 0>-2, значит, координаты (0,0) удовлетворяют первому неравенству (10) и область решений этого неравенства включает начало координат. Аналогично определяют полуплоскости остальных неравенств (10).

На рисунке прямые, соответствующие условию , отмечены цифрой в скобках.

Получили допустимую область M– выпуклый пятиугольник OABCD.

Этап 2.В допустимой областиMнаходим оптимальное решение.

Строим прямую и определяем направление возрастания функции, это направление вектора . Перемещая прямуюLпараллельно самой себе в направлении векторадо тех пор, пока она будет сохранять общие точки с областью допустимых решений, найдем, что в крайнем возможном положении прямаяLпройдет через точку. Этому положению прямойLсоответствует значение. Для нахождения координат точкинеобходимо совместно решить систему уравнений граничных прямых, на которых лежит точка:

В результате получаем искомое оптимальное решение . Подставляя значенияив целевую функцию и в равенства (9), получим оптимальное значение целевой функциии оптимальное решение

3. Численные методы решения задач лп

3.1. Симплекс – метод

Рассмотрим задачу ЛП в канонической форме:

(12)

……………………… (13)

(14)

Будем предполагать, что (иначе, умножим соответствующее уравнение на -1), уравнения системы (13) линейно независимы,m<nи система (13) -(14) совместна.

При сделанных предположениях можно выбрать mнеизвестных (к примеру) таких, чтобы определитель, составленный из коэффициентов при этих неизвестных, не обращался в ноль. Тогда задача (12) - (14) может быть приведена к виду, который называетсяспециальной формой задачи ЛП:

…………………………………….. (15)

Одно из допустимых решений этой задачи можно найти, если переменные положить равными нулю. Такое решение называетсядопустимым базисным решением. Оно имеет вид:

Этому решению соответствует значение целевой функции . Переменныеназываютбазисными, набор переменныхназываютбазисом, а переменныеназываютнебазиснымиилисвободными. Число возможных базисов в задаче размерностиnсmограничениями не превосходит величину.

Известно, что каждому допустимому базисному решению соответствует вершина многоугольника допустимых решений и оптимальное решение задачи (при условии его существования) достигается в одной из вершин многоугольника. Поэтому оптимальное решение задачи ЛП находится среди допустимых базисных решений. Существуют рациональные способы последовательного перебора допустимых базисных решений, которые позволяют рассматривать не все допустимые базисные решения, а их минимальное число. К таким методам относится симплекс-метод [1,2,3].