
- •Курсовой проект
- •1 Математическая модель
- •2 Теоретическая часть
- •2.1 Алгоритм метода искусственного базиса
- •2.2 Алгоритм симплекс-метода для задачи на минимум
- •2.3 Алгоритм метода Гомори
- •2.4 Алгоритм двойственного симплекс-метода
- •3 Описание интерфейса программы
- •4 Анализ модели на чувствительность
- •Приложение б результат работы программы
Омский государственный технический университет
Кафедра «Автоматизированные системы обработки информации и управления»
Курсовой проект
по дисциплине «Математическое программирование»
Пояснительная записка
Руководитель проекта:
Зыкина А.В.
Разработал студент гр. Ас–322
Смерницкий Н.М.
Омск - 2005
СОДЕРЖАНИЕ
ЗАДАНИЕ
10. Распределение информации на внешних ЗУ
Рассматривается многоступенчатая система хранения данных: на верхнем уровне используются ЗУ большого объема, обеспечивающим производительность системы.
Пусть n – число массивов информации; di , i=1,n – объем i-го массива информации; Pi , i=1,n – вероятность использования i-го массива в оперативной памяти; m – число уровней памяти; Θj, j=1…m – объем памяти j-го типа; tj, j=1…m – быстродействие памяти j-го типа.
Распределить массивы информации по уровням памяти так, чтобы свести к минимуму время их обработки (суммарное время обращения к памяти).
1 Математическая модель
n – число массивов информации;
di , i=1…n – объем i-го массива информации;
Pi , i=1…n – вероятность использования i-го массива в оперативной памяти;
m – число уровней памяти;
Θj , j=1…m – объем памяти j-го типа;
tj , j=1…m – быстродействие памяти j-го типа (время доступа);
xij – i-й массив находится в j-й памяти {0,1};
Целевая функция.
![]()
Ограничения.
![]() –i-й
массив находится только в одном типе
памяти;
–i-й
массив находится только в одном типе
памяти;
![]()
![]() –общий объем
информации содержащейся в памяти j-го
типа ≤ объема памяти j-го
типа.
–общий объем
информации содержащейся в памяти j-го
типа ≤ объема памяти j-го
типа.
![]()


![]()
Решаем полученную целевую функцию сначала методом искусственного базиса, потом симплекс методом, затем производим решение методом Гомори так как нам нужно получить целочисленное решение.
2 Теоретическая часть
2.1 Алгоритм метода искусственного базиса
Ш1: Приводим задачу ЛП к канонической форме
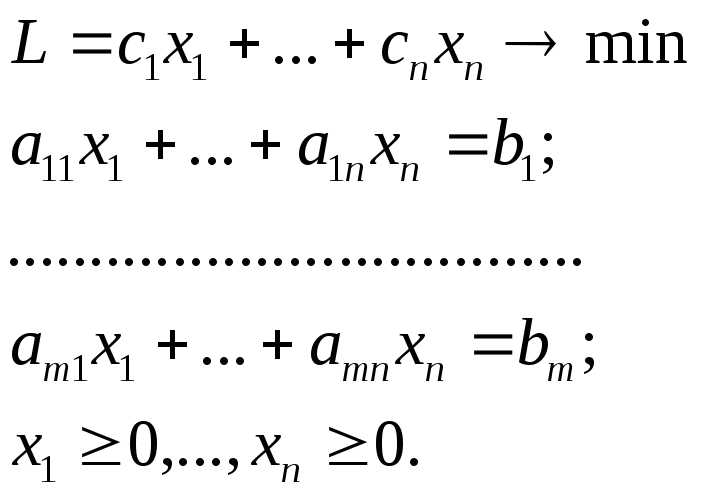
с неотрицательными
правыми частями
![]() .
.
Ш2: В каждую i-ю строку ограничений вводим искусственную неотрицательную переменную xi и строим вспомогательную задачу ЛП вида:

Эта задача имеет
допустимое базисное решение
![]() .
Для этого целевую функцию необходимо
выразить через свободные переменные
.
Для этого целевую функцию необходимо
выразить через свободные переменные![]() :
:
![]()
Ш3: Для построенной вспомогательной задачи строим симплексную таблицу:
|
|
b |
|
… |
|
|
|
|
|
… |
|
|
|
|
|
… |
|
|
. |
. |
… | ||
|
|
|
|
… |
|
и находим оптимальное решение вспомогательной задачи с помощью симплекс-метода.
Ш4:
Если
![]() и все переменные
и все переменные![]() являются небазисными, тоm
переменных из
являются небазисными, тоm
переменных из
![]() войдут в базис и система ограничений,
соответствующих симплексной таблице,
будет иметь вид:
войдут в базис и система ограничений,
соответствующих симплексной таблице,
будет иметь вид:

Так как переменные
![]() ,
то их исключили, не нарушив при этом
равенств. Выражая целевую функцию
основной задачи
,
то их исключили, не нарушив при этом
равенств. Выражая целевую функцию
основной задачи![]() через небазисные переменные
через небазисные переменные![]() системы, получим исходную задачу.
системы, получим исходную задачу.
Ш5:
Если
![]() ,
но в базисе остались искусственные
переменные
,
но в базисе остались искусственные
переменные![]() ,
для которых
,
для которых![]() ,
то проводим для каждой искусственной
переменной
,
то проводим для каждой искусственной
переменной
![]() из базиса следующее преобразование
симплексной таблицы: выбираем ведущим
столбцом столбец такой переменной
из базиса следующее преобразование
симплексной таблицы: выбираем ведущим
столбцом столбец такой переменной
![]() ,
для которой элемент индексной строки
,
для которой элемент индексной строки![]() ,
а элемент столбца
,
а элемент столбца
![]() .
В этом случае строка искусственной
переменной
.
В этом случае строка искусственной
переменной
![]() будет ведущей и после стандартного
преобразования симплексной таблицы
(Ш6 из прямого симплекс-метода) искусственная
переменная
будет ведущей и после стандартного
преобразования симплексной таблицы
(Ш6 из прямого симплекс-метода) искусственная
переменная![]() выведется из базиса. В результате получим
симплексную таблицу, соответствующуюШ4.
выведется из базиса. В результате получим
симплексную таблицу, соответствующуюШ4.
Ш6:
Если
![]() ,
то допустимого решения в исходной задаче
не существует (не могут все искусственные
переменные
,
то допустимого решения в исходной задаче
не существует (не могут все искусственные
переменные![]() быть равными нулю), а значит, система
ограничений задачи несовместна –
процесс решения исходной задачи
завершается.
быть равными нулю), а значит, система
ограничений задачи несовместна –
процесс решения исходной задачи
завершается.
